中国股票市场资产价格模型设定检验

,

(1.上海财经大学经济学院，上海 200433；2.上海财经大学数理经济学教育部重点实验室，上海 200433；3.江西财经大学金融学院，江西 南昌330013)

1 引言

金融学理论和实践用扩散过程描述资产价格连续变化，以布朗运动积分刻画资产价格风险特征，以Poisson跳过程反映信息披露、突发事件、市场失衡等引起的资产价格跳跃变化，形成跳扩散过程。Back[1]证明，无套利市场上资产价格的对数(下文简称资产价格)是特殊半鞅，为采用跳扩散过程描述资产价格提供了金融经济学理论基础，同时也给资产价格的模型设定留下不确定性：任一特殊半鞅过程都可以分解为漂移项(drift)、扩散项(diffusion)和跳过程(jump)，跳过程又可以分解为描述大幅跳跃的有限活跃Poisson跳过程和描述小幅跳跃的无限活跃Levy跳过程[2]。实证研究表明资产价格半鞅成分具有不确定性[3-5]。

Duffie和Pan Jun[6]的研究表明，在利率仿射模型中引入Poisson跳能较好刻画利率的分布特征, Carr等[5]认为采用Levy跳过程给出的期权定价具有更高的准确性，而Hedye和Kou[7]的研究发现，引入Poisson跳能更好地捕捉资产价格分布的厚尾性。随着高频数据的获得，很多研究对资产价的动态特征进行研究。在包含布朗运动积分过程的假设下，Barndorff-Nielsen和Shephard、Jiang和Oomen以及Lee和Mykland的检验表明资产价格包含Poisson跳[8-10]，Lee和Hannig[11]的检验则表明资产价格中存在Levy跳。但这些研究均未涉及资产价格中是否包含布朗运动成分。基于资产价格半鞅成分的重要性以及实证结论的不一致性，Ait-Sahalia和Jacod[12-14]采用非参方法给出了价格成分设定检验的统一框架。

国内对资产价格模型的检验集中在是否存在Poisson跳。陈浪南和孙坚强[15]采用GARCH跳模型对上证综指日数据的实证研究表明，上证综指中的Poisson跳存在时变特征和群集效应，陈国进和王占海[16]采用1分钟高频数据对沪深300指数进行分析，得出资产价格存在Poisson跳的结论，沈根祥[17]、杨科和陈浪南[18]和欧丽莎等[19]对上证综指高频数据的实证研究表明，上证综指存在Poisson跳，并表现出群集特征。沈根祥[20]对沪深300指数5分钟数据进行逐时点Poisson跳检验的结论表明，沪深300指数中的跳服从Poisson过程，刘志东和陈晓静[21]将上证综指直接设定为包含无限活动Levy跳的CGMY过程，并未涉及模型设定的检验。

本文采用Ait-Sahalia和Jacod[12-14]的非参方法对我国股票市场资产价格过程进行设定检验。对资产价格过程中是否存在布朗运动、Poisson跳过程和Levy跳过程进行实证分析。选取上证综指、深证成指和沪深300指数作为研究对象，分析市场微观结构噪音影响，选择10分钟高频数据为样本进行检验，研究结果表明，我国股票市场资产价格过程既包含布朗运动成分，也包含跳过程，既包含有限活动的Poisson跳过程，也包含无限活动的Levy跳过程。由此得出结论：附加无限活动Levy跳过程的跳扩散过程是适合我国股票市场的资产价格模型。本文的研究结果为相关研究提供了基础性的实证结论。

2 资产价格过程的半鞅设定

设时间区间[0,T]内时刻t处的资产价格为Pt，对数价格(以下简称价格)为pt=lnPt。Back[1]证明，无套利市场价格过程pt是特殊半鞅，可以用随机微分方程表示为[2]：

dpt=μtdt+σtdwt+dJt

(1)

μt、σt为适应过程，wt为标准布朗运动。μtdt+σtdwt为资产价格的连续部分。Jt为跳过程，描述资产价格的不连续部分，可以分解为Poisson跳过程和Levy跳过程：

(2)

J1t为Poisson跳过程，描述跳幅(jump size)大于ε的跳，是Poisson计数过程Nt和独立同分布的跳幅随机变量序列{γl}形成的复合Poisson过程，用Poisson随机测度υ(dx,ds)的积分表示。J2t为Levy跳过程，描述跳幅不超过ε的跳，重点描述跳幅接近零的跳发生的情况，通过Levy测度ν(dx)在0邻域内的性质进行刻画。J1t在有限时间区间内跳发生次数(以概率1)有限，是有限活动(finite activity)跳过程，J2t在任一时间区间内都有无限次小幅跳发生，是无限活动(infinite activity)跳过程，即Levy过程的跳密度测度ν(R)=，R为实数域。

半鞅过程的各组成部分描述了资产价格变化的不同情况。扩散过程描述资产价格的正常变化，其中σtdwt度量了布朗运动形成的风险，可以通过标准的方法进行对冲。dJ1t刻画重大信息披露引起的资产价格瞬间大幅跳跃，dJ2t刻画市场失衡、大宗交易等引起的资产价格的小幅跳跃，是与交易策略相关的风险源。除漂移项之外，σtdwt、dJ1t和dJ2t其中之一或者其组合相加都能形成实质性特殊半鞅。模型设定检验的目的，是确定资产价格过程是否包含对应特定资产变化的各种半鞅成分。

设定义随机过程的概率空间为(Ω,F,Ft,P)，Ft为随机过程对应的滤波(filtration)。根据(1)和(2)中给出的分解，将不同假设的样本空间表述为Ω的子集。用Ωw和Ωnow分别表示存在布朗运动成分和不存在布朗运动成分的半鞅集合，Ωc和Ωj分别表示连续半鞅和不连续半鞅形成的集合，Ωf和Ωi分别表示有限活动跳过程和无限活动跳过程的集合。

3 检验统计量构造

设时间段[0,T]等间隔时点{t0,t1,t2…,tn}观测到资产价格p(t0),p(t1),…,p(tn)，其中p(t0)=p0,p(tn)=pT。设Δn表示时间间隔，n→时表示资产价格在区间[ti,ti+1]上的变化i=0,1,…,n，Δpt=pt-pt-表示资产价格在时点t处的改变量，pt-表示价格过程在t处的左极限。如果Δpt=0则表示资产价格在t处连续，否则表示发生了跳跃。设r≥0，定义价格改变量形成的已实现门限幂变差(realize threshold power variation)：

(3)

3.1 布朗运动成分检验统计量

检验资产价格过程是否包含布朗运动成分，有两种方式设定待检验假设：将包含布朗运动成分设为原假设和将不包含布朗运动成分设为原假设。此外还需要设定在不包含布朗运动成分时价格过程包含的其他成分，最一般的设定是价格半鞅包含B-G指数(Levy过程跳发生强度，取值范围是(0,2)[2])β<2的无限活动Levy跳过程，用Ωiβ表示。为此给出两种方法的待检验假设

(1a)H0:Ωw；H1:Ωnow∩Ωiβ；(1b)H0:Ωnow∩Ωiβ；H1:Ωw∩Ωiβ

(1a)将包含布朗运动设为原假设，(1b)将不包含布朗运动设为原假设。

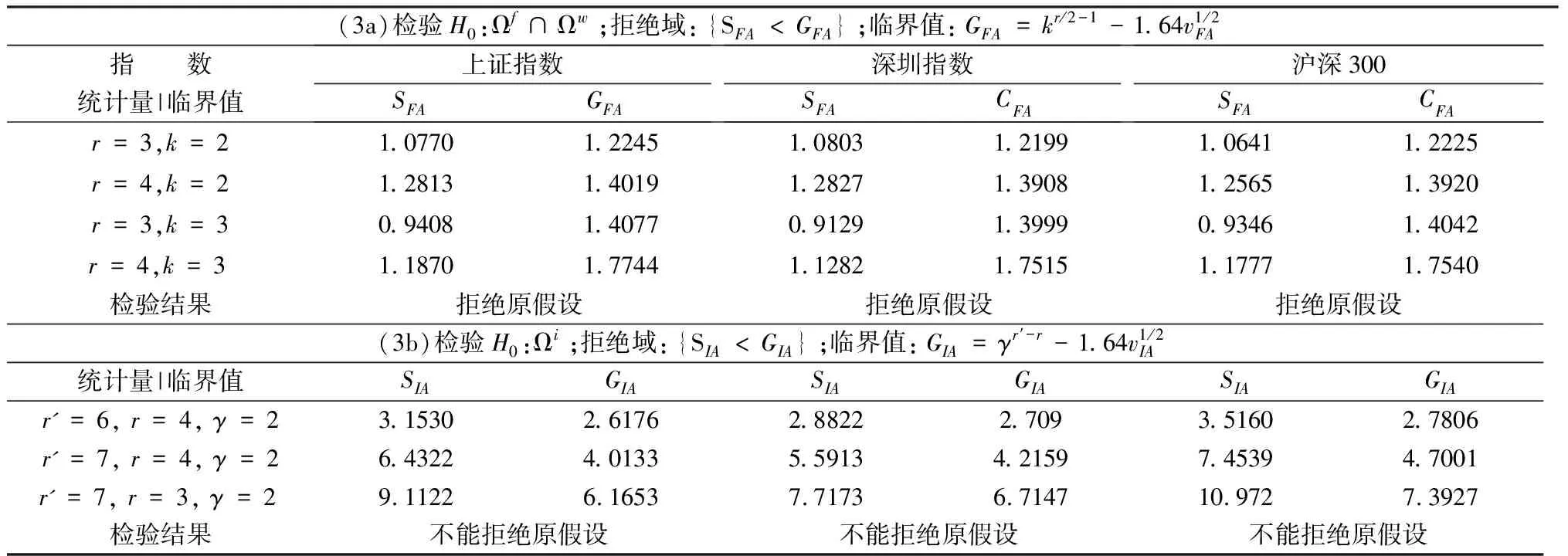
首先考虑待检验假设(1a)的检验统计量构造。在价格半鞅包含布朗运动成分的原假设下，r<2对应的幂变差B(r,un,Δn)主要包含连续扩散过程产生的价格改变量，并且当Δn→0时以概率趋于无限大[22-23]；在不存布朗运动成分而只有无限活动Levy跳成分的备择假设下，当0

(4)

Ait-Sahalia和Jacod[13]给出Sw(1a)原假设的概率极限为k1-r/2，备择假设下的概率极限为1。两个概率极限的巨大差异，使Sw能够有效地区分两种不同类型的模型，并推导出经标准化后Sw在原假设下的极限分布(此处为稳态收敛(stable convergence in law)意义下的极限[13])：

vw为Sw的方差估计量，计算公式为vw=C(r,k)[B(2r,un,Δn)/B2(r,un,Δn)，其中：

U和V为相互独立的标准正态分布随机变量。由此得出显著水平α下(1a)的拒绝域为：

zα为标准正态分布的α分位数(下同)。

由于检验(1a)的第二类错误难以控制，考虑以不存在布朗运动成分为原假设的(1b)的检验统计量构造。不存在布朗运动时，必须假定存在跳过程成分，包括Poisson大幅跳和Levy小幅跳，否则资产价格模型只剩下趋势项而没有风险项，成为无风险资产模型，而只包含Poisson跳过程不能反映资产价格的小幅变化，因此原假设需设为Ωnow∩Ωiβ。(1b)的检验统计量构造主要依赖不同门限阈值下门限二阶变差B(2,un,Δn)的变化。二阶变差(r=2)中布朗运动和跳过程产生的价格改变量同样重要，但通过门限阈值可以去掉B(2,un,Δn)中跳过程价格改变量。如果备择假设成立，un→0时B(2,un,Δn)中只剩下布朗运动价格改变量，将门限阈值改变一个常数倍不会影响这一结论，即取γ>1时B(2,γun,Δn)和B(2,un,Δn)具有相同的极限，二者比值以概率收敛到1。但如果原假设成立，二者的比值的概率极限为γ2-β，由于β未知，无法计算原假设的拒绝域。为消掉β，考虑上截尾幂变差U(0,un,Δn)和U(0,γun,Δn)比值，极限状态下二者都只包含跳产生的幂变差，比值的概率极限为γβ，与二阶变差比值相乘便可消掉β。基于以上分析，定义检验统计量Snow：

(5)

Ait-Sahalia和Jacod[13]证明Snow(1b)原假设下的概率极限为γ2，备择假设下的概率极限为γβ，标准化后Snow的渐进分布为：

vnw为Snow的方差估计量，计算公式为:

vnw=γ4{B(4,un,Δn)/B2(4,un,Δn)+U-1(0,un,Δn)+(1-2/γ2)[B(4,un,Δn)/B2(4,un,Δn)+U-1(0,γun,Δn)]}

由此得出显著水平α下(1b)的拒绝域为：

3.2 跳过程成分检验统计量

与布朗运动成分检验一样，检验资产价格过程是否包跳过程有两种方式设定待检验假设：包含跳过程设为原假设和不包含跳过程为原假设。在不存在跳的情况下，需要假设价格过程包含布朗运动成分。为此给出两种方式的待检验假设

(2a)H0:Ωj；H1:Ω∩Ωw； (2b)H0:Ωc∩Ωw；H1:Ωj

(2a)的原假设为包含跳过程，(1b)的原假设为不包含跳过程。

首先考虑(2a)的检验统计量构造。设B(r)=∑sT|Δsp|r为价格过程的r阶跳变差。根据变差理论，当r>2时半鞅过程的r阶变差中连续扩散部分形成的r阶变差为0，等于r阶跳变差B(r)。如果价格过程包含跳过程，当Δn→0时B(r,Δn)和较低抽样频率下的B(r,kΔn)(k≥2)都以概率收敛到B(r)，如果价格过程为布朗运动形成的连续过程，两者具有不同的概率极限。基于上述分析，定义检验统计量SJ

(6)

Ait-Sahalia和Jacod[12]证明SJ在(2a)原假设下概率极限为1，备择假设下概率极限为kr/2-1，当r>3时，标准化后SJ的渐进分布为：

vJ为原假设下SJ的方差估计量，计算公式为vJ=[(k-1)Δnr2D(r,Δn)]/[2B2(r,Δn)]，其中:

由此得出显著水平α下(2a)的拒绝域为：

检验假设(2b)的统计量与检验(2a)的检验统计量相同，即SJ。Ait-Sahalia和Jacod[12]证明在(2b)原假设下，当r>2时，标准化后SJ的渐进分布为：

由此得出(2b)的拒绝域为

需要注意的是，(2b)原假设下SJ的概率极限kr/2-1>1，而备择假设下的概率极限是1，因此原假设拒绝域是临界值Cc的左侧区域。

3.3 Levy跳成分检验统计量

与前两种检验一样，有两种方式设定待检验假设：不包含Levy跳过程(但包含Poisson跳过程和布朗运动成分)作为原假设和包含Levy跳过程作为原假设。两种方式的待检验假设为：

(3a)H0:Ωf∩Ωw;H1:Ωi; (3b)H0:ΩiH1:Ωf∩Ωw

首先考虑(3a)的检验统计量构造。(3a)原假设假定价格过程只包含大幅Poisson跳，而备择假设假定还包含跳幅可以任意小的Levy跳。采用不同抽样频率下r>2的门限幂变差构造检验统计量。由于Poisson大跳的跳幅不随Δn变化，采用门限值进行截尾，可以将其从幂变差中去掉。因此，如果价格过程只包含Poisson跳和布朗运动成分(即原假设成立)，不同抽样频率下的截尾幂变差B(r,un,kΔn)(k≥2)和B(r,un,Δn)在Δn趋于0时只包含布朗运动成分产生的价格改变量，其比值的概率极限为kr/2-1。如果价格过程包含跳幅可以任意小的Levy跳，则不管Δn多小，门限幂变差中都包含Levy跳产生的价格改变量。根据布朗运动的性质，r>2的门限幂变差中主要成分是Levy跳产生的价格改变量，因此B(r,un,kΔn)和B(r,un,Δn)具有相同的概率极限，其比值的概率极限为1。基于以上分析，定义检验统计量SFA：

(7)

Ait-Sahalia和Jacod[14]证明在(3a)原假设下，标准化后SFA的渐进分布为：

vFA为SFA的方差估计量，计算公式为：

vFA=C(r,k)B(2r,un,Δn)/B2(r,un,Δn)

由此得出(3a)的拒绝域为：

(3b)的检验计量构造较为复杂，原假设下价格过程包含无限活动的Levy跳过程，需要采用不同次幂的幂变差和不同截尾阈值的幂变差构造检验统计量才能区分原假设和备择假设。定义检验统计量SIA：

(8)

在原假设下价格过程中包含跳幅可以任意小的Levy跳，当Δn→0时SIA中幂变差以不同的阶数趋于0，即：

B(r′,γun,Δn)=Op((γun)r′-β)

B(r,γun,Δn)=Op((γun)r-β)

vIA为SIA的方差估计量，计算公式为：

vIA=γ2(r′-r){B(2r,un,Δn)/B2(r,un,Δn)+(1-2γ-r)B(2r,γun,Δn)/B2(r,γun,Δn)+B(2r′,un,Δn)/B2(r′,un,Δn)+(1-2γ-r′)B(2r′,γun,Δn)/B2(r′,γun,Δn)-2B(r′+r,un,Δn)/[B(r′,un,Δn)B(r,un,Δn)]-2(1-γ-r-γ-r')B(r′+r,γun,Δn)/[B(r′,γun,Δn)B(r,γun,Δn)]}

由此得出(3b)的拒绝域为：

4 资产价格模型设定的实证检验

4.1 数据说明

本文选取代表我国股票市场资产价格的上证指数、深圳成指、沪深300进行实证分析，抽样范围为2010.01.04至2010.12.31的，样本为日内高频数据，数据来源为《天相投资数据库》。研究发现，金融高频数据中存在微观市场结构噪音，如买卖价差、价格离散等，对幂变差的估计及其概率极限产生影响，抽样频率越高，噪音的影响越严重[26]。减少噪音影响的方法之一是降低抽样频率。采用已实现方差图示法选择数据抽样频率，发现抽样频率低于8分钟后已实现方差趋于稳定。图1给出的是沪深300指数平均已实现方差随抽样频率变化的趋势图，其它两个指数具有类似的情况。据此，本文选取10分钟的高频数据作为实证分析样本，抽样区间内共有5808个有效样本。设抽样区间为[0,1]，则n=5808，Δn=1/n=0.00017。

4.2 模型设定检验

4.2.1 布朗运动成分检验

4.2.2 跳过程检验

表1 布朗运动成分检验结果

(1a)检验结果表明，统计量样本值Sw显著大于拒绝域临界值Dw，在5%显著水平下不能拒绝价格过程包含布朗运动成分的原假设，并且取r和k的不同值时检验结果不发生变化。(1b)检验结果表明，统计量样本值Snow显著小于拒绝域临界值Dnow，在5%显著水平下拒绝价格过程不包含布朗运动成分的原假设，并且γ取不同值时检验结果不发生变化。由此得出结论，上证指数、深圳成指、沪深300存在布朗运动成分。

表2 跳过程成分检验结果

显著性水平下(2a)原假设H0:Ωj为拒绝域为

从检验结果看出，5%显著水平下不能拒绝(2a)的资产价格过程包含跳过程的原假设，能够拒绝(2b)的资产价格过程不包含跳过程的原假设。检验结果对r和k的取值具有稳定性。由此表明，上证指数、深圳成指、沪深300存在跳过程成分。

4.2.3 Levy跳检验

表3 Levy跳过程成分检验结果

5 结语

采用基于高频数据非参数统计检验的实证分析表明，以上证指数、深证综合指数和沪深300指数为代表的中国股票市场资产价格过程，包含布朗运动成分、Poisson跳成分和Levy跳成分，是典型的特殊半鞅过程。扩散过程、跳扩散过程、纯跳过程都不能完全刻画中国股票市场资产价格的动态变化，必须引入具有无限活动的Levy跳过程。

本文采用日内10分钟高频数据作为实证样本，有效减少市场微观结构噪音的影响，每个检验都采用原假设和备择假设互换两种方法进行，控制了两类错误，对同一原假设下的检验统计量取不同参数值进行多次检验以保证稳定性。所有情况下得出了相同的检验结果，实证结论具有可信性。

参考文献：

[1] Back K.Asset pricing for general processes[J].Journal of Mathematical Economics, 1991, 20(4):371-395.

[2] Protter P.E.Stochastic Integration and Differential Equations[M].Berlin: Springer，2004.

[3] Bates D.Post-’87 crash fears in the S&P500 futures option market[J].Journal of Econometrics, 2000, 94(1-2):181-238.

[4] Eraker B，Johannes M，Polson N.The impact of jumps in equity index volatility and returns[J].Journoal of Finance, 2003, 58(3):1269-1300.

[5] Carr P，Geman H，Madan D，B，et al.The fine structure of asset returns: An empirical investigation”[J].Journal of Business, 2002, 75: 305-332.

[6] Duffee D, Pan Jun.Analytical value-at-risk with jumps and credit risk[J].Finance and Stochastics, 2001,5(2):155-180.

[7] Heyde C, Kou G.On the controversy over tailweight of distributions[J].Operation Research Letters, 2004, 32(5):399-408.

[8] Barndorff-Nielsen O E, Shephard N.Econometrics of testing for jumps in financial economics using bipower variation[J].Journal of financial Econometrics, 2006, 4(1):1-30.

[9] Jiang G J, Oomen R C A.Testing for jumps when asset prices are observed with noise - A "swap variance" approach[J].Journal of Econometrics, 2008, 144(2): 352-370.

[10] Lee S S.Mykland P.A.Jumps in financial markets: A new nonparametric test and jump dynamics[J].Review of Financial Studies, 2008, 21(6):2535-2563.

[11] Lee, S.S.Hannig J.Detecting jumps from Lévy jump diffusion processes[J].Journal of Financial Economics, 2010, 96(2):193-215.

[12] Aït-Sahalia Y, Jacod J.Testing for jumps in a discretely observed process[J].Annals of Statistics, 2009, 37(1): 184-222.

[13] Aït-Sahalia Y, Jacod J.Is Brownian motion necessary to model high frequency data?[J].Annals of Statistics, 2010,38(5):3093-3128.

[14] Aït-Sahalia Y, Jacod J.Testing whether jumps have finite or infinite activity[J].Annals of Statistics, 2011, 39(3):1689-1719.

[15] 陈浪南，孙坚强.股票市场资产收益的跳跃行为研究[J].经济研究, 2010, 4:54-66.

[16] 陈国进，王占海.我国股票市场连续性波动与跳跃性波动实证研究[J].系统工程理论与实践，2010, 9:1554-1562.

[17] 沈根祥.沪深300指数日内跳的Hansman检验[J].数理统计与管理，2010, 4:713-718.

[18] 杨科，陈浪南.基于C-TMPV的中国股市高频波动率的跳跃行为研究[J].管理科学, 2011, 2:103-112.

[19] 欧丽莎，袁琛，李汉东.中国股票价格跳跃实证研究[J].管理科学学报，2011, 14(9):60-66.

[20] 沈根祥.沪深300指数跳的逐点检验及动态分析[J].中国管理科学，2012，20(1):43-50.

[21] 刘志东，陈晓静.无限活动纯跳跃Levy金融资产价格模型及其CF-CGMM参数估计与应用[J].系统管理学报,2010, 4:428-438.

[22] Barndorff-Nielsen O E，Shephard N，Winkel M.Limit theorems for multipower variation in the presence of jumps[J].Stochastic Processes and Their Applications, 2006, 116:796-806.

[23] Barndorff-Nielsen O E，Graversen E，Jacod J，et al.A central limit theorem for realized power and bipower variations of continuous semimartingales[M].Berlin: Springer, 2006.

[24] Mancini C.Non-parametric threshold estimation for models with stochastic diffusion coefficient and jumps[J].Scandinavian Journal of Statistics, 2009,36:270-296.

[25] Karatzas I, Shreve S E.Brownian motion and stochastic calculus[M].Berlin:Springer, 1991.

[26] Hansen P R, Lunde A.Realized variance and market microstructure noise[J].Journal of Business and Economic Statistics, 2006, 24(2):127-161.

[27] Huang Xin, Tauchen G.The relative contribution of jumps to total price variance[J].Journal of Financial Econometrics, 2005, 3(4):456-499.