TMD对列车作用下大跨钢桁架桥的振动控制研究

王 浩， 刘海红， 陶天友， 宗周红, 何旭辉

(1.东南大学混凝土及预应力混凝土结构教育部重点实验室， 江苏 南京 210096；2.中南大学土木工程学院， 湖南 长沙 410082)

引 言

南京长江大桥于1968年通车运营，是长江上第一座由中国自行设计建造的公铁两用的特大桥梁，具有重要的历史和现实意义。因为南京长江大桥为钢桁架结构，桁架桥梁在列车荷载作用下振动普遍比较的剧烈，故由列车所引起的振动不仅对桥梁结构本身造成巨大的危害，还影响列车行驶过桥时乘客的舒适感[1]。鉴于南京长江大桥的重要地位，有必要进行该桥的减振研究，通过减小由列车荷载引起的桥梁结构竖向振动来延长大桥使用寿命，降低其维护管理费用，提高列车的乘坐舒适度。显然，本研究经济社会效益重大。

调谐质量阻尼器(TMD)是一种被广泛应用的动力减振器，1909年由美国的Frahm率先提出。由于TMD具有经济、方便、抑制窄带振动效果显著等优点，近年来被广泛应用于桥梁结构振动控制中，并在大量实际工程领域取得了良好的减振效果。Gu Ming对比研究了采用半主动式TMD的一座悬索桥的风致振动的控制效果[2]；曾宪武通过对斜拉桥的抖振控制分析，研究了模态间气动耦合效应对TMD最优参数和控制效率的影响；Miguel Moura Paredes等、霍林生等、樊健生等研究了TMD对人行天桥由行人引起振动的控制作用[4～6]；Yung-Hsiang Chen分析了TMD对Timoshenko梁在移动荷载下的减振效果[7]；肖新标等研究了移动荷载下桥梁的振动机理与TMD减振控制[8]；Kwon等分析了TMD对高速铁路连续梁桥的振动控制效果[9]；李建中通过TMD-桥梁-车辆系统动力方程对TMD抑制钢桥的竖向共振的振动效果进行了理论分析[10]；顾萍等分析了MTMD抑制铁路钢桁梁桥横向振动的振动效果[11]；Lin等结合理论和数值模拟计算了采用优化MTMD的高速铁路桥梁的动力响应[12]；彭献等通过建立安装TMD前后的车桥耦合系统的动力模型，研究了车辆变速、桥面粗糙度等对系统振动的影响[13]。但是已有的研究大都集中在TMD对桥梁风振的控制，以及考虑移动荷载作用下的人行天桥或梁桥的TMD控制，目前尚未见到TMD抑制大跨度钢桁架桥梁的车致振动方面的文献发表。

考虑到有阻尼TMD可用于激振频率较宽的频带范围，本文以南京长江大桥为工程实例，尝试将有阻尼TMD装置应用于大桥的减振控制中，首先将列车匀速经过全桥过程中的桥梁结构简化为时变系统，基于ANSYS的瞬态动力时程分析，然后主要研究了TMD的刚度和阻尼系数的参数敏感性，最后对比了在不同列车时速下TMD对该桥的减振效果。

1 工程概况

1.1 南京长江大桥简介

南京长江大桥位于中国铁路南北通道京沪干线和公路干线宁杨国道上，其整体立面布置见图1。该桥于1968年10月1日铁路通车，12月29日公路通车。上层公路桥长4 588 m，其中主桥1 576 m，四车道，总宽为19.5 m；下层铁路桥长6 772 m，宽14 m，两线铁路中心距为4 m。主桥为钢桁架结构，共9墩10孔(1孔128 m的简支梁+3联9孔各160 m的连续梁)，每个墩高80米。主桁为平弦菱形桁，节间8 m，桁高16 m，下加劲桁弦高14 m；两主桁中心距为14 m。主桁及铁路横梁等主要结构用16Mnq低合金钢，钢梁以铆接为主，铺设无缝钢轨。大桥南北各有一对高10 m的桥头堡。

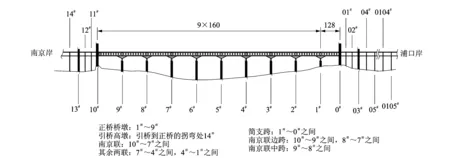
图1 南京长江大桥立面布置图(单位：m)

1.2 有限元建模

图2 南京联主桁三维有限元模型

该桥主桁杆件有30种不同截面，众多类型的纵横向连接系以及铁路、公路两种不同桥面系等，结构十分复杂。本文选取南京联主桁进行分析，该联的有限元模型如图2所示，其中共有7 960个单元，5 227个节点。模型中的单元选取如下：主桁杆件、铁路纵梁、横梁、上下平横向连接系等采用三维梁单元Beam4，公路纵梁、公路桥面混凝土以及铁路混凝土轨枕、无缝钢轨等对结构刚度贡献较小的部分简化为质量单元Mass21加在上、下平联的相关节点上。为了便于施加列车轮轴轴力，网格划分时对纵梁进行了局部细化。对4个支撑处都施加竖向、绕竖向和横向转动约束，对中跨的两个支撑施加纵向约束，4个支撑处在同一侧分别选取一个支撑点进行横向约束。

1.3 动力特性

基于上述有限元模型，采用子空间迭代法进行了模态分析。前10阶频率值和振型特点见表1。考虑到本研究主要针对竖弯振型进行TMD控制，列出了前2阶竖弯振型，见图3。

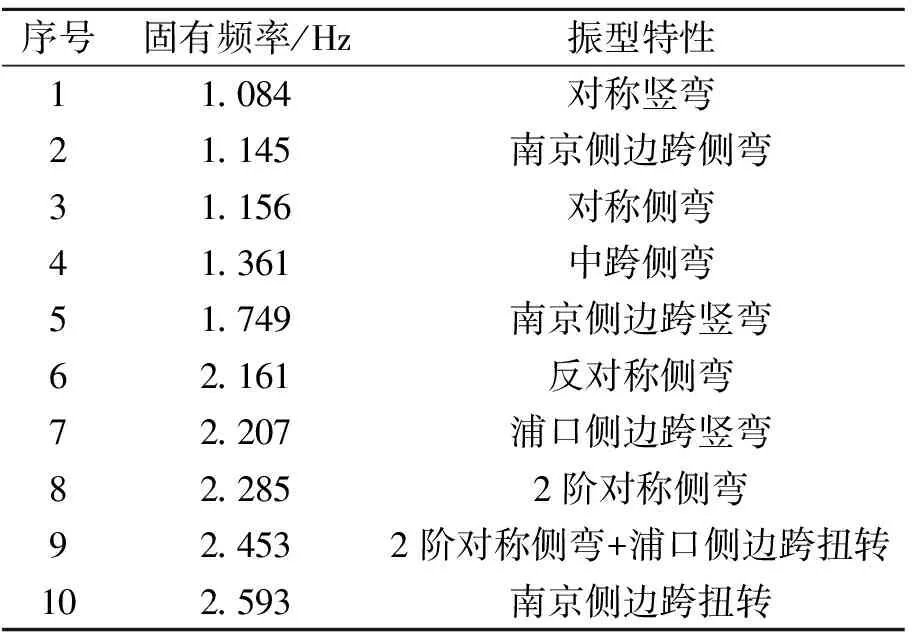
表1 南京联主桁动力特性

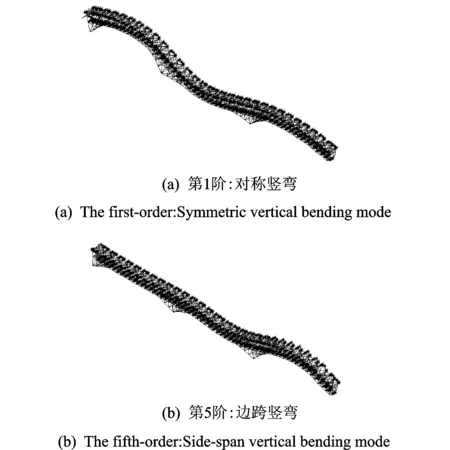
图3 竖弯振型图

表1表明：由于该桥较大的宽跨比，该桥侧向刚度相对较大，使得其第1阶振型为竖向对称弯曲振型，侧弯振型到第2阶之后出现，说明该桥的竖向振动值得引起注意。

2 时变系统分析

2.1 时变系统的理论模型

车辆-桥梁耦合系统的动力特性随荷载位置的移动而不断变化，其结果是共振条件只能在短时间内满足，并且车辆荷载在桥上通过的时间也是有限的。这是桥梁的车辆激振问题的特点和复杂性所在，给理论分析带来了极大的困难[14，15]。为此，本文采用了简化的时变系统理论模型[16，17]。简支梁在外荷载p(x,t)作用下的振动方程可表示为

(1)

式中EI为梁的抗弯刚度，假定为常数；m为梁单位长度上的质量，亦假定为常数；且暂不计梁的阻尼影响。设梁强迫振动的动位移y(x,t)可表示为振型的级数形式

(2)

式中φn(x) 为第n阶振型，qn(t)为相应的模态坐标。解耦后的强迫振动方程为

(3)

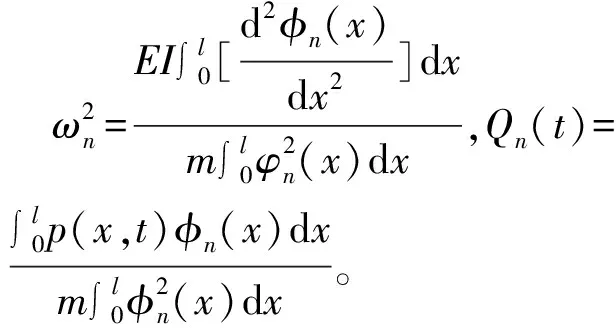
对于简支梁，有

(4)

因此，对移动的常量力F匀速通过简支梁的情况，如图4所示。

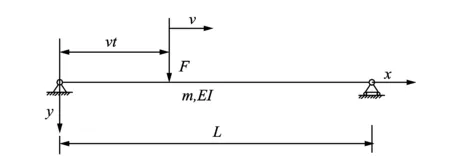
图4 匀速移动常量力作用于简支梁的模型

图4中，假设在时间t=0时，F位于左边支承处；在时间t时，常量力F将移动到距左边支承点x=vt处。此时广义激扰力为

(5)

于是，式(3)可写成

(n=1,2,3,…,N)

(6)

当初始条件为静止时，可得上式的解为

(7)

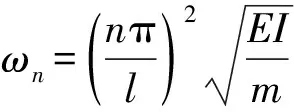
(8)

式(8)表明动力响应包括两部分中，括号的前一项代表强迫振动，后一项为自由振动。

2.2 时变系统的有限元模拟及其在ANSYS中的实现

考虑到列车荷载作用相对汽车荷载较大，这里仅将南京桥健康监测系统实测的列车荷载作为激振力，对理论模型进行动力时程分析。为了便于计算，在ANSYS对移动荷载的模拟中，把列车全过程经过大桥的桥梁结构简化为时变系统：利用实测的列车活载的轴数、轴重、轴距及行车速度的数据，首先定义列车轴重、列车轮轴轴力数组，然后将轴重作为质量单元加在在南京联主桁纵梁节点上，将轴力作为一列匀速移动的集中荷载作用在简支跨主桁纵梁相应节点上，再在APDL中利用IF语句来判断列车到达不同主桁纵梁节点的时刻，通过单元生死法激活相应节点处的列车质量单元及集中荷载，从而实现列车匀速经过全桥的时变系统模拟。文献[15]采用实测结构响应对本分析方法的可靠性进行了验证。

3 TMD的减振效果分析

3.1 TMD的设置

TMD装置用于桥梁的振动控制时，首先需要考虑移动荷载的激励频率范围，然后估算桥梁最大挠度发生的位置，在此位置上安装TMD装置。在ANSYS中，TMD采用弹簧阻尼器单元Combin14来模拟，TMD的质量简化为质量单元Mass21。TMD减振效果随着质量比的增加更加显著，但是当质量比超过一定范围后其减振效果反而会变差。因为TMD质量越大，其动力消振作用越大，同时桥梁静挠度也会加大，当TMD质量增大到一定数值时，其动力消振效果比不上其引起的静挠度效果，这时减振效果反而变差。本文采用Den-Hartog的最佳参数调整方法[16，17]:

(9)

式中c和cc分别是TMD的阻尼系数和临界阻尼系数，X1为结构待控制基频，Xz为TMD最佳自振频率，TMD与桥梁的质量比Lz通常在0.01～0.04之间取值，这里取Lz=0.03，M0为桥梁质量，M为TMD质量(取为1 t)，计算得TMD的总数N=36，在跨中处安装TMD。为了分析TMD对桥梁静挠度的影响，分别选三跨主桁的跨中上弦杆的3个节点621，641，661为研究对象，对比其在静载作用下，安装TMD前、后这两种工况下的竖向位移，分析结果见表2。

表2表明，安装TMD前、后这两种工况下，南京联主桁在自重作用下的静力位移变化不大，位移变化率均在10%以内，据此初步判定所选TMD质量及数量合适。

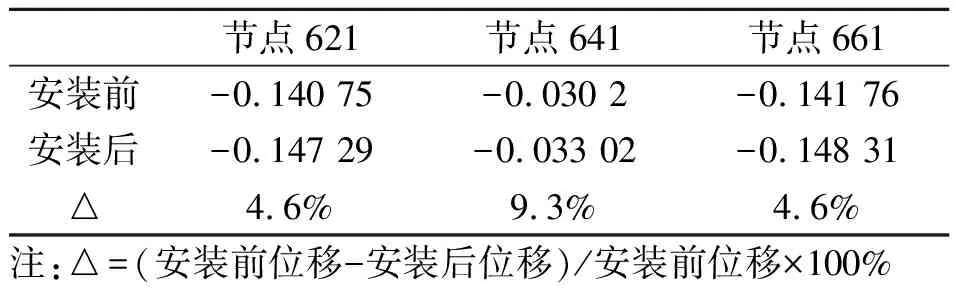
表2 两种工况下静力位移对比/m

3.2 参数敏感性分析

刚度K与阻尼系数C是TMD装置的两个最重要的参数，为了研究TMD用于大跨度钢桁架桥梁的列车致振动的最优控制效果，首先分别对刚度和阻尼系数进行参数敏感性分析。考虑加速度是反映列车振动特性和乘坐舒适度的主要指标，这里选取竖向加速度响应作为主要分析对象。分析时，结构阻尼比取0.05，K的变化范围为20～6 000 kN/m(C设为180 kN·s/m)，C的变化范围取40～800 kN·s/m(K设为800 kN/m)，结果见图5。

需要说明，不设TMD时，节点621，641和661的加速度峰值分别为2.277，2.190和1.764 m/s2，见图6。与图5的对比验证了TMD用于控制该桥列车致振动控制的全面有效性。图5还表明，随着K的增加，节点621和节点661的竖向加速度先减少后增大，而节点641呈现单调增加。在K为800 kN/m左右时，两边跨的竖向加速度接近最低，而中跨的加速度相对于不设TMD时也大为下降，综合考虑可认为800 kN/m为最优K值。类似地，随着C的增加，节点621和节点661的竖向加速度也都先减少后增大，而节点641呈现单调增加。当C为200 kN·s/m左右时，边跨的加速度接近最低，可认为此时为最优C值。

3.3 控制效果对比分析

根据参数分析，选取TMD的K和C分别为800 kN/m和200 kN·s/m，对比两种工况下结构的竖向加速度时程曲线，见图6。其中列车以60 km/h的速度匀速行驶，考虑到前15 s列车刚上桥，结构振动响应较小，46.14 s后列车全部下桥，故选取15～46.14 s进行分析。

图6更加直观地显示了该桥安装TMD后，所选节点在不同时刻的竖向加速度响应和下降程度。为了进一步分析TMD减振效果及对该桥的频率控制范围，基于Matlab平台中的Pwelch函数对以上加速度时程进行功率谱分析，结果如图7所示。

图7的功率谱对比可知：1)安装TMD后，该桥的竖向加速度谱的峰值远小于安装前，表明TMD装置限制了峰值对应的卓越频率对结构振动的贡献，起到了大幅度减小结构振动的作用；2)安装TMD后，该桥竖向加速度谱的峰值总体减小，其中在10～16 Hz频带范围内TMD对结构振动实现了有效的控制，这主要是由于设计TMD的自振频率为14.24 Hz，加上TMD阻尼的影响，使得TMD自振频率附近的结构竖向加速度谱峰值均下降。

3.4 时速影响分析

由动力方程可知，列车时速对桥梁结构的振动影响很大。为了研究列车时速对减振效果的影响，参考实际情况选取列车在40～120 km/h范围内的5种不同时速，对该大桥在两种工况下的竖向加速度进行对比分析。其中均按照前述分析布设TMD装置，见表3。

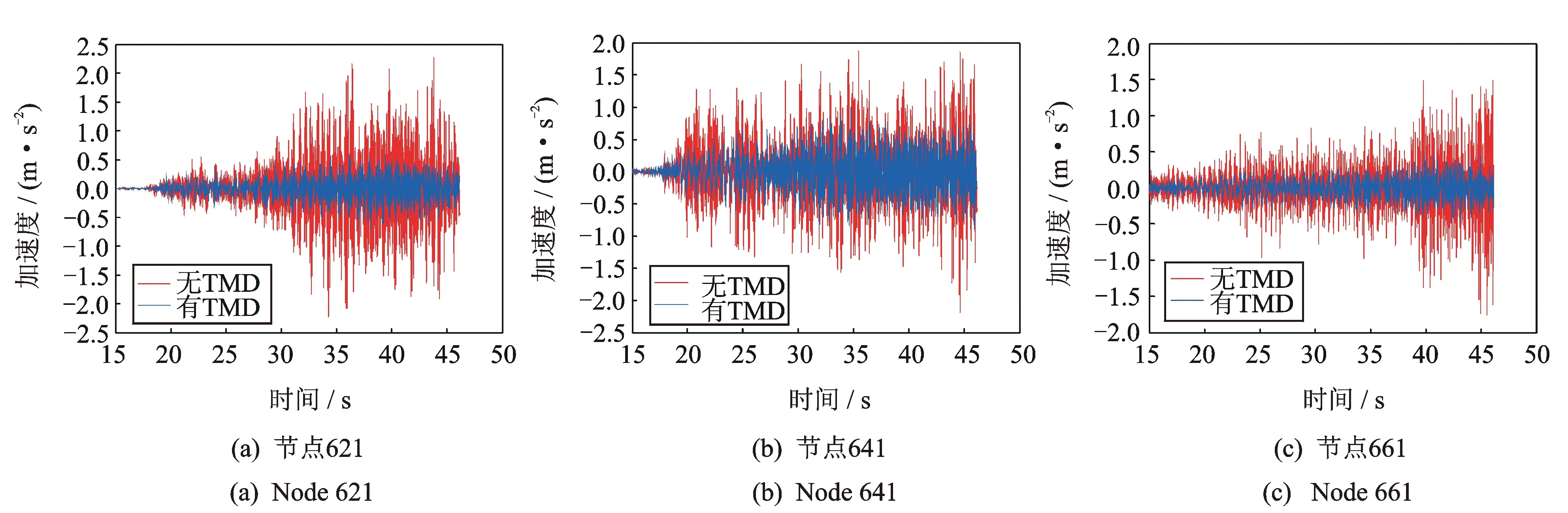
图6 两种工况下竖向加速度时程响应对比

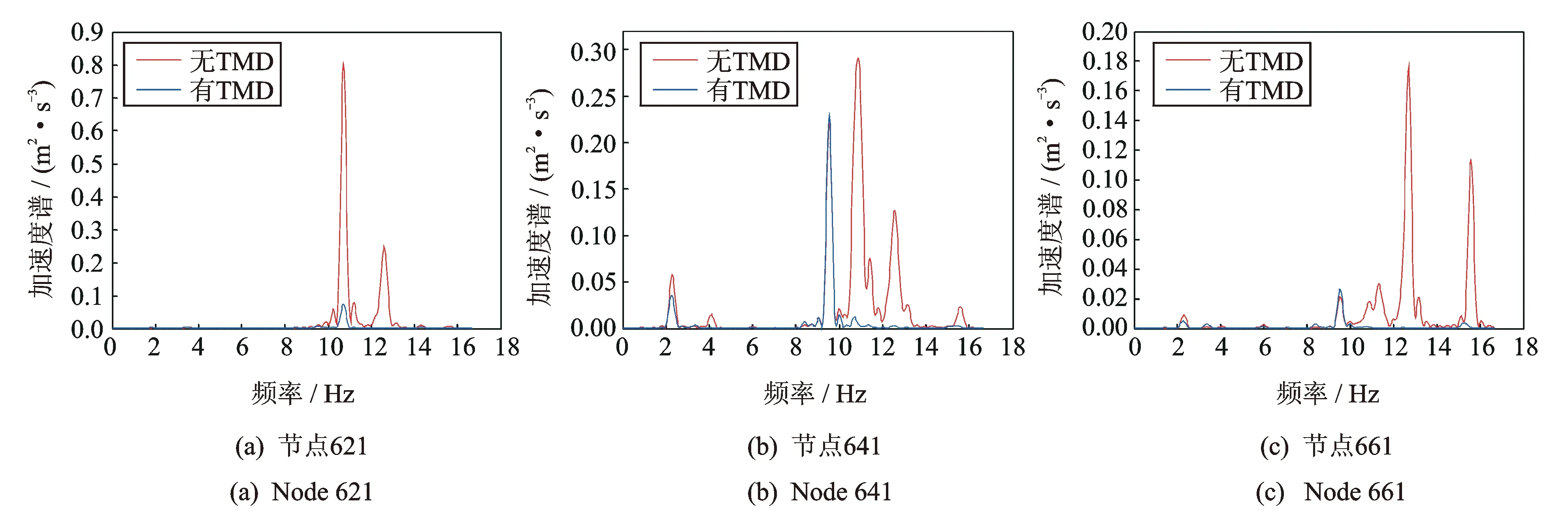
图7 两种工况下竖向加速度功率谱对比

表3 不同列车时速时的减振效果对比/(0.1 m·s-2)

由表3可知，车速越大，大桥的振动响应越大，且振动响应增大的幅度也随着车速的提高而明显加大。在5种不同列车时速下，TMD对南京长江大桥的竖向振动的控制效果都非常明显，南京联主桁结构的竖向加速度均减少了54%以上；而且随着车速的增加，减少率也基本有增大的趋势，当列车时速高达120 km/h时，加速度减少率可达到90%以上。表明当列车处于较高时速运行时的减振效果更加显著。

4 结 论

对大跨度钢桁架桥梁进行列车致振动控制研究具有重要意义。以南京长江大桥为背景，进行了TMD装置应用于列车荷载作用下该桥的减振控制研究，得到以下结论：

1)列车作用下南京长江大桥的振动加速度响应较大，在车速较大时振动更为明显。为了改善大桥的使用性能，提高列车的乘坐舒适度，有必要采取有效措施进行减振控制。

2)安装TMD后，大桥关键部位的列车致竖向加速度响应在相应频段内大幅度下降。且当TMD和结构的质量比Lz=0.03时，TMD在刚度接近800 kN/m、阻尼系数为200 kN·s/m左右时的控制效果最好。

3)功率谱分析结果表明，对于大跨度钢桁架桥梁而言，针对列车致振动专门设计的TMD系统能够在其自振频率周围较宽频带范围内对结构振动进行有效控制。

4)在不同列车时速下，TMD对南京长江大桥竖向加速度的控制效果都非常明显，当时速较高时，TMD对该桥的减振效果更为显著。

参考文献：

[1] Jianzhong Li, Mubiao Su, Lichu Fan. Vibration control of railway bridges under high-speed trains using multiple tuned mass dampers[J]. Journal of Bridge Engineering，2005, 10(3): 312—320.

[2] M Gu, S R Chen, C C Chang. Control of wind-induced vibrations of long-span bridges by semi-active lever-type TMD[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2002, 90(2):111—126.

[3] 曾宪武, 韩大建. 模态间期待耦合效应对调谐质量阻尼器最优参数的影响[J]. 土木工程学报, 2005, 38(11): 64—68.Zeng Xianwu, Han Dajian. Effects of aerodynamic coupling among modes on the optimal parameters of tuned mass damper[J]. China Civil Engineering Journal, 2005, 38(11): 64—68.

[4] Miguel Moura Paredes, Rui Carnriro de Barros. On the use of TMDs for regular buildings and bridges under dynamic actions[A]. AIP Conference Proceedings[C]． 2010, 1 233: 1 624—1 629.

[5] 霍林生, 李宏男. 大跨人行过街天桥利用MTMD减振控制的理论分析[J]. 防灾减灾工程学报, 2008, 28(3): 298—302．Huo Linsheng, Li Hongnan. Theoretical analysis of vibration control of large-span pedestrian bridge by use of MTMD[J]. Journal of Disaster Prevention and Mitigation Engineering, 2008, 28(3):98—302.

[6] 樊健生, 李泉, 聂建国. 人群激励下梁式人行桥振动控制和MTMD优化设计[J]. 土木工程学报, 2010, 43 (8): 73—80.Fan Jiansheng, Li Quan, Nie Jianguo. Crowds-induced vibration control of beam footbridge equipped with multiple tuned mass dampers[J]. China Civil Engineering Journal, 2010, 43(8):73—80.

[7] Yung-Hsiang Chen,Ding-Shin Chen.Timoshenko beam with tuned mass damper to moving loads[J]. Journal of Bridge Engineering, 2004, 9(2): 167—177.

[8] 肖新标, 沈火明. 移动荷载作用下的桥梁振动及其TMD控制[J]. 振动与冲击, 2005, 24(2): 58—61.Xiao Xinbiao, Shen Huoming. Vibration and the TMD control of bridges under moving loads[J]. Journal of Vibration and Shock, 2005, 24(2): 58—61.

[9] Ho-Chul Kwon, Man-Cheol Kim, In-Won Lee. Vibration control of bridges under moving loads[J]. Computers & Structures, 1998, 66(4):473—480.

[10] 李建中, 扬益谦, 苏木标. TMD抑制既有钢桥提速时发生振动的研究[J]. 铁道学报, 1999, 21(1):81—85．Li Jianzhong, Yang Yiqian, Su Mubiao. Suppression of Vibration of Steel Bridges under Speed-up Trains with Tuned Mass Dampers[J]. Journal of the China Railway Society, 1999, 21(1):81—85.

[11] 顾萍, 王淼, 吴定俊, 等. TMD抑制既有铁路钢桁梁桥横向振动研究[J]. 铁道学报, 2005, 2(27): 85—89. Gu Ping, Wang Miao, Wu DingJun, et al. Damping suppression of lateral vibration of the existing steel truss railway bridges using TMD[J]. Journal of the China Railway Society, 2005, 2(27):85—89.

[12] C C Lin, J F Wang, B F Chen. Train-induced vibration control of high-speed railway bridges equipped with multiple tuned mass dampers[J]. Journal of Bridge Engineering, 2005,4(10):398—414.

[13] 彭献, 殷新锋, 方志. 变速车辆与桥梁的耦合振动及其TMD控制[J]. 湖南大学学报(自然科学版), 2006, 33(5): 61—66.Peng Xian,Yin Xinfeng, Fang Zhi. Vibration and TMD control of coupled system of girder bridge and vehicle with variable speeds[J]. Journal of Hunan University(Natural Sciences), 2006,33(5):61—66.

[14] 夏禾. 车辆与结构动力相互作用[M]. 北京: 科学出版社, 2002.Xia He. Dynamic Interaction between Vehicles and Structures [M]. Beijing: Science Press, 2002.

[15] 曾储惠. 南京长江大桥健康监测和状态评估的研究[D].长沙:中南大学,2004.Zeng Chuhui. Research on safety monitoring and Condition assessment of the Nanjing Yangtze River bridge[D]. Changsha: Central South University, 2004.

[16] Chatterjee P K, Datta T K, Surana C S. Vibration of continuous bridges under moving vehicles[J]. Journal of Sound and Vibration, 1994, 169(5): 619—632.

[17] Masato Abe,Yozo Fujino. Dynamic characterization of multiple tuned mass dampers and some design formulas[J]. Earthquake Engineering and Structural Dynamics, 1994, 23(8): 813—835.