浮筏隔振系统的非共振响应分析

张树桢, 陈 前

(南京航空航天大学机械结构力学及控制国家重点实验室, 江苏 南京 210016)

引 言

目前浮筏隔振系统广泛的应用于船舶动力设备的隔振设计，其使用的隔振器(钢丝绳、空气弹簧及橡胶等形式)均具有不同程度的非线性刚度。由于浮筏系统尺寸较大，从而产生影响结构动力学特性的柔性变形。因此需要在理论研究阶段，分析隔振器的非线性刚度以及筏架和基础的柔性变形对系统动力学特性的影响。由于平置板式浮筏的结构简洁、特征明显，多作为分析和应用的重点。

在浮筏隔振系统的建模方面，文献[1]等在线性隔振条件下，采用四端参数法、模态机械阻抗综合法等子结构建模理论，分析了刚性筏架和柔性基础情况下的动力学响应。文献[2]提出使用柔性多体动力学理论，基于能量的方法对浮筏整体进行建模，方法新颖。由于非线性刚度的引入，导致公式较线性条件下更为复杂。文献[3，4]将弹性基础等效为单自由度的质量-弹簧系统，该方法根据经验公式进行计算，有计算处理快的优点，但经验公式难以涵盖多种尺寸及隔振器布置不同的结构。孟飞将局部非线性条件嵌入到有限元软件得到的复杂结构模态信息中，从而建立起结构的导纳矩阵并进行数值计算分析，拓展了复杂非线性结构的建模途径[5]。

非线性系统的定量分析方法主要适用于求解低维非线性系统的近似解，即以单自由度系统为代表的二维状态空间以及其他三维状态空间系统，而实际中的大多数动力学问题具有维数高、非线性强等特点，所以当前对非线性系统的分析以数值方法为主[6]。

本文将对平置板式浮筏进行动力学特性分析。将筏架和基础板均处理为柔性板结构，并设定隔振器具有立方非线性的刚度项，根据多刚体理论及板结构的偏微分方程，通过子结构方法进行线性条件下的建模，并通过多体刚柔耦合仿真，验证理论建模的合理性。在此理论基础上，引入隔振器刚度的非线性项并建立方程，以对非线性浮筏隔振系统进行多尺度法定量和数值计算分析，探索浮筏隔振系统的动力学特性。

1 浮筏隔振系统的动力学建模

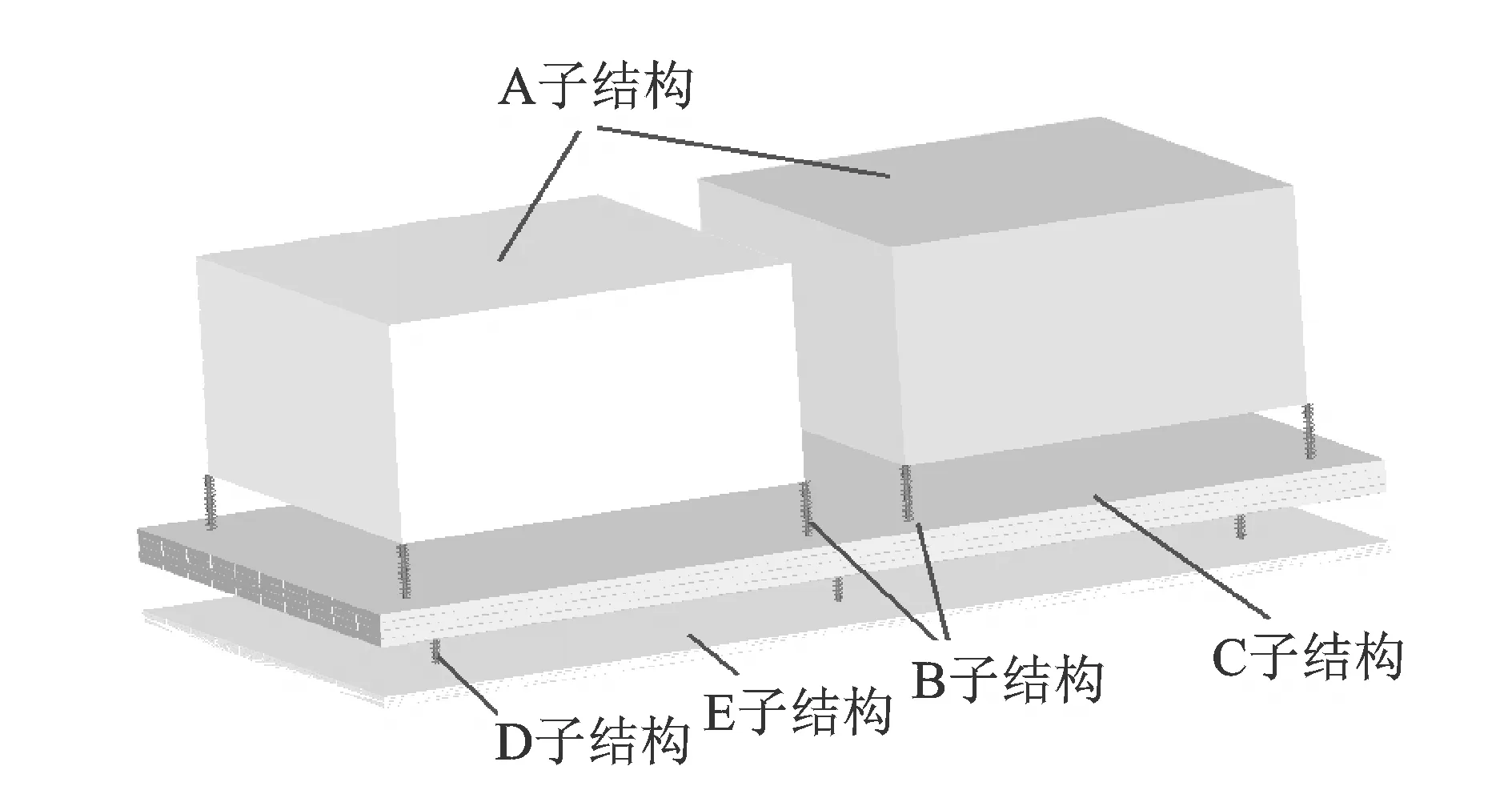
图1 浮筏隔振系统示意图

目前，单机组的双层隔振以及多机组的浮筏隔振系统(如图1)是舰船隔振效果较优且较常用的隔振手段。由于结构空间较为复杂，所以一般采用子结构方法进行分析。将整个系统分为A：机组；B:上层隔振器；C：中间质量或筏架；D：下层隔振器；E：基础板5个子结构。

各子结构间的力和位移边界条件如图2所示，其中的力及位移符号等均为6个方向的相关定义，如图2中的FAe所表示的激励力向量。通过考虑实际结构的工作条件，设A子结构为刚性体，C，E子结构为柔性体。

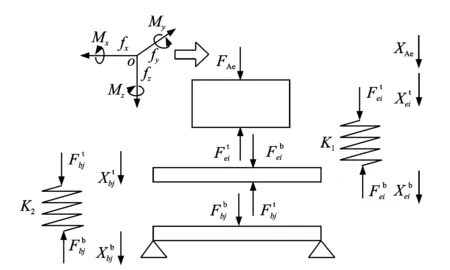
图2 浮筏隔振系统力和位移条件

A系统的动力学方程为

(1)

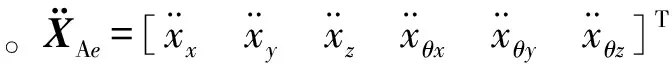
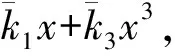
对B子结构分析，其作用力的表达式为

(2)

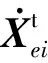
(3)

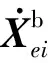
(4)

隔振器6个方向的刚度和阻尼表达式为：

其非线性刚度项为U。同理可以得到D子结构的作用力表达式

(7)

其各变量表达式和式(3)，(4)，(5)，(6)基本一致，V为对应的D子结构的非线性刚度项。不同的是其表示下层第j个隔振器。

对C和E子结构进行分析。柔性板结构弹性曲面微分方程的一般表达式为[9]

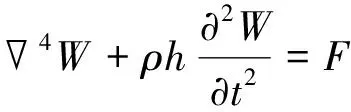
(8)

式中D*为板结构的复抗弯刚度，W为板的挠度，ρ和h分别为板结构的密度、厚度，F为板表面任意位置处受到的作用力。

取挠度的模态叠加表达式为

(9)

式中Wn(x,y)为板的振型函数，Cn为相应的模态坐标。

将式(9)的第n项代入式(8)，通过Galerkin方法处理得到板结构的常微分方程,由于涉及到积分变换，其符号表达式较为繁杂，所以将下文算例中的物理参数直接代入，考虑基础板结构的第1阶模态，得到表达式

(10)

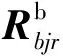
中间筏架的刚体运动，通过类似式(1)的分析得到

(11)

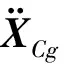
由上述分析，通过力和位移的边界条件，可以得到线性和非线性条件下的动力学方程组。线性方程的计算较快捷，而非线性计算由于算法的迭代，其耗时较长，且为探索非线性条件下的特性，将系统进行简化。在不考虑冲击等极限工况的前提下，隔振系统的实际工作环境较稳定，其轮机工作时所产生的激励一般为定频扰动，则可设机组的激励位置垂直于机组的重心，由于隔振器一般只在竖直方向存在非线性刚度，竖直方向的扰动不会引起各自由度间的耦合，所以只对竖直方向上的运动方程进行分析。通过多体动力学软件的时域分析以及理论模型的计算表明：对该隔振系统所具有的结构形式以及激励条件而言，柔性结构的一阶模态对系统的贡献量最大，所以只对一阶模态引入分析。由此将系统降为平面5个微分方程的方程组，分别为机组1和机组2的竖直运动、刚性筏架的竖直运动、柔性筏架的柔性变形以及基础板的柔性变形。设定弹簧原长为初始位置，由式(1)，(2)，(7)，(10)和(11)进行整理得到系统在竖直方向的运动微分表达式。其中刚性筏架柔性基础条件下的非线性浮筏的微分方程组如下

(12)

式中mz1和mz2分别代表两台机组的负载质量，其位移分别表示为x1和x2。作用于机组的力FAe分别表示为F1和F2，其大小相等。上层和下层隔振器的刚度项分别为k1和U以及k2和V，阻尼项分别为c1和c2。筏架的质量为mzc。表达式中的大写字母R均代表模态变换矩阵。

为保证理论的可信性，需对方程组式(12)及未列出的其他方程组进行正确性验证。由于非线性系统的仿真方法不够全面以及非线性试验条件的欠缺，难以直接对非线性方程的正确性进行验证。实际上，对隔振器刚度的非线性项进行删减，即可以得到线性条件下的动力学方程组，因此合理的线性模型，可以保证非线性模型的合理性。在本文中，图3为刚柔耦合软件仿真分析和线性理论计算结果的对比，并得到了较好的一致性，从而保证了该建模方法的正确性。另外，有限元软件的结果同样和刚柔耦合仿真分析结果基本吻合，保证了仿真的可靠性，同时刚柔耦合仿真方法的计算速度较优。

将式(12)用矩阵的形式表达为

(13)

以式(13)为例进行多尺度法的定量分析，将算例中的几何尺寸参数引入，同时将xcg表示为x3，xer表示为x4，整理得到各矩阵表达式如下所示

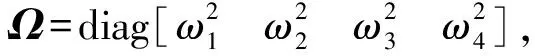
(14)

其中

由于式(14)的耦合程度较式(13)低，则分析较为快捷。设定c1=c2=ει，U=ευ，V=εν。引入两个时间尺度进行计算，设解为

yn=yn0(T0，T1)+εyn1(T0，T1)，n=1,2,3,4

(15)

取ε的零阶项，进行处理得到

(16)

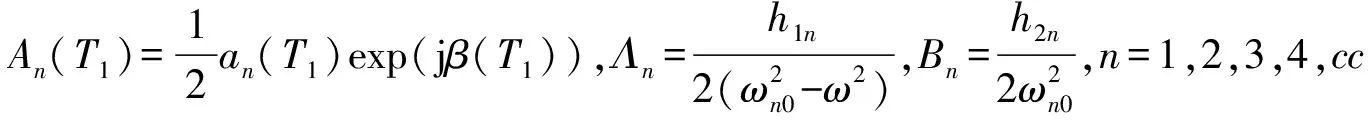
式中Nn为积分常数。βn的表达式，由于篇幅关系，在此不予展开。

强迫振动成分为

(17b)

初始偏移成分为

(17c)

由式(17)得到系统的解为：yn=ynz+ynq+ynp，n=1，2，3，4，再由X=ΦY，可以得到原系统的响应。由于阻尼的存在，自由振动完全衰减后，可以认为An=0，n=1，2，3，4，因此一阶近似解存在与激励力频率相同的强迫振动成分，且不受非线性项影响。刚度的非线性项对结构的影响主要体现在近似解中出现了复杂的共振项。分析得到系统的共振条件分为内共振和外激励引起的共振，以所在的项整理化简为例，将共振项可简单罗列为：ω4-ω1=-εO(1),ω2-3ω1=-εO(1)，ω2-2ω4-ω1=-εO(1)，ω2-ω4+ω3-ω1=-εO(1)等和2ω2-ω-ω1=-εO(1)，ω2-ω+ω3-ω1=-εO(1)等。可见共振条件极多，分析其内共振和主共振条件难以涵盖全面。考虑到实际系统并不处于共振区工作，所以本文主要通过数值计算，分析系统的非共振响应。

2 浮筏隔振系统的算例分析

目前，舰船中的动力机组以柴油机组为主，在正常状态下其转速分布在800～1 800 r/min，即15～30 Hz，所以重点分析较低频率段的结构动力学响应问题。建立如图1所示的刚柔耦合仿真的浮筏隔振系统虚拟样机模型，考虑到结构重心的调配，设定A子结构为2台相同的机组，且相对筏架对称布置；B子结构为机组和筏架间的隔振器，分2组，各4支隔振器；C子结构为板式筏架；D子结构为筏架和基础板间的隔振器组，共6支隔振器；E子结构为基础板。

具体物理参数为：负载机组1和机组2几何尺寸为0.8 m×0.8 m×0.4 m，密度为7 800 kg/m3。上下层隔振器根据负载质量，采用某型号的橡胶隔振器，竖直方向的刚度线性项为1×107N/m，非线性项U=V=1×109N/m3，阻尼比0.01。平置板式筏架的几何尺寸为2 m×1 m×0.06 m，结构损耗因子为0.01，自由边界。基础甲板的几何尺寸为2 m×1 m×0.02 m，结构损耗因子为0.01，简支边界。激励条件为作用于机组质心，竖直向下的简谐激励。对浮筏隔振系统，进行线性条件下的理论计算和多体动力学刚柔耦合仿真分析，以及非线性条件下的Runge-Kutta数值计算。

2.1 线性条件下的动力学特性分析

线性条件下的浮筏隔振系统引入筏架的前3阶和基础的前4阶模态，得到25个微分方程并进行分析。图3为无阻尼条件下的理论计算和多体动力学软件仿真的速度传递函数曲线。图4为理论计算的功率流曲线。

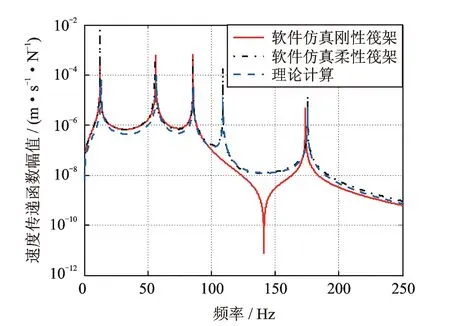
图3 浮筏隔振系统传递函数曲线图

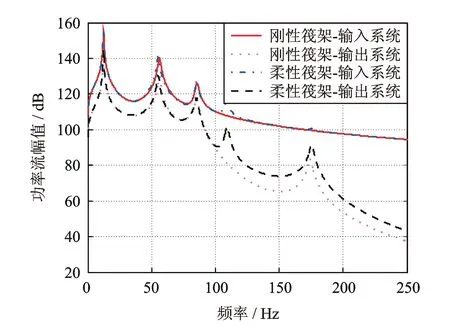
图4 浮筏刚性及柔性筏架功率流曲线

图3表明，在柔性筏架条件下，其峰值点从左至右依次为机组A子结构的上下运动共振频率点，筏架C子结构的上下运动共振频率点，基础E子结构的第1阶模态频率点，筏架C子结构的第1阶模态频率点，基础E子结构的第3阶模态频率点。由于激励条件对称，所激发的模态频率点均对应于对称模态。由多体刚柔耦合仿真解和理论解的一致性，验证了理论建模的可靠性，可以保证非线性分析结果的可信性，同时也佐证了该刚柔耦合建模方法的可行性。由图4所示，当将筏架考虑为柔性体，其功率流曲线较刚性筏架更加丰富，体现了筏架柔性的影响。除了筏架共振点外，刚性和柔性筏架条件下，输入到系统的能量基本一致。中高频段，柔性筏架所输出的能量较高，显然不利于隔振。实际条件下，筏架的跨度较大，必然要产生柔性变形，因此在结构设计阶段尽可能增大筏架的刚度，以降低不利影响。图3和4同时表明，刚性和柔性筏架在低频段的特性较为一致。

2.2 非线性条件下的动力学特性分析

分析立方非线性条件下的浮筏隔振系统，其结果如图5～8所示。

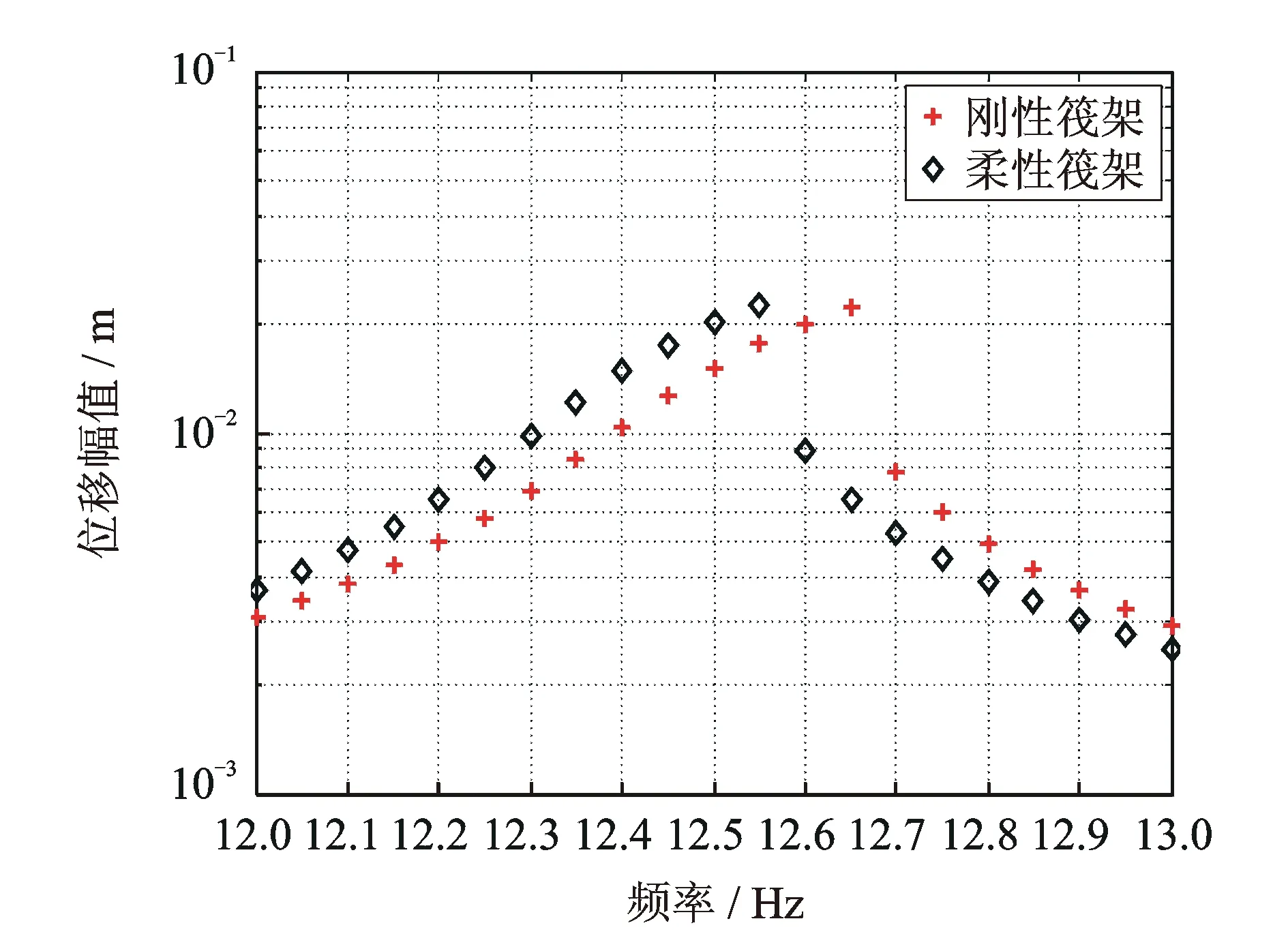
图5 机组1的主共振响应曲线

图6 非线性浮筏刚性及柔性筏架频谱图

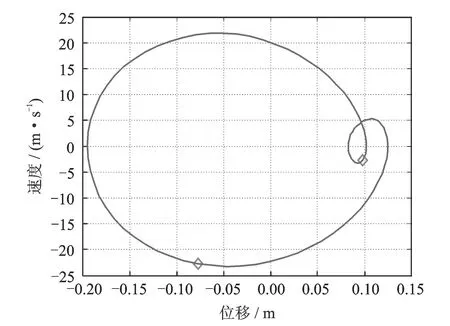
图7 机组1在大激励幅值下的相图

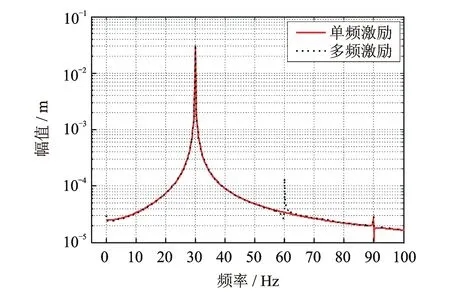
图8 单频及多频条件下的频谱图

对图5的分析表明，系统存在跳跃现象，曲线向右侧倾斜，证明了刚度渐硬参数的正确性。同时该图表明了柔性筏架隔振系统的一阶共振频率点较刚性筏架低，原因在于各子结构可等效为弹簧的串联，柔性结构的引入导致整体的刚度降低。图6为非线性条件下，单频简谐激励所产生的谐波分量，由于立方非线性项的存在，导致发生3倍于激励频率的谐波分量。其存在2倍于激励频率的谐波成分原因在于机组和筏架的质量作为常数项出现在方程组(13)中，导致分析时系统处于非对称刚度的状态，从而发生偶数倍的谐波成分，该非对称性，同样导致零频段存在较大的峰值。调整系统静平衡位置处的隔振器作用力对称于变形量，从而消除了方程组(13)中的质量常数项，修改后的结果如图8中的单频激励曲线所示，其只产生了奇数倍于激励频率的谐波。在实际工作环境中，隔振器的刚度在初始条件下难以对称于变形量，所以只存在立方非线性刚度的隔振器，也极有可能产生偶数倍的谐波分量。图5和6表明，非线性浮筏隔振系统，其刚性和柔性筏架条件下的动力学特性区别较为明显，这显著的不同于线性条件下的系统。

相同的激励及初始条件下，柔性筏架和柔性基础的系统可能发生图6及7中所示的倍周期运动现象，从而导致隔振设计难度更大，设计中需要对可能存在的激励频率进行全面的频谱特性分析。

动力设备在额定转速条件下也存在多个谐波分量的扰动，在浮筏系统的分析中，需要对该谐波激励条件进行分析计算。设定系统静平衡位置处的隔振器力-变形曲线对称于变形量，计算结果如图8所示，其不仅验证了前文中单频激励及对称刚度只产生奇数倍的谐波分量的结论，而且多频激励在60 Hz处的峰值也证明了谐波激励条件分析的重要性。

3 结 论

本文对柔性浮筏系统进行了动力学特性方面的研究。讨论了筏架的柔性变形以及非线性隔振器对系统的影响。主要结论为：

1)当激励幅值较小或非线性项较弱时,浮筏隔振系统处于线性工作条件。在动力学特性方面，柔性筏架系统相比于刚性筏架的区别主要体现在中、高频段。借助于多体动力学软件的刚柔耦合仿真分析，不但可以检验简单结构的理论建模的正确性，重要的是可以进行复杂结构的虚拟样机仿真分析，达到降低试验成本，缩短设计时间的良好效果。

2)非线性浮筏隔振系统的动力学特性较线性条件更为复杂。在线性理论正确性的基础上，引入隔振器刚度的立方非线性项，进行理论建模。通过考虑实际的工作条件，并以数值分析作为评价标准，使系统得以简化。而后通过数值方法分析了该隔振系统在单频和多频条件下的非共振响应。在相同的激励条件下，柔性筏架系统呈现出较刚性筏架更为复杂的动力学特性，在频谱上主要表现为更为多样的谐波成分，应在隔振设计时详细分析谐波分量诱发共振的条件。同时数值计算切实地表明了在非线性条件下的所有频段内，筏架的特性对系统的动力学特性影响显著，而不仅仅局限于线性系统的中、高频段。

参考文献：

[1] 刘保国.复杂隔振系统振动传递特性及实验研究[D].济南：山东大学，2007.Liu Baoguo. Research on power flow transmission and experiment of complex vibration isolation system[D] . Jinan: Shandong University, 2007.

[2] 俞翔，何其伟，朱石坚，等.柔性板基础隔振系统的柔性多体动力学理论建模[J].噪声与振动控制，2010,6:58—62.Yu Xiang, He Qiwei, Zhu Shijian, et al. Modeling of vibration isolation system with flexible plates based on the theory of flexible multi-body dynamics[J]. Noise and Vibration Control， 2010,6：58—62.

[3] Yu X, Zhu S J, Liu S. Study on performance of nonlinear vibration isolation under chaotic state[A]． Proceedings of the International Symposium on Safety Science and Technology[C]. Shanghai, China, 2004,4:1 417—1 421.

[4] 金卫军，黄其柏，廖道训.具有弹性地基的多层隔振系统的动力学方程[J].华中理工大学报,1999,27(6):48—50.Jin Weijun, Huang Qibai, Liao Daoxun. The dynamic equations of multi-layer vibration isolation system with elastic foundation[J]. Journal of Huazhong University of Science and Technology， 1999,27(6):48—50.

[5] Wei F, Zheng G T. Nonlinear vibration analysis of spacecraft with local nonlinearity[J]. Mechanical Systems and Signal Processing， 2010,24:481—490.

[6] 胡海岩.应用非线性动力学[M].北京：航空工业出版社，2000.

[7] 朱石坚，楼京俊，何其伟，等.振动理论与隔振技术[M].北京：国防工业出版社，2008.

[8] Goyder H G D, White R G. Vibration power flow from machine into built-up structures， Part l : Introduction and approximate analysis of beam and plate like foundation[J]. Journal of Sound and Vibration, 1980,65(l):59—75.

[9] 徐芝纶.弹性力学[M].第3版．北京：高等教育出版社，1990.