游梁式抽油机皮带纵向振动特性的仿真模型
邢明明, 董世民
(燕山大学机械工程学院,河北 秦皇岛 066004)
引 言
游梁式抽油机皮带传动系统具有如下特点:负载扭矩波动大、双向交变;电动机转速存在波动,特别是超高转差电动机驱动的游梁式抽油系统,电动机转速波动率可达到20%以上。负载扭矩以及电动机转速的大范围波动导致皮带纵向振动加剧,增大了皮带的摩擦功率损失,降低了皮带传动效率[1]。
皮带传动在大、中、小型机械中都有着广泛的应用。皮带在运转过程中,由于受离心力、带轮转速波动及负载扭矩波动等的综合影响,导致皮带弹性体存在振动。皮带传动系统的特性决定了皮带弹性体的振动受到带轮惯性质量的影响。皮带的振动不仅降低了皮带的传动精度和使用寿命,而且降低了带的传动效率[2~7]。为此关于皮带振动的研究引起了国内外学者的广泛关注,并提出了大量的有关带振动问题的模型[8~18]。文献[8~10]建立了带横向振动以及带的纵向振动模型,给出了带的滑移率与带振动的固有频率,分析了各结构参数对滑移因子的影响。文献[11~15]建立了带的动力学模型,提出了带振动及滑移率的测试方法,并分析了预紧力、阻尼等参数对带振动的影响。对于皮带纵向振动的研究文献[9,16]广泛采用以两个带轮转角为广义坐标的两自由度扭转振动力学模型,该模型将皮带简化为无质量的弹簧,两个带轮简化为两个具有转动惯量的圆盘;文献[14,17,18]将皮带简化为质量分布均匀的弹性体,建立了皮带纵向振动的数学模型,但没有考虑带轮转动惯量对皮带纵向振动的影响。鉴于目前皮带纵向振动模型的不足以及皮带纵向振动对游梁式抽油系统动力特性具有显著影响,本文进一步研究了游梁式抽油机皮带纵向振动特性仿真的力学与数学模型。该分析方法对以带传动为基础的机械系统动态特性的设计具有参考价值。
1 皮带纵向振动的力学模型
图1(a)为皮带传动装置示意图。

图1 皮带传动系统力学模型
S1为小带轮包角所对应圆弧的长度(m);S2为大带轮包角所对应圆弧的长度(m);R1为小带轮半径(m);R2为大带轮半径(m);Lt为皮带切线段长度(m);L为皮带节线长度(m);Je1为简化到小带轮处的等效转动惯量(kg·m2);Je2为简化到大带轮处的等效转动惯量(kg·m2);me1为简化到皮带上切点A1的等效质量(kg);me2为简化到皮带上切点C1的等效质量(kg);E为皮带材料弹性摸量(Pa);ρ为皮带材料密度(kg/m3);Med为简化到小皮带轮处的等效驱动力矩(N·m);Mbf为简化到大皮带轮处的等效阻力矩,即负载扭矩(N·m);Fed为简化到小皮带轮处的等效驱动力(N);Fef为简化到大皮带轮处的等效阻力(N)。
其中等效转动惯量和等效质量之间的关系,等效力矩与等效力之间的关系如下:
(1)
(2)
2 皮带纵向振动的数学仿真模型
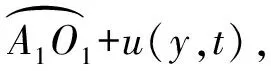
(3)
其中
(4)
式中a为声音在皮带中的传播速度(m/s);ω1为小带轮的角速度(rad/s);f(y,t)为皮带截面y在时刻t所受的分布激振力(N);ρ为皮带线密度(kg/m);A为皮带横截面面积(m2);u*为皮带基础运动(m/s);Sx为任意时刻t皮带截面X在运动曲线坐标系中的几何位置(m)。
由图1(b)所示的静止坐标系可见,分布力f(y,t)只在等效质点处作用有集中力Fed、Fef,其它截面分布力为零。根据动坐标与静坐标的变换关系,分布激励力f(y,t)为
(5)
Sx为任意时刻t皮带截面X′在静坐标系中的几何位置。由于皮带沿节线做周期性循环运动,而坐标x的取值范围为0≤x≤L,故Sx由下式计算
(6)
集中力Fed取决于小皮带轮处的等效驱动力矩Med;Fef取决于大皮带轮处的等效阻力矩Mef。限于篇幅,等效驱动力矩Med、等效阻力矩Mef的计算方法见文献[1],本文不再赘述。鉴于本文重点是研究皮带的纵向振动特性,同时根据实际油井等效驱动力矩Med与等效阻力矩Mef的变化规律,将Med和Mef简化为[18]
(7)
式中M0,M1和M2为系数;ω为大皮带轮转动的平均角速度(rad/s)。ω与抽油机悬点冲程次数n之间的关系为
(8)
式中iBox减速箱传动比。
游梁式抽油机工作时,曲柄轴净扭矩周期性波动,即电动机负载扭矩周期性波动,从而导致电动机转速周期性波动,即小皮带轮转速周期性波动。由公式(3)可见,小皮带轮角速度波动是皮带纵向振动的激励,相当于振动理论中基础运动所导致的系统受迫振动。小皮带轮角速度可以展开为傅式级数,为便于讨论小皮带轮角速度波动对皮带纵向振动特性的影响,将小皮带轮角速度简化为
ω1=ω0+K0cos(ωt)
(9)
式中ω0为小带轮平均角速度(rad/s);K0为小皮带轮角速度波动幅值(rad/s)。
3 自由振动的固有频率与振型函数
系统自由振动方程为
(10)
系统自由振动的通解
u(x,t)=U(x)sin(ωnt+φ)
(11)
式中ωn为系统自由振动的固有频率(rad/s);φ为任意常数,由系统初始条件决定。
振型函数U(x)为
(12)
式中b=ωn/a;B1,B2,D1和D2为由边界条件决定的待定系数。
皮带纵向振动在两个质点me1和me2处满足连续性条件
(13)
将式(11)和(12)代入上式可得固有频率方程
A1A2-A3+A4=0
(14)
式中 参数A1,A2,A3和A4由下式计算
(15)
式中 参数C1,C2和C3和C4表示为
(16)
方程(14)是关于未知数b的超越代数方程,应用数值法可求得前n个根b1,b2,…,bn以及皮带纵向振动的前n阶固有频率为ωni=abi(i=1,2,…,n)。与ωni对应的第i阶振型函数为:
(17)
式中 系数λ1i,λ2i和λ3i为
(18)
式中 系数ψ1i,ψ2i,ψ3i和ψ4i的表达式为
(19)
式中E1i,E2i,E3i和E4i的表达式为
(20)
4 受迫振动的稳态响应
根据主振型对质量的正交性,可得正则振型函数
(21)
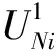
(22)
式中
(23)
式中 参数QNi表达式为
(24)
正则激振力为
pi(t)=Fed(t)UNi(x)|x=0-Fef(t)·UNi(x)|x=L1-
(25)
正则坐标下的运动微分方程
(26)
通过运用振型叠加原理,将皮带弹性体的纵向振动偏微分方程(3)简化为式(26)所示的n个相互独立的无阻尼单自由度系统的受迫振动微分方程。应用四阶龙格库塔法并采用零初始条件分别求正则坐标qi(i=1,2,…,n)的稳态响应。
系统受迫振动的动态响应
(27)
要得到运动坐标下系统受迫振动的动态响应,需通过变换公式。UNi(x)与UNi(y)变换关系如下:
当0≤Sx (28) 当L1≤Sx (29) 系统在运动坐标系下受迫振动的动态响应 (30) 式中UNi(y)为阵型函数;qi(t)为模态坐标。 以下仿真计算的基本参数为:传动带长度L=4 m;带切线段长度Lt=0.97 m;单根皮带线密度ρ=0.37 kg/m;皮带根数z=4;单根皮带横截面积A=1.55×10-4m2;摩擦系数μ=0.6;小带轮半径R1=0.15 m;大带轮半径R2=0.45 m;皮带弹性模量E=2×108Pa;冲次n=6 min-1;减速箱传动比iBox=35;减速箱传动效率ηBox=95%;大皮带轮平均角速度ω=21.99 rad/s。 当ω0=65.97 rad/s,k0=150 rad/s;M0=1 200 N·m;M1=0;M2=0;时,图2和3给出了皮带传动系统对转速波动的动态响应曲线。 图2 皮带某点纵向振动的瞬时位移随时间变化曲线 图3 皮带某点瞬时速度随时间变化曲线 当M0=-400 N·m;M1=400 N·m;M2=1 500 N·m;ω0=65.97 rad/s,k0=0时,图4~5给出了皮带传动系统对载荷激励的稳态响应曲线。 图4 皮带某点纵向振动的瞬时位移随时间变化曲线 图5 皮带某点的瞬时速度随时间变化曲线 由图2~5可得以下结论: (1) 系统转速波动加剧了皮带的纵向振动,影响了皮带的瞬时位移与瞬时速度,皮带的瞬时位移和速度出现剧烈波动; (2) 与系统转速波动激励的响应相比,外载荷波动激励对皮带纵向振动产生较大的影响,皮带的瞬时位移与瞬时速度不仅出现剧烈波动而且振幅较大。 图6 带轮振动的瞬时位移随时间变化曲线 图7 带轮瞬时转速随时间变化曲线 图8 主从动带轮的转差随时间变化曲线 当M0=-400 N·m;M1=400 N·m;M2=1 500 N·m;ω0=65.97 rad/s,k0=150 rad/s时,图6和7给出了大小带轮瞬时位移与瞬转速随时间变化曲线,图8给出了传动系统大小带轮的转差随时间变化曲线由以上图可知: (1) 考虑带轮的惯性质量对皮带纵向振动的影响,带轮的瞬时位移呈周期性波动,小带轮的瞬时振动位移明显大于大带轮的瞬时振动位移; (2) 带轮的瞬时转速呈周期性波动,小带轮的瞬时速度高于大带轮转化到小带轮处的瞬时等效转速,说明大小带轮之间存在瞬时转差; (3) 受皮带纵向振动的影响,大小带轮瞬时转差呈现简谐波动;当瞬时转差为负值时,小带轮被拖动;瞬时转差的存在说明皮带传动系统瞬时传动比不恒定,皮带与带轮之间存在滑差。 (1) 考虑带轮惯性质量对皮带纵向振动的影响建立了两坐标系弹性体纵向振动的力学与数学模型。应用坐标变化法求解系统受迫振动的响应,仿真分析了转速波动以及负载扭矩的波动对皮带纵向振动的影响。该分析方法对带轮附件驱动系统的动态特性的设计具有理论与实际意义; (2) 转速波动激励与载荷波动激励使得皮带纵向振动的瞬时位移与瞬时速度出现周期波动;其振动幅值受到带轮惯性质量的影响; (3) 带轮瞬时振动位移受其惯性质量的影响,惯性质量越小瞬时振动位移越大;带轮瞬时转差的存在说明皮带瞬时传动比不恒定,皮带与带轮之间存在相对滑动。 参考文献: [1] 董世民.抽油机井动态参数计算机仿真与系统优化[M].北京:石油工业出版社, 2003.Dong Shimin.Couputer Simulation of Dynamic Parameters of Rod Pumping System and System Optimization[M]. Beijing: Petroleum Industry Press,2003. [2] Musselman M, Djurdjanovic D. Tension monitoring in a belt-driven automated material handling system[J]. CIRP Journal of Manufacturing Science and Technology, 2012,(5): 67—76. [3] Tan Feng Lee, An ChyauHuang. Vibration suppressioninbelt-drivenservosystemscontaininguncertain nonlineardynamics[J]. Journal of Soundand Vibration, 2011,(330): 17—26. [4] Shirong Zhang, Xiaohua Xia. Optimal control of operation efficiency of belt conveyor systems[J]. Applied Energy, 2010, (87): 1 929—1 937. [5] Jean-Philippe Gauthier, Philippe Micheau. A model based on experimental data for high speed steel belt CVT[J]. Mechanism and Machine Theory, 2010, (45): 1 733—1 744. [6] Zhang ShaoJun, Wan Zhong, Liu GuangLian. Global optimization design method for maximizing the capacityof V-belt drive[J]. Science China Technological Sciences,2011:140—147. [7] Shirong Zhang, Xiaohua Xia. Modeling and energy efficiency optimization of belt conveyors[J]. Applied Energy, 2011,(88): 3 061—3 071. [8] Igor V. Andrianov, Wim T. van Horssen. On the transversal vibrations of a conveyor belt:Applicability of simplified models[J]. Journal of Sound and Vibration,2008,(313):822—829. [9] 罗善明, 余以道, 郭迎福,等.带传动理论与新型带传动[M]. 北京:国防工业出版社, 2006: 62—78.Luo Shanming, Yu Yidao, Guo Yingfu,et al. Theory of Belt Driving and New Belt Driving [M]. Beijing: National Defence Industry Press, 2006:62—78. [10] 王小莉, 上官文斌, 花正明. 单根多楔带传动系统带横向振动的计算方法[J]. 振动工程学报,2010, 23(6):604—615.Wang Xiaoli, Shangguan Wenbin, Hua Zhengming. A method for calculating belt transverse vibration in serpentine belt drive systems[J]. Journal of Vibration Engineering, 2010, 23(6): 604—615. [11] Ulsoy Ag, Whitesel Je, Hooven Md. Design of belt-tensioner systems for dynamic stability[J]. Journal of Vibration Acoustics Stress and Reliability in Design,1985,107:282—290. [12] 王红云, 上官文斌, 张少飞. 阻尼多楔带传动系统建模及带滑移控制分析[J]. 振动、测试与诊断, 2011, 31(1): 59—63.Wang Hongyun, Shangguan Wenbin, Zhang Shaofei. Model construction of serpentine belt drive systems with multi-ribbed belt damping and belt slipping control [J]. Journal of Vibration, Measurement & Diagnosis, 2011, 31(1): 59—63. [13] 上官文斌, 张智, 许秋海. 多楔带传动系统轮—带振动的实测与计算方法研究[J]. 机械工程学报, 2011, 47(21): 28—36.Shangguan Wenbin, Zhang Zhi, Xu Qiuhai. Experiment and calculation method for pulley-belt vibrations in serpentine belt drive system[J]. Journal of Mechanical Engineering, 2011, 47(21): 28—36. [14] Hou Youfu, Meng Qingrui. Dynamic characteristics of conveyor belts[J].Journal of China University Mining & Technology, 2008, (18): 629—633. [15] Gregor epon, Lionel Manin, Miha Boltezar. Introductionofdampingintotheflexiblemultibodybelt-drivemodel: Anumerical and experimental investigation[J]. Journal of Soundand Vibration, 2009, (324): 283—296. [16] 邢明明, 董世民, 崔阳, 等. 游梁式抽油机皮带传动效率的仿真模型[J]. 工程力学, 2013,30(7): 242—247.Xing Mingming, Dong Shimin, Cui Yang, etal. Simulation model of transmission efficiency of the belt-driving systems of beam pumping units[J]. Engineering Mechanics, 2013, 30(7): 242—247. [17] Dong Shimin, Xing Mingming. Simulating sliding efficiency of belt driving acted on by bi-directional alternating load [A]. Advanced Materials Research[C]. 2011, 308-310: 1 900—1 909. [18] 邢明明, 董世民. 游梁式抽油机井皮带滑动效率的仿真研究[J]. 中国机械工程,2013,24(2):245—251.Xing Mingming, Dong Shimin. Simulation of sliding efficiency for belt driving in beam pumping unit[J].China Mechanical Engineering, 2013, 24(2):245—251. [19] Pravin M, Singru, Jayant P, Modak. Dynamics of arm of a flat belt drive pulley with explanationof belt flutter[J]. Journal of Sound and Vibration, 2005 (279): 1 037—1 070.5 仿真实例与结果分析
5.1 系统对转速波动的响应
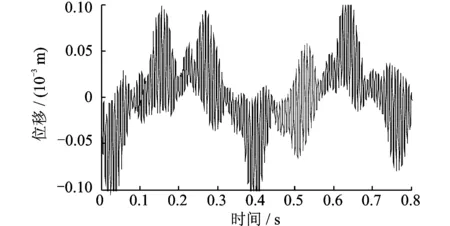
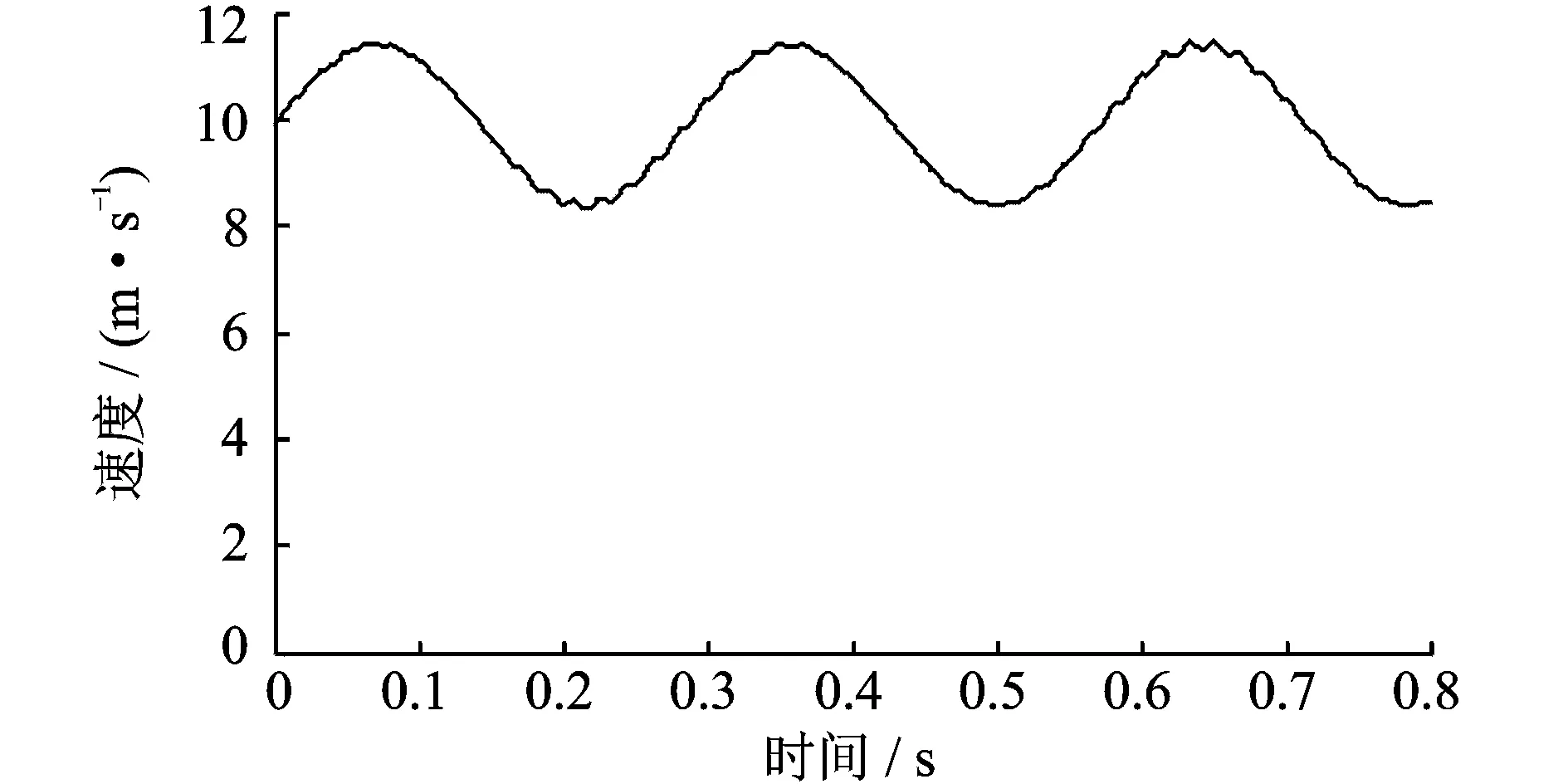
5.2 系统对载荷激励的响应
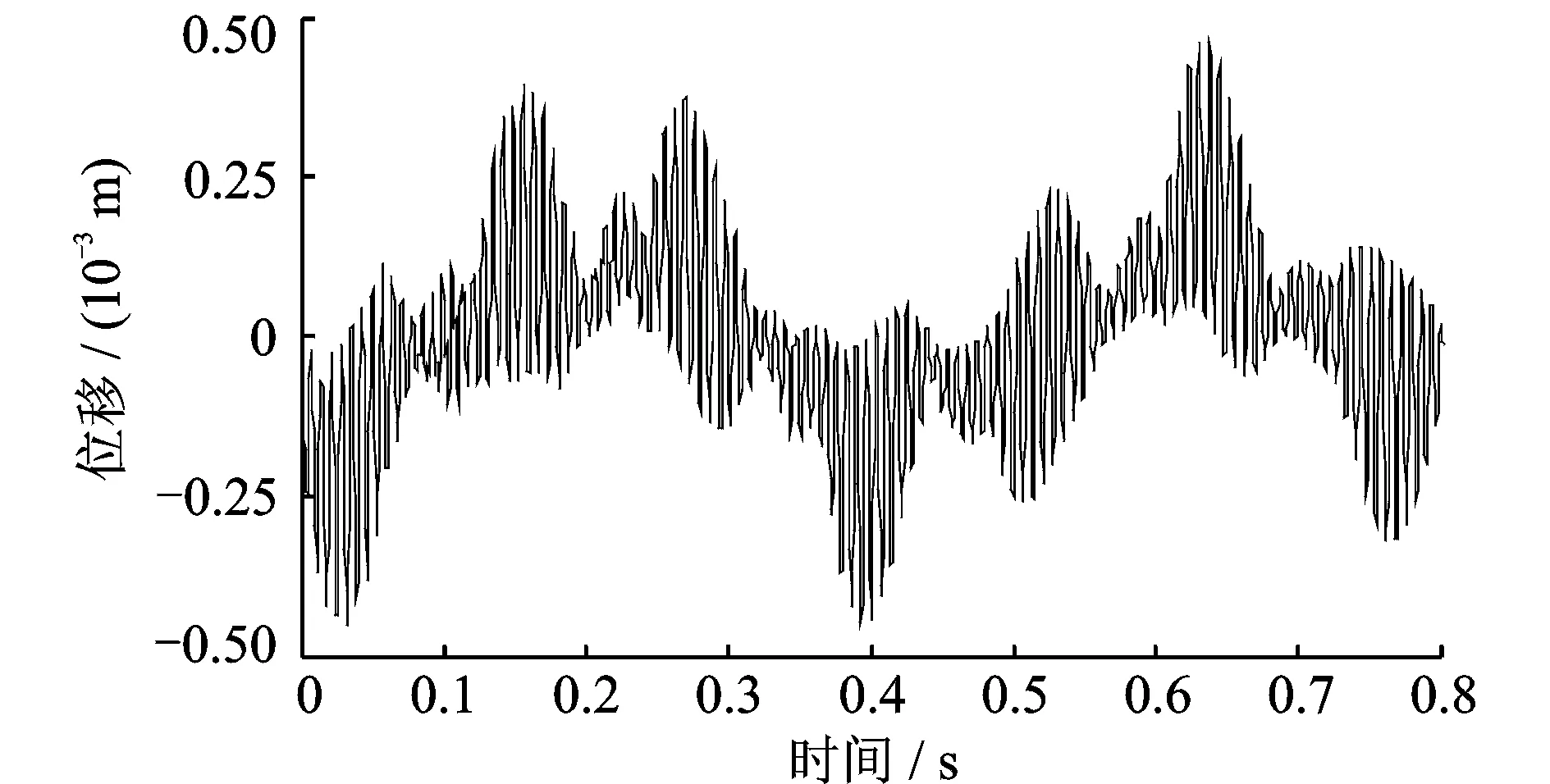
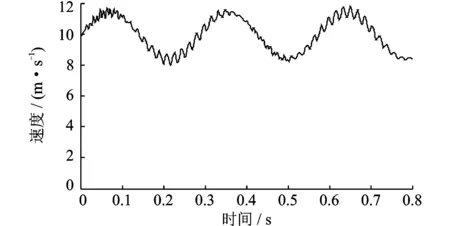
5.3 系统对转速与载荷激励的响应

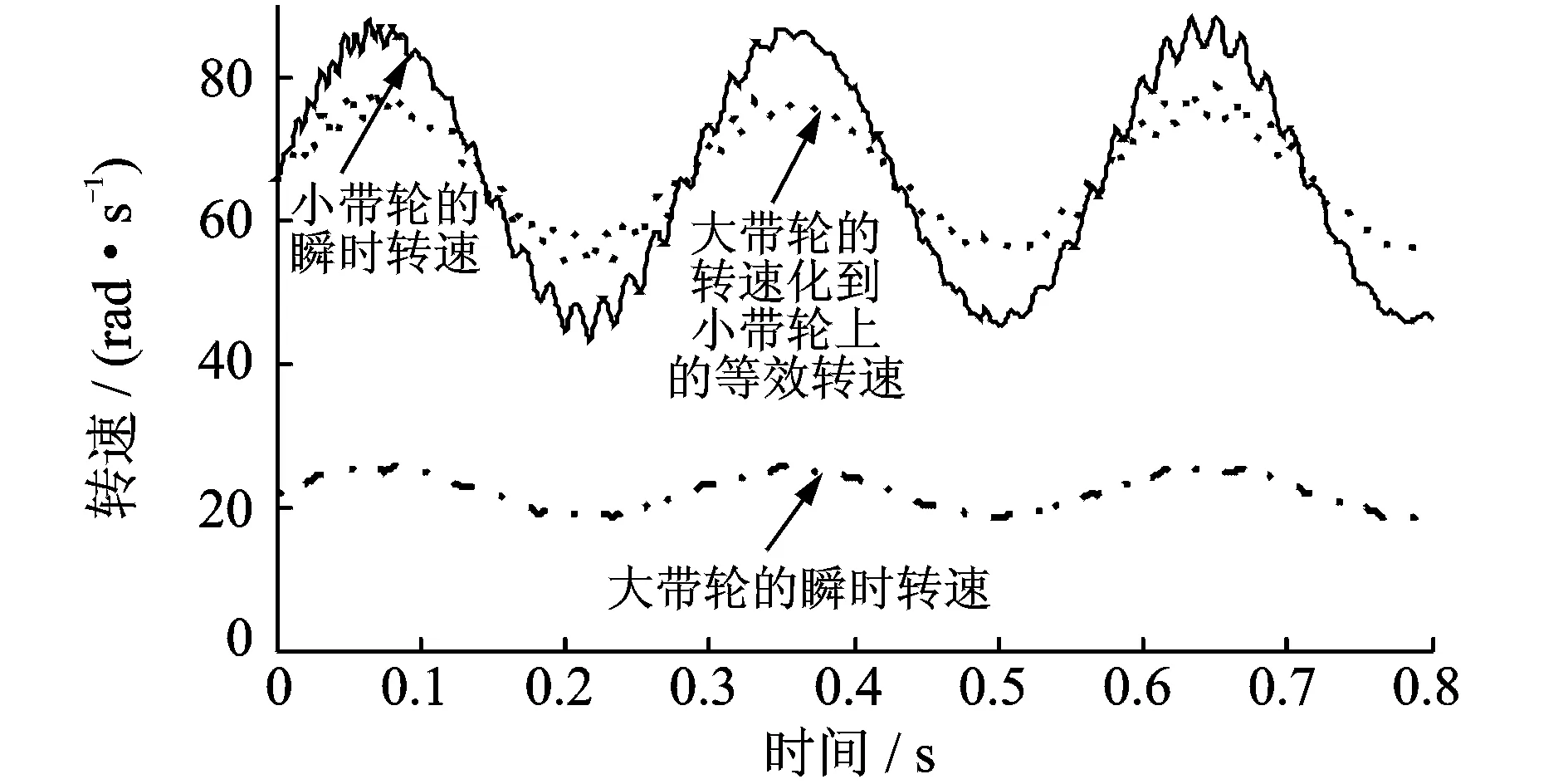
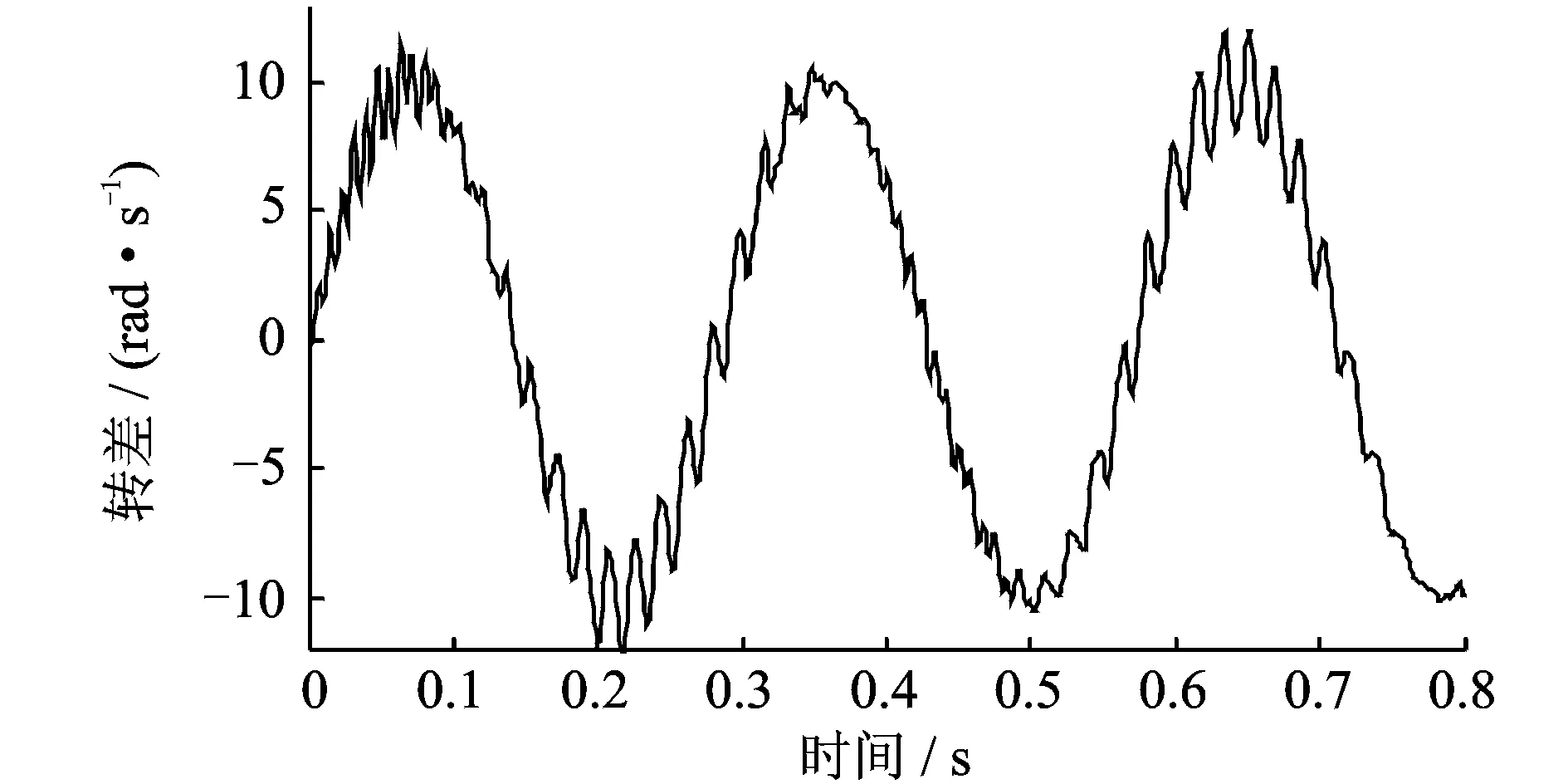
6 结 论

