初始攻角对钻地弹斜侵彻土壤影响的数值模拟
周玉兵,郭锐,周昊,张鹏
(1.南京理工大学 机械工程学院,江苏 南京 210094;2.73862 部队,江西 上饶 334111)
0 前言
钻地弹又称侵彻弹,是一种能够钻入目标深层并引爆的弹药,是针对重要目标实施“外科手术”的重要武器,其对土壤的侵彻问题是军工领域、防护工程领域一个重要的研究课题。
斜侵彻是弹体攻击目标常见的一种运动状态,是最典型的碰撞问题。此过程涉及高温、高压、高速,以及结构内的部分材料的破坏,是冲击动力学研究的难点问题之一。
本文运用ANSYS/LS-DYNA 软件,研究在弹体速度为1 000 m/s,30°斜侵彻土壤时,通过改变初始攻角大小(取初始攻角为5°,8°,12°),建立侵彻模型,进行数值模拟,总结出初始攻角对钻地弹斜侵彻土壤运动轨迹和规律的影响。
1 建立模型
采用ANSYS 前处理程序建立模型。基本单位取为cm-g-μs,弹体及靶板均采用SOLID164 实体单元。土壤靶体均匀,由于斜侵彻土壤靶板为对称问题,为减少有限元单元划分数量,节约求解时间,利用无反射边界条件建立二分之一模型进行计算。弹体与土壤靶板网格单元均采用Lagrange 算法,用三维实体单元划分网格,在对称面上施加对称边界约束,靶板边界施加固定约束。弹体长度为300 mm,直径为60 mm,内腔壁厚10 mm,壁深200 mm,密度ρ=7.83 ×103 kg/m3,头部形状为卵形(30°,半径为180 mm 两条圆弧相交组成而成),斜侵彻土壤靶板,土壤靶板尺寸为5 000 mm ×3 000 mm ×90 mm。弹体模型如图1 所示。

图1 弹体模型图
由于计算机求解等条件的限制,取土壤宽度(x向)为5 000 mm,高度(y 向)为3 000 mm,厚度(z 向)为90 mm,且弹体与土壤之间的夹角为30°。侵彻模型如图2。

图2 弹体斜侵彻土壤模型
网格划分如图3。

图3 弹体斜侵彻土壤模型网格划分
2 材料模型参数建立及修改k 文件
本文计算材料模型参数单位制采用cm-g-μs 制。弹体为刚性,所有节点自由度都耦合到刚体质量中心上,材料参数的选择要符合真实性,即材料杨氏模量、泊松比、剪切模量和密度等材料参数要符合实际情况。钻地弹弹体和土壤模型的材料参数如表1 和表2 所示。

表1 弹体模型主要参数

表2 土壤模型主要参数
用UltraEdit 软件程序打开K 文件,将材料模型修改为上述的材料参数,具体如下:


计算结束后,运行LS- PROPOST 程序查看计算结果,得到弹体的轨迹图、速度加速度等时程曲线,最后进行结果分析。
3 数值模拟及分析
为总结出初始攻角对斜侵彻土壤的运动轨迹和规律的影响,本文取弹体侵彻速度1 000 m/s,弹体侵角30°,三个初始攻角分别为5°,8°,12°通过数值模拟,从各自在土中的运动轨迹、侵彻深度、速度和加速度曲线的比较中得出影响规律。
侵彻轨迹如图4-图6 所示。

图4 初始攻角为5°时弹体侵彻轨迹图

图5 初始攻角为8°时弹体侵彻轨迹图

图6 初始攻角为12°时弹体侵彻轨迹图
由钻地弹在土中的运动轨迹图可以看出,弹体侵入土壤后,土壤质点被弹体排开。土壤的排开主要靠弹头部完成,因此土壤阻力也主要作用在弹头部上。弹体在土壤中的弹道为曲线,说明弹体在侵彻过程中发生了偏航。通过比较,三条弹道都存在不同程度的弯曲,其中初始攻角为12°弹体的侵彻轨迹弯曲程度最大,表明弹体在侵彻过程中弹道偏航角度最大。弹体初始攻角越大侵彻弹道偏转越大,弹体初始攻角越小侵彻弹道偏转越小。
从图7 来看,不同初始攻角时弹体侵彻土壤x 轴方向的深度差别不是很大。但从图8 弹体斜侵彻土壤的y 轴深度比较图来看,弹体侵彻土壤的深度差别比较明显,初始攻角为12°时弹体侵彻深度最小,初始攻角为5°时弹体侵彻深度最大。从而得出,弹体侵彻土壤时初始攻角越小,侵彻的深度越大,弹体的侵彻深度随初始攻角的减小而增大,也就是说,攻角越小,弹体的侵彻深度越大,当攻角为0°时,弹体的侵彻深度可达到最大。因此,在使用钻地弹打击深层地下目标时,尽量使攻角减小,以便获得较大的侵彻深度。
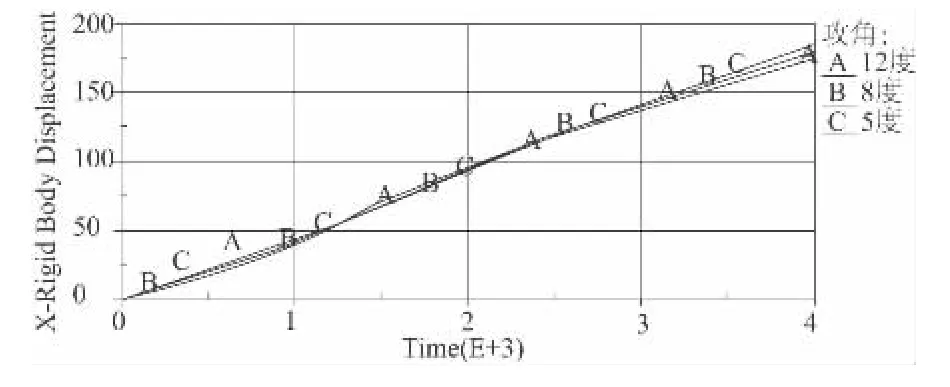
图7 不同攻角的弹体斜侵彻土壤的x 轴深度比较图
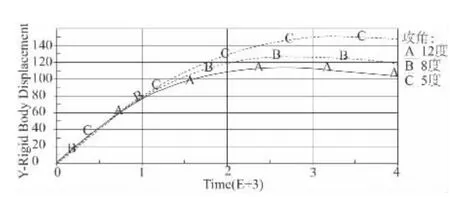
图8 不同攻角的弹体斜侵彻土壤的y 轴深度比较图
初始攻角对弹体斜侵彻土壤的运动规律有很大影响,从速度时程比较图9 可以看出,初始攻角为5°的弹体速度减小相对比较慢,而攻角为12°时弹体速度减少相对比较快。从加速度时程比较图10 来看,弹体攻角为12°时,斜侵彻土壤的加速度在500 μs 左右的时候获得最大值,明显比初始攻角为5°和8°的弹体大,初始攻角为8°的弹体在1 000 μs 时获得最大值,其值比初始攻角5°的大,初始攻角5°的加速度最大值最小。在弹体带攻角斜侵彻时,其入射角等于攻角和弹体侵角之和。所以,攻角越大相当于入射角越大,如初始攻角为5°时,相当于弹体的入初始攻角为12°时,相当于弹体的入射角为射角为35°,42°,也就是说,当弹体初始攻角变大时,使得入射角变大。弹头与土壤碰击过程中,入射角大的弹体侵彻土壤时与土壤接触面积大,所受土壤阻力也就越大,因此其加速度也就越大。由于弹体入射方向与弹体运动方向不一致,在继续侵彻过程中,初始攻角大的弹体受到的不对称阻力大于攻角小弹体,从而使得偏航角度逐渐加大,并且随着攻角的增大,弹体轨迹弯曲弧度越大,即弹体在土壤中的弹道越弯曲。
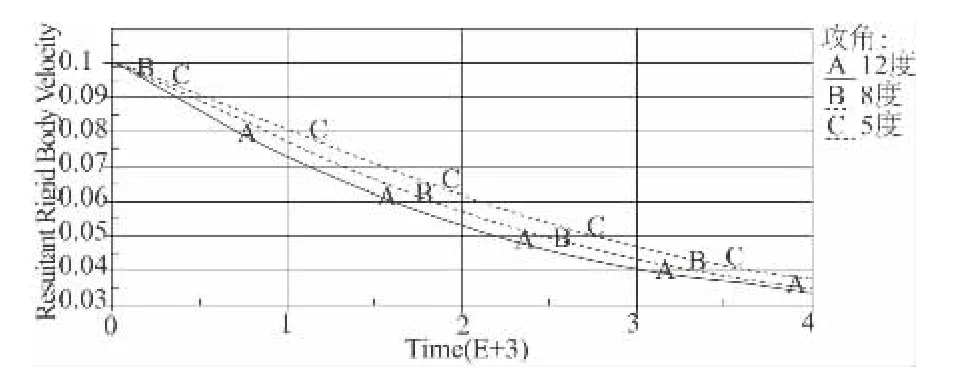
图9 不同初始攻角的弹体斜侵彻土壤的速度时程比较图
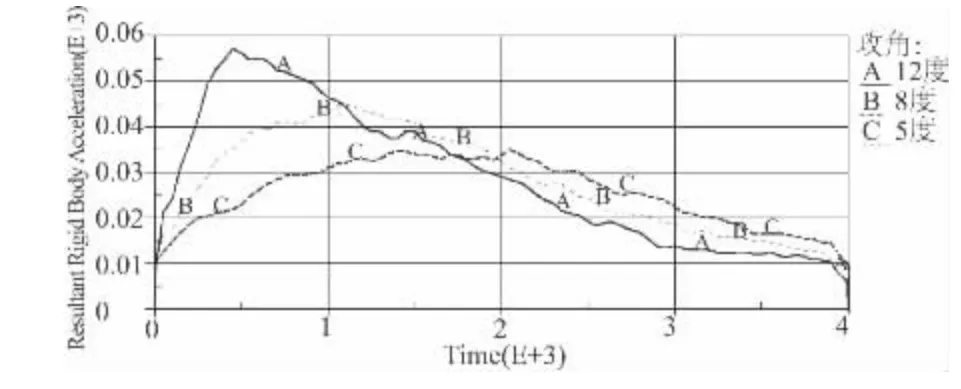
图10 不同初始攻角的弹体斜侵彻土壤的加速度时程比较图
4 结论
本文应用ANSYS/LS-DYNA 软件,对钻地弹侵彻土壤的过程进行了数值仿真,研究结果表明:
1)斜侵彻土壤时,弹体运动轨迹都出现了一定程度的弯曲。
2)弹体侵彻土壤时,初始攻角越小弹体偏航越小,侵彻深度越大。
3)初始攻角对钻地弹斜侵彻土壤有很大影响。同一速度下,初始攻角增大时,弹头受到的阻力变大,减加速度变大,弹体速度下降越快,弹体弹道弯曲弧度增大。初始攻角减小时,弹头受到的阻力变小,减加速度变小,弹体速度下降越慢,弹体弹道弯曲弧度减小。
[1]穆军.美军实施“外科手术”的关键武器——钻地弹[J].现代兵器,1999,5.
[2]张建斌.基于ANSYSILS-DYNA 的弹头侵彻问题分析与研究[D].西安:西安电子科技大学,2009.
[3]周燕.钻地弹土中弹道影响因素的数值模拟研究[D].南京:南京理工大学,2009.
[4]时党勇,李裕春,张胜民,等.基于ANSYS/DYNA8.1 进行显示动力分析[M].北京:清华大学出版社,2005.
[5]周培毅,李世才,等.钻地弹侵彻混凝土靶的数值分析[D].北京理工大学学报,2003,4(23):357-361.
[6]尹放林,王明洋,等.弹丸斜入射对侵彻深度的影响[J].爆炸与冲击,1998,18(1):69-76.

