液力偶合器额定工况流场数值计算

何延东

(辽宁石油化工大学机械工程学院,辽宁抚顺113001)

0 引言

液力偶合器内部流动为非常复杂的粘性、三维、非定常气液两相流动，本文借助CFD软件平台对调速型液力偶合器额定工况下不同充液率的流场进行数值计算，得到偶合器内部速度与压力分布，以及不同充液率下流场结构的变化及两相分布情况，揭示其流场的流动规律和特性。

1 控制方程

偶合器内部为湍流流动，故应用连续方程、时均化雷诺方程和k-ε湍流模型，则有:

式中:εm——涡粘性系数；

V——流体质点速度矢量；

F——单位质量力；

p——压力；

μ——动力粘度；

k——湍流能量；

ε——湍流能量耗散率；

cμ——系数，常取 0.09。

k和ε的运输方程为:

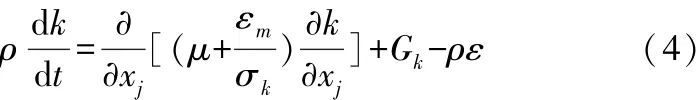
其中

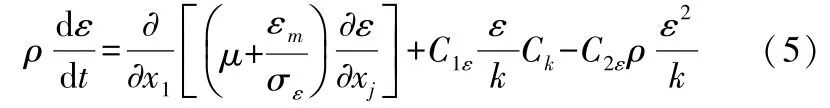
式中常数一般取:σk=1.0；C1ε=1.44；C2ε=1.92；σε=1.3。

流体在偶合器内作气液三维粘性两相流动的连续方程为:

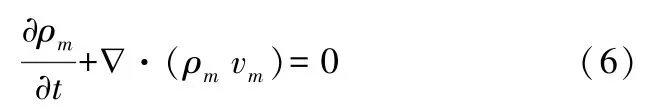
其中:

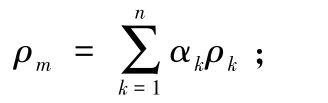
vm—质量平均速度；

ρm——混合密度；

αk——第k相的体积分数。

两相流动的动量方程可以通过对所有相各自的动量方程求和来获得。可表示为:

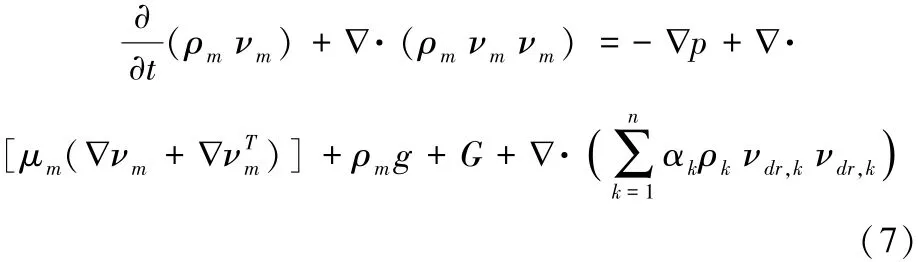
其中

n——相数；

G——体积力；

∇——哈密尔顿算子；

μm——混合粘性。

第二相p的体积分数方程为:

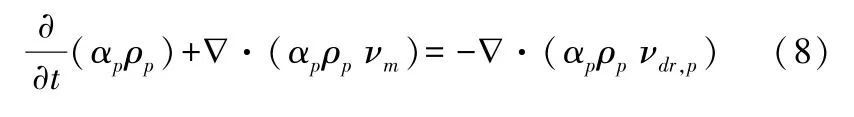
2 CFD建模

根据已有的偶合器有机玻璃模型进行三维建模，图1为CFD计算模型和网格模型。

图1 流道的计算模型和网格模型

液力偶合器的内部流动是非稳态的，而且泵轮流道与涡轮流道之间存在强烈的相互作用，为统一计算，对泵轮流道与涡轮流道的交界面采用滑动网格理论，将泵轮流道和涡轮流道统一计算。

滑动网格技术是一种非定常计算方法，它用到两个或多个网格区域，每个网格区域至少有一个边界的分界面，该分界面区域与另一网格区域相邻。相邻网格区域的分界面相互联系形成“网格分界面(Grid-interface)”，简称Interface(交界面)，如图2所示。计算过程中，单元区域沿着网格分界面相对滑动，而两个区域的网格不会发生变化。当泵轮转动时，泵轮与涡轮网格区域相对Interface产生滑移，交界面上信息按照滑移理论进行传递。

3 流场分析

3.1 整体流场分析

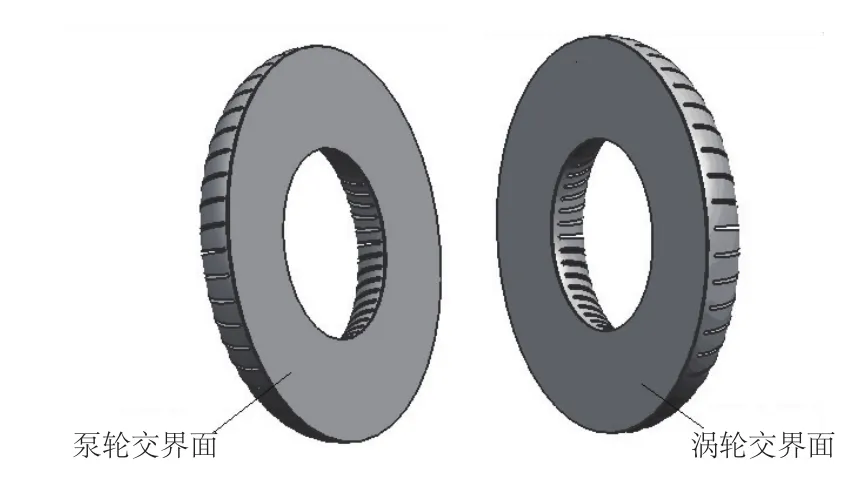
图2 滑动网格边界设置

3.1.1 整体流场压力分布

图3为不同充液率液力偶合器整体流场的压力分布图。额定工况下泵轮与涡轮的转速差很小，相应的循环流量也很小，因此泵轮与涡轮流道的压力分布非常具有规律性，沿径向成比例逐渐增加，在泵轮出口与涡轮入口处达到最大。同时流道内循环流量较小，速度的变化也较小，使得速度对压力变化的作用降低；粘性作用与偶合器的液力损失有关，额定工况下，能量损失很小，因此粘性作用对压力变化的作用也不大。综上所述，额定工况下后两者的作用逐渐降低，那么离心力的作用就越来越重要，因此压力的分布会呈现沿径向比例分布的趋势。在离心力的作用下，叶片的高压区出现在叶片上部与外环的交界区域。小充液率时的低压区高于大充液率，二者的高压区分布大小相近。额定工况下压力值比较小，而且压力分布比较均匀，充液率的不同对压力值有较大影响。

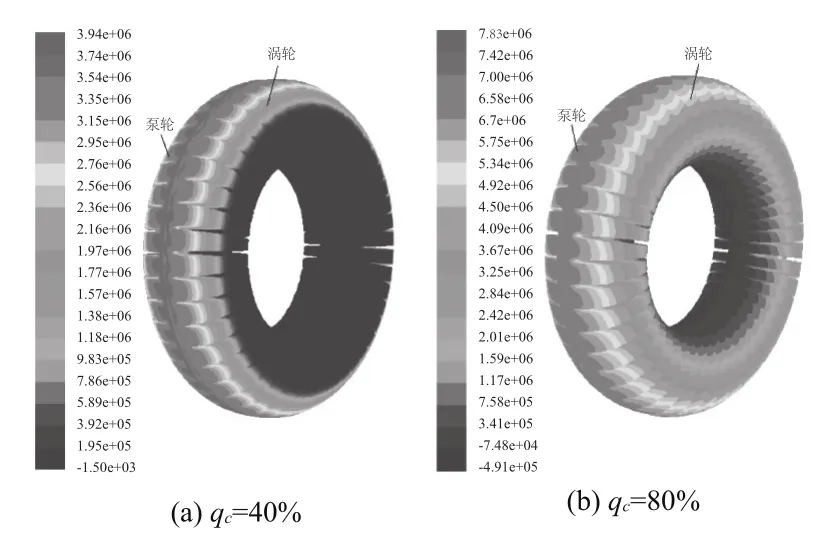
图3 整体流场压力分布图

3.1.2 整体流场速度分布

图4为不同充液率下的整体流道速度分布。由图4可以看到，此时液流为大循环流动。泵轮与涡轮的速度分布非常具有规律性，速度值沿径向成比例逐渐增加，流道中心处流速较低，泵轮出口与涡轮入口处为流道的高速区。与压力分布不同的是，两种充液率下的速度分布相近。对比不同充液率下偶合器的流场速度分布，可见充液率的不同对速度的大小没有较大影响。额定工况下泵轮与涡轮的速度相差不大，这样使得二者的流动较为顺畅，没有出现不规则流动现象。

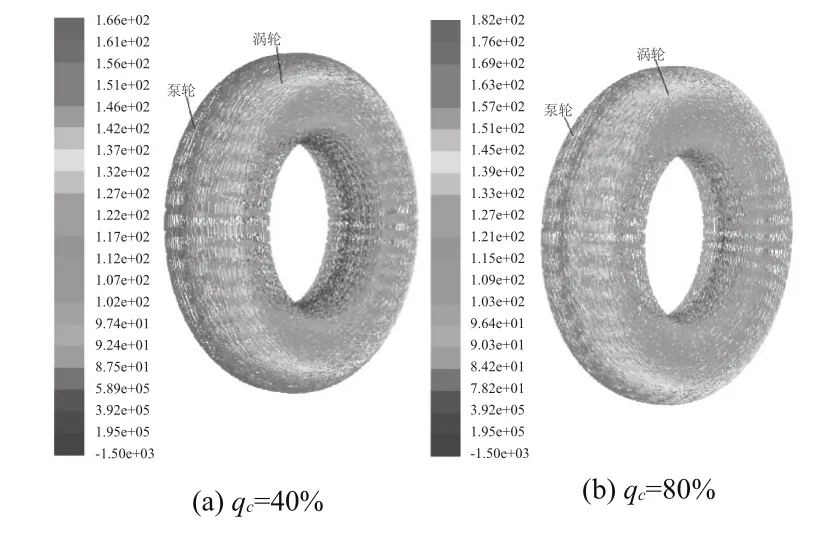
图4 整体流场速度分布图

3.1.3 液相体积分布

图5所示为液力偶合器在不同充液率下的液相体积分布。对比图5(a)、(b)可以发现，充液率为40%时，液体全部集中在偶合器的外环上部，流道的大部分空间被气相所占据，充液率为80%时，气体只集中在流道的中心区域。

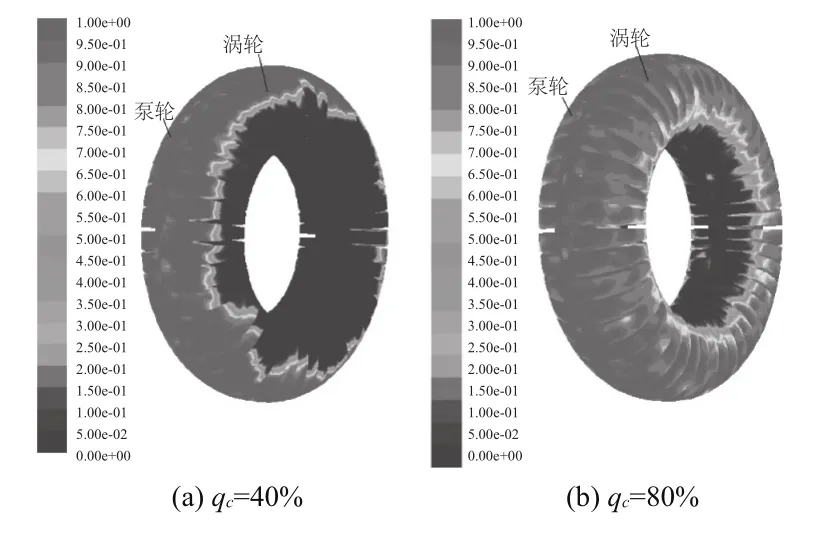
图5 液相体积分布图

3.2 轴面流场分析

3.2.1 叶片压力面流场分析

图6所示为不同充液率时泵轮与涡轮叶片压力面的压力分布情况。从图6中可以看出，叶片压力面的分布比较有规律，其值沿径向逐渐增大，在泵轮出口与涡轮入口处压力值达到最大。小充液率时的低压区远远高于大充液率时的低压区。大充液率的压力分布由叶片下部向上部非常规律的沿径向逐渐增加。对比图6(a)、(b)发现充液率的不同对压力大小有较大影响，充液率大的压力差较大。

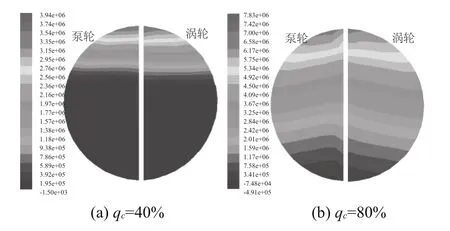
图6 压力面压力分布图

图7 为叶片压力面的速度矢量分布情况。可以看出，两种充液率下的速度分布相同，下部液流速度小于上部，整体速度分布都逐渐趋于沿径向成比例分布。泵轮与涡轮的速度分布比较平稳，没有二次流等不规则流动的出现。

图7 压力面速度分布图

3.2.2 叶片吸力面流场分析

图8与图9分别为额定工况下叶片吸力面压力和速度分布图。

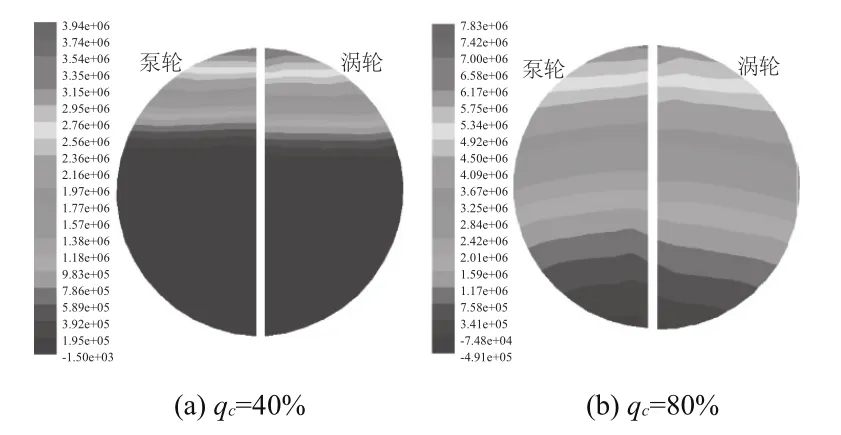
图8 吸力面压力分布图

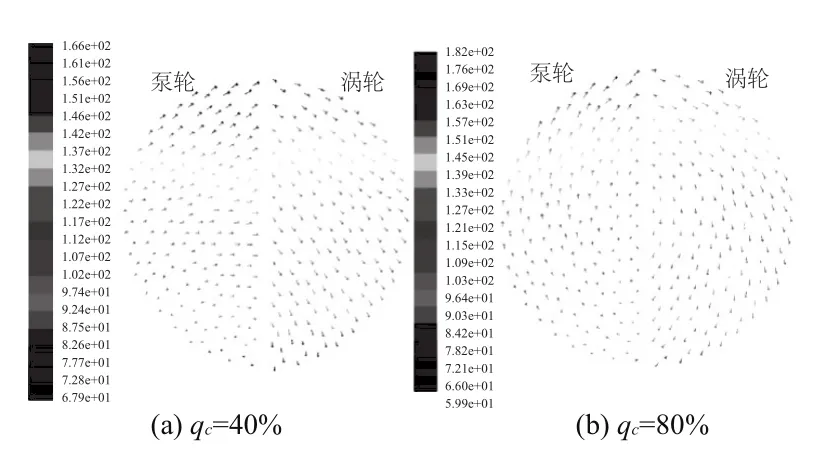
图9 吸力面速度分布图

从图中可以看出叶片吸力面的压力分布与速度分布和压力面的分布相同，泵轮与涡轮流道的压力与速度分布具有一定的规律性，压力值与速度值沿径向成比例逐渐增大，均在泵轮出口与涡轮入口处达到最大。

3.2.3 中间轴面流场分析

如图10所示，分别在泵轮与涡轮流道内的轴面内作剖面A-A、B-B，该剖面能够显示泵轮与涡轮中间轴面方向上的压力场与速度场。

图11与图12分别为额定工况下中间轴面的压力和速度矢量分布图。

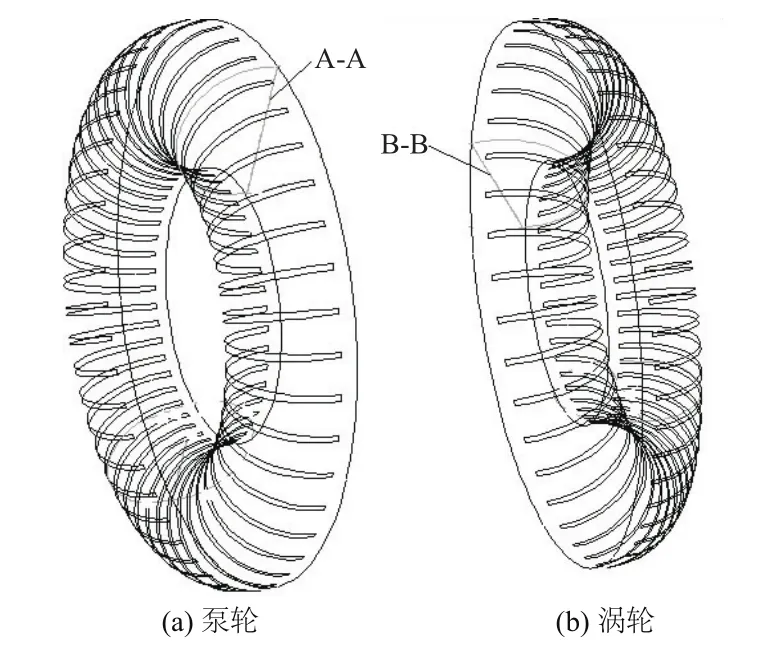
图10 中间轴面示意图

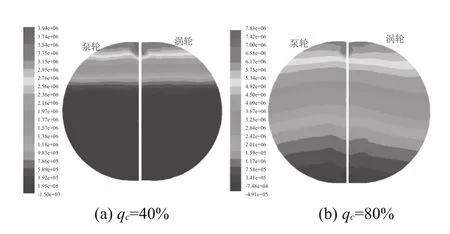
图11 中间轴面压力分布图

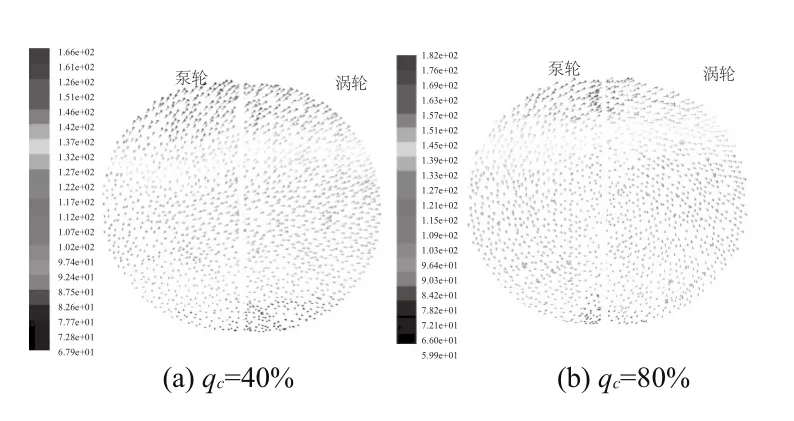
图12 中间轴面速度分布图

从图11中可以看出，额定工况下能量损失降低，粘性作用对压力变化的作用也降低，离心力的作用越来越重要，因此压力分布会呈现沿径向比例分布的趋势，且呈带状分布，在离心力的作用下叶片的高压区出现在叶片上部与Interface的交界区域。低充液率下中间轴面的低压区较大。

从图12中可以看出，不同充液率下的速度分布沿径向逐渐增加。由于额定工况下泵轮与涡轮速度转速差较小，可以看到中间轴面的速度方向为泵轮与涡轮的旋转方向，没有出现偏向涡轮的分速度。不同的是，低充液率下的高速区分布范围大于高充液率。

3.3 Interface流场分析

图13与图14分别为不同充液率Interface的压力和速度分布情况。

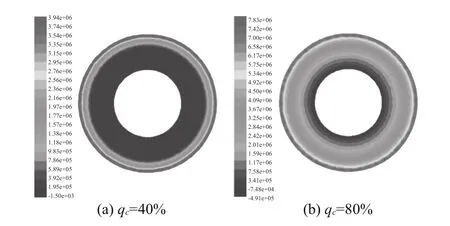
图13 Interface压力分布图

图14 Interface速度分布图

图13 中(a)、(b)对比可知，高压区出现在 Interface的外环，即泵轮出口与涡轮入口区域，低压区出现在内环，即涡轮出口与泵轮进口区域。不同的充液率对Interface的压力分布有较大影响，充液率小时低压区域明显多于大充液率区域，因此大充液率的总体压力值较大。

从图14中可以看出，不同充液率下Interface的速度分布完全相同，且沿径向逐渐增大，在Interface的内环速度最小，外环速度最大，即泵轮出口区域和涡轮入口区域的速度达到最大值。

4 结语

对调速型液力偶合器额定工况下不同充液率时叶轮叶片与整体流道的流场进行数值计算与分析，初步揭示了偶合器在额定工况两相流场的速度和压力分布情况，数值模拟的结果基本反映了流道内部流动的基本特征。CFD计算可以应用于液力偶合器的设计，从而改变传统设计方法需多次试制方可定型的弊端，在计算机上实现设计过程，达到准确、省时和省力的目的。

[1]万天虎，赵道利，梁武科，等.基于CAD/CFD分析系统的流体机械翼型优化[J].流体机械，2005，33(11):37-39.

[2]余志毅，曹树良，王国玉.叶片式混输泵内气液两相流的数值计算[J].工程热物理学报，2007，28(1):46-48.

[3]才委，马文星，刘春宝，等.基于三维流场计算的液力变矩器特性预测方法[J].哈尔滨工程大学学报，2007，28(3):316-319.

[4]项昌乐，肖荣，阎清东，等.牵引-制动型液力变矩器流场分析[J].工程机械，2005(5):43-46.

[5]何志霞，袁建平，李德桃，等.柴油机喷嘴喷孔内气液两相湍流场三维数值模拟[J].内燃机工程，2005(6):18-21.

[6]卢金铃，席光，祁大同.离心泵叶轮内气液两相三维流动数值研究[J].工程热物理学报，2003(2):237-240.

[7]李雪松，马文星，吴允柱.液力偶合器制动工况三维流场数值模拟及制动转矩计算[C].第四届全国流体传动及控制学术会议论文集.大连，2006:659-664.