基于大数据分析的段塞流持液率预测模型

郑 琳，刘 云

（长江大学石油工程学院，湖北武汉 430100）

管道中气体和液体的两相流在石油工业中经常发生，多相管流一直是石油工业中的一个重要问题[1]。持液率是指管道内实际的液体体积分数，通常是计算压力损失时最重要的参数，同时对预测水合物的形成和蜡的沉积也是必要的[2]。段塞流是气液两相流体管道中常见的流型之一，它对管道的腐蚀以及下游分离器的设计等都有很大的影响[3]，段塞流持液率是段塞流模拟的一个重要参数。对于持液率的预测，国内外的学者提出过不少机理模型和经验模型，大都是基于流型的预测，然后根据流型计算相对应的持液率[4]。目前来看，根据流型计算持液率是最准确的一种方式。

Ghassan 等[5，6]利用水平和倾斜管流共423 组实验数据提出了一种新的计算段塞流持液率的经验公式，该关系式是混合物速度、液体黏度和倾斜管倾角的函数。大倾角管道是极其容易出现段塞流的管路结构，但是此经验公式的管道倾角应用范围为-10°～9°，并不能用于大倾角的计算。Beggs 等[7]对水平和倾斜管道进行了实验研究，根据大量的实验数据得到相关关系，该模型可以用于不同流型下以及-90°～90°倾角的持液率计算[8]。经过分析，在上坡管段且对应的水平持液率大于0.309 7 时，并不能用此相关式计算持液率[9]。Eaton等[10]在不考虑流型，只考虑流体性质和流量的情况下，得到了水平管道下的无因次模型。对于倾斜管的段塞流持液率预测，依旧存在问题。结合现有预测模型存在的问题，本文将Eaton 的无因次模型和Beggs-Brill 的倾角校正系数结合的方法建立一个新的预测模型，利用大数据方式对各因素分析并划分，将划分范围后得到的洛-马参数和Y 参数与持液率的数据点进行多项式拟合，最终得到一个只用于预测段塞流持液率的新模型。

1 灰色关联度分析

Ros[11]在大量实验和理论工作的基础上，排除了持液率可以忽视的几个变量，证实影响持液率的六种主要因素为管径、气体表观速度、液体表观速度、液体黏度、液体密度和液体表面张力。在已有经验的基础上，利用灰色关联度分析的方法进一步确定各因素对持液率的影响程度。

灰色关联度是能反映两种指标之间相关程度的一种数学分析方法。简单来讲，把持液率作为参考序列，而影响持液率的指标就是比较序列，最后通过灰色关联度分析就可以得到各指标分别与持液率的相关程度，灰色关联度越大，说明它对持液率的影响力越大[12]。

灰色关联度的计算步骤如下：

设Xi={x（ik）│k=1，2，…，n }为比较序列，X0={x0（k）│k=1，2，…，n }为参考序列。

（1）数据无量纲化处理。

（2）求差序列。选取参考序列，假设各时刻xi与x0的绝对差值为Δ，则有：

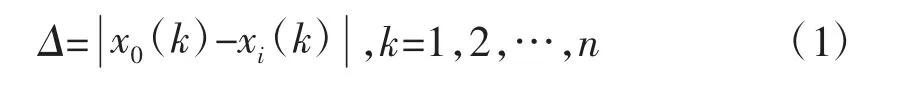
（3）求两极最小差与最大差。两极最小差Δmin=miniminkΔ，两极最大差Δmax=maximaxkΔ。

（4）计算灰色关联系数。求得第i 个比较序列第k个指标与参考序列第k 个最优指标值的关联系数，即ξi（k）为：

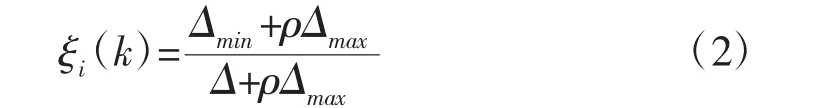
式中：ρ∈（0，1）-分辨系数，一般取ρ=0.5；ρ 值越小，分辨力越大，引入该系数是为了提高关联系数之间的差异显著性。

（5）计算灰色关联度。平均值法求得灰色关联度为：

2 模型构建

Gregory[13]利用已有的实验数据，运用7 种方法对倾斜管内气液两相流的持液率进行了预测验证，结果表明，在管道倾角大于10°的情况下，管道倾角对预测持液率的影响不大。于是，本文忽略小倾角对持液率的影响，减少不必要的倾斜校正，将0°～90°的倾角范围分为水平及微倾角0°＜θ≤10°和大倾角10°＜θ＜90°两个部分进行模型的构建，使得模型的精确度更高。

2.1 水平及微倾角

在预测持液率的所有模型中，Eaton 的无因次模型并不是根据流型划分，但是无因次准数使得数据的适应性好，在既考虑流型又考虑数据适用性的情况下，利用无因次模型专门对段塞流进行预测是可行的。

Eaton 等[10，14]提出的持液率相关公式为：

式中：HL-持液率；A-任意函数；Nlv-液体速度准数；Ngv-气体速度准数；Nd-管径准数；NP-归一化的压力；Nl-液体黏度准数；Nlb-基础黏度影响数，Nlb=0.002 26。

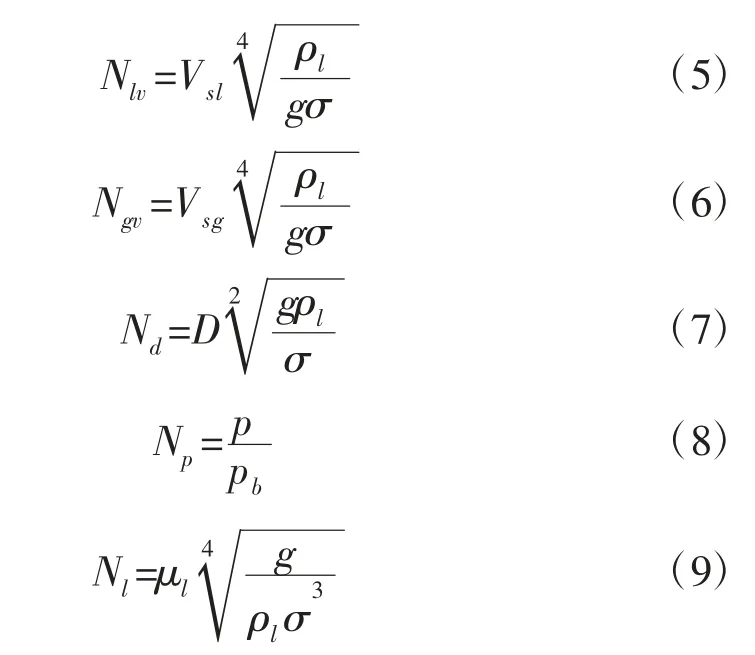
式（5）～（9）中：Vsl-液体表观速度，m/s；ρl-液体密度，kg/m3；σ-表面张力，N/m；Vsg-气体表观速度，m/s；D-管径，m；p-压力，Pa；pb-气相计量的基准压力，pb=14.65；μl-液体黏度，Pa·s。

Lockhart 等[15]曾将持液率数据与洛-马参数相关联，并绘制了相对应的曲线图，此结果说明洛-马参数与持液率之间存在着一定的函数关系。在此结论基础上，本文也利用洛-马参数进行水平及微倾角下段塞流持液率的分析。

洛-马参数为：

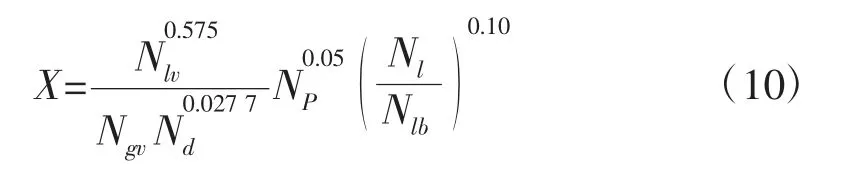
2.2 大倾角

对于两相流管道来说，管道倾角是影响持液率的一个重要因素，Beggs 等对倾斜管道下的持液率进行了实验研究，得到了倾斜校正系数与角度之间的关系，用于修正水平管道的两相流动。于是本文将Beggs-Brill的倾斜校正系数与Eaton 模型相结合，用于计算大倾角下的两相段塞流。

Beggs-Brill[7]提出的倾斜校正系数的公式如下：

式中：C-系数；θ-倾角。

上坡且流型为段塞流时，C 的求解公式如下：

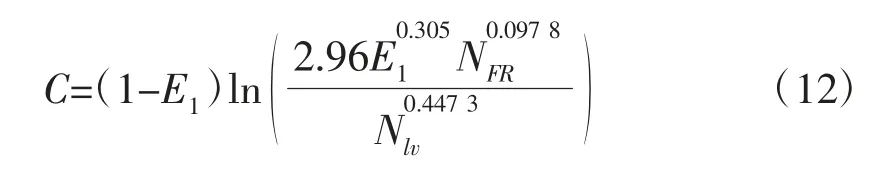
式中：E1-体积含液率，；NFR-弗劳德准数，；Nlv-液相速度准数。

根据在水平及微倾角下的洛-马参数的应用，引入新的参数Y，用于大倾角下段塞流持液率的分析。新参数Y 的计算公式为：

3 模型验证

为了建立段塞流持液率的预测模型，将取自众人研究的721 组数据用于开发预测新模型[17]，随机选出46 组数据用作测试新模型的准确性，剩余675 组数据用于建立模型。实验数据的来源以及一些流动参数的范围（见表1、表2）。

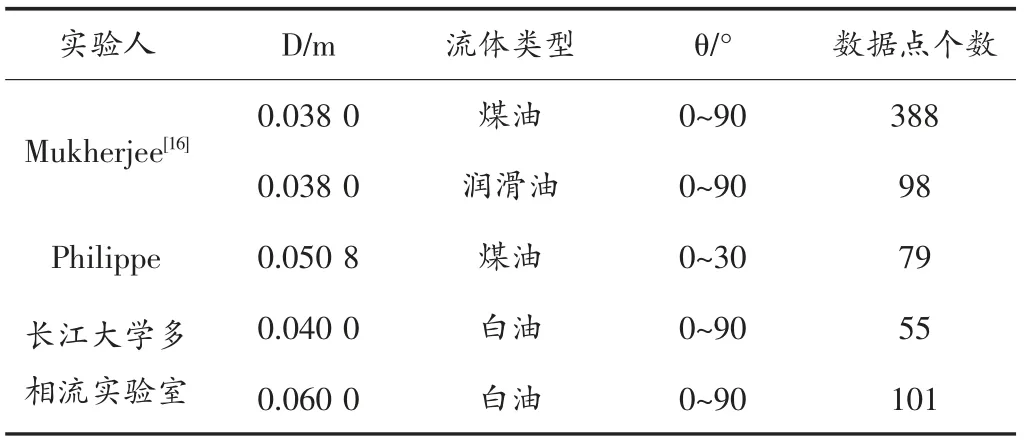
表1 数据的来源Tab.1 Source of data

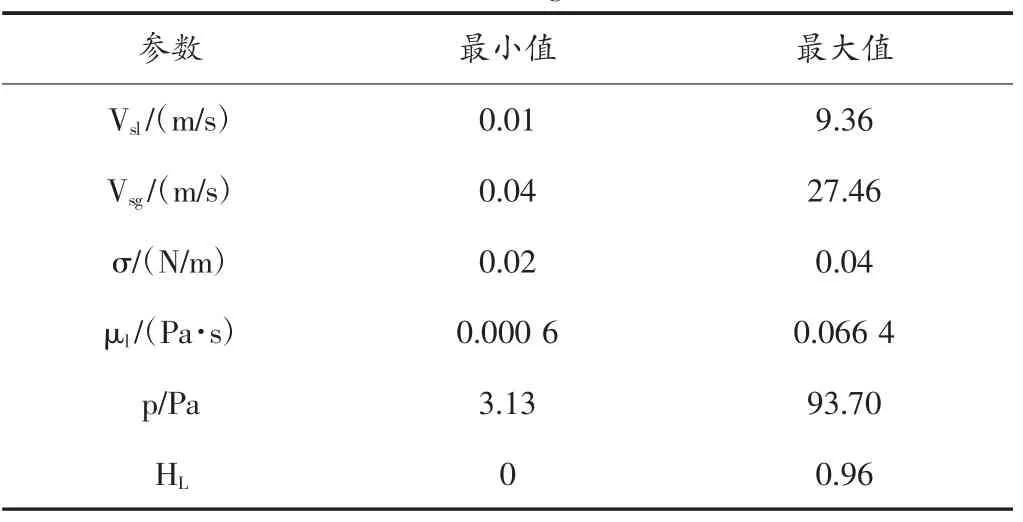
表2 数据的有效范围Tab.2 Valid range of data

实验室数据是借助长江大学多相流实验平台得到的，此平台可以开展在不同倾角、不同温度和压力下等多个条件下对油、气、水三相混合介质多相管流动态研究，实验流体为白油和空气，通过实验系统的动力系统、管路系统、控制系统、储存系统、数据采集系统等共同完成[18]。

3.1 数据分析

Eaton 模型在影响持液率的六项因素的基础上建立了无因次准数，还另外引入了压力的无量纲数，本文利用灰色关联度对这五项相关因素进一步分析。各项因素对持液率影响程度的结果（见表3）。

通过表3 可以看出，对持液率影响程度的排序为：管径准数>归一化的压力>液体速度准数>液体黏度准数>气体速度准数，本文将灰色关联度分析得到的前三种主要因素作为标准进行范围划分，建立不同范围下的持液率预测模型，使得整个段塞流持液率预测模型有范围针对性且更加精确。

表3 各项因素对持液率的影响程度Tab.3 The degree of influence of various factors on liquid holdup

3.2 验证结果

利用软件对洛-马参数和Y 参数与持液率的数据点进行多项式分析拟合后发现，实验数据点与曲线y=（p1x2+p2x+p3）/（x+q1）的相关性极大，多重判定系数均在0.95 以上，某一范围内数据点与曲线的对比图（见图1）。

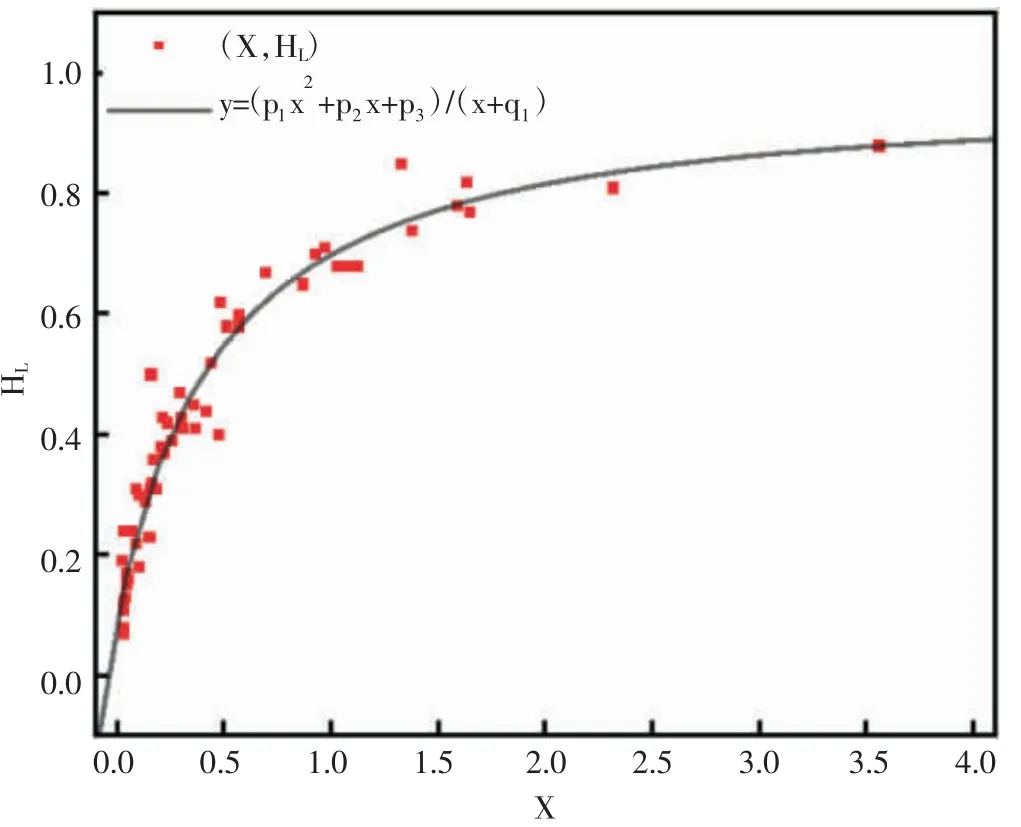
图1 数据点与曲线的对比图Fig.1 Comparison chart of data points and curves

通过对不同范围下的洛-马参数X 与Y 参数进行多项式拟合，得到了水平及微倾角与大倾角下的段塞流持液率预测模型。不同范围下的模型系数（见表4、表5），该模型的适用范围（见表6）。

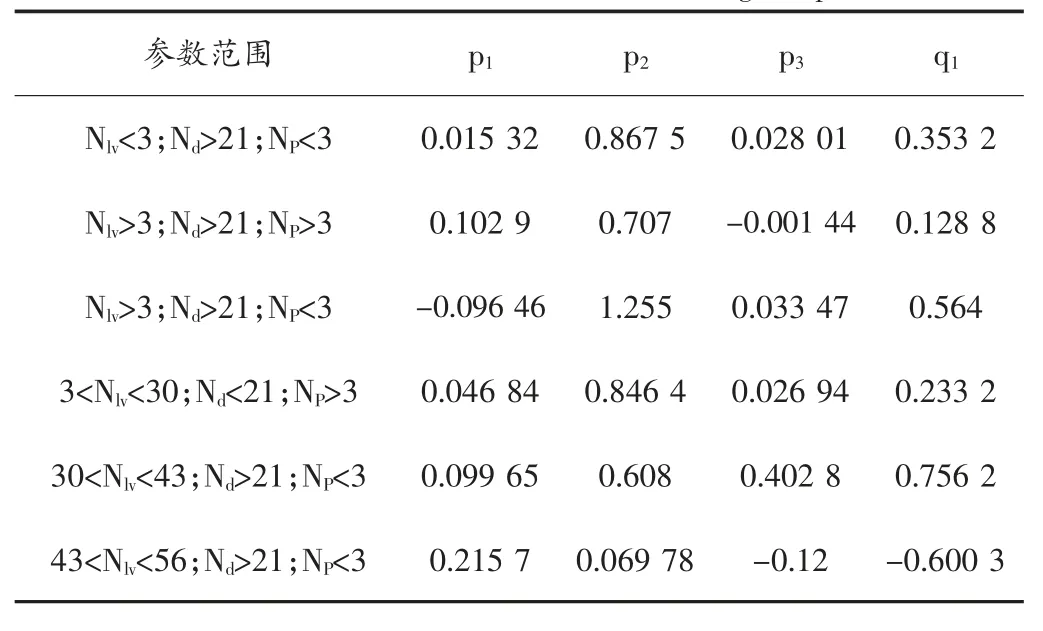
表4 水平及微倾角的模型系数Tab.4 Model coefficients of level and slight dip

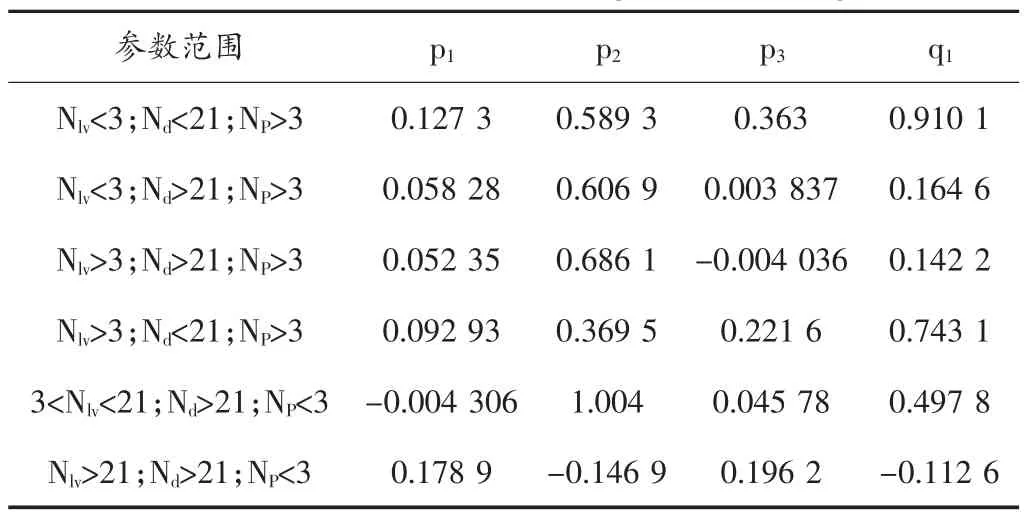
表5 大倾角下的模型系数Tab.5 Model coefficients under large inclination angle

表6 新模型的适用范围Tab.6 The scope of application of the new model

在水平及微倾角下持液率的预测公式为：

在大倾角下持液率的预测公式为：

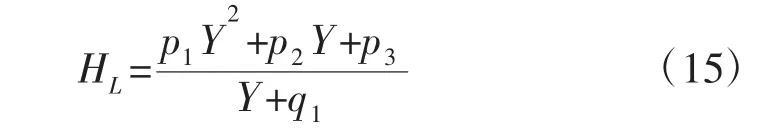
将段塞流持液率预测公式与表4 和表5 中的模型系数相结合，得到完整的段塞流持液率预测模型，该模型可以通过软件编程完成各特性条件下持液率的预测，程序流程（见图2）。

图2 程序流程图Fig.2 Program flow chart

4 模型预测

为了对新模型的准确性以及可行性进行评估，分别与Beggs-Brill[7]和Lockhart-Martinelli[15]提出的模型进行对比。三种模型预测对比结果（见图3），由图3 可以看出，Lockhart-Martinelli 模型在整个范围内预测结果较差，Beggs-Brill 模型在低持液率范围预测较好，在高持液率范围仍存在误差较大的情况，新模型的预测点大部分都在实际值附近，它在整个范围内预测效果都很好，由此可见，新模型的预测精确度更高。

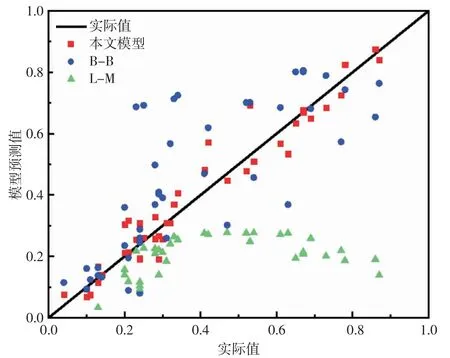
图3 三种模型的预测对比结果Fig.3 Comparison of the prediction results of the three models

为了更好地进行模型对比，采用Mandhane 等[19]提出的五种不同的误差测量方法来评估预测准确性。

（1）均方根误差：

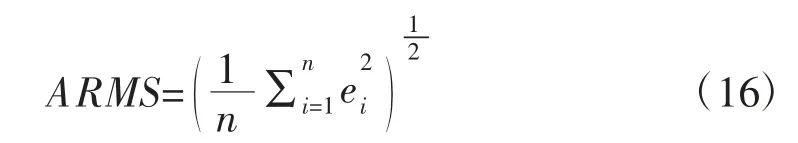
（2）平均百分比误差：

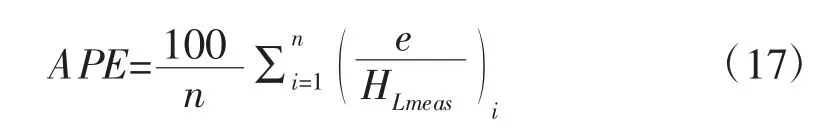
（3）平均绝对百分比误差：

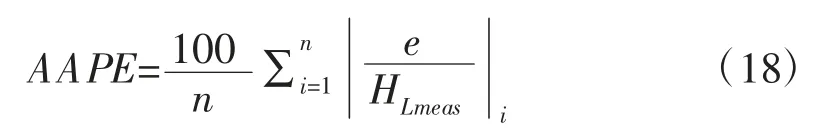
（4）绝对值平均绝对误差：

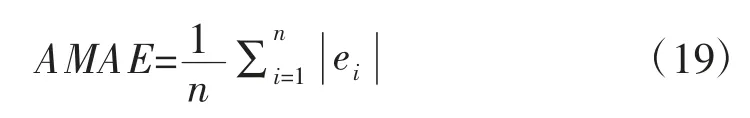
（5）平均绝对误差：

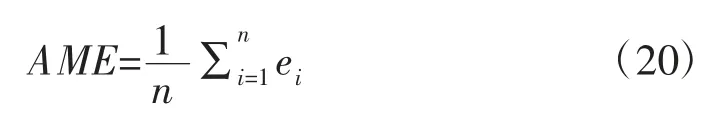
式中：ei-实际值与预测值的差值，ei=（HLpred-HLmeas）i，i=1，2，…，n。

三种持液率预测模型的误差对比（见表7），由表7可以看出，Beggs-Brill 模型相较于Lockhart-Martinelli模型，它在预测倾斜管道的持液率上的确具备较高的精确度，但是针对段塞流而提出的新模型的预测精确度还要高于Beggs-Brill 模型，误差均下降了40%以上。

表7 三种持液率预测模型误差对比Tab.7 Error comparison of three liquid holdup prediction models

综合以上两种对比分析方式，新模型用来预测精确度更高，可以用来预测段塞流持液率。

5 结论

（1）在持液率的预测中，分流型的预测是目前最为准确的，新模型采用Eaton 模型和Beggs-Brill 提出的倾斜校正系数结合的方式，对水平及微倾角0°＜θ≤10°和大倾角10°＜θ＜90°分别建立段塞流持液率预测模型，新模型具备Eaton 模型对参数适应性好的特点，同时也对大倾角下的段塞流持液率进行了修正。

（2）利用灰色关联度分析五大因素，得到各因素对持液率影响程度，顺序为：管径准数>归一化的压力>液体速度准数>液体黏度准数>气体速度准数。将前三种影响因素作为划分范围的标准，分别建立段塞流持液率预测模型，使得新模型具有范围针对性且预测精度更高。

（3）在划分范围后进行多项式拟合时发现，洛-马参数X 和Y 参数与持液率的数据点与多项式y=（p1x2+p2x+p3）/（x+q1）相关性极大，以此为基础可以准确得到不同范围下的段塞流持液率预测模型。新模型相较于Beggs-Brill 模型和Lockhart-Martinelli 模型，它预测段塞流持液率的精确度更高，应用范围更广。