基于ACE算法的水平管道持液率计算模型*

陈星杙 刘 伟 袁宗明 谢 英 贺 三

(1. 成都理工大学能源学院 四川成都 610059； 2. 西南石油大学石油与天然气工程学院 四川成都 610500)

持液率计算方法在水平管道两相流计算中占有重要地位，主要体现在[1]：①持液率与管内流体的物性有关；②持液率与管路流型紧密相关，如Taitel将持液率与管径之比为0.5作为环状流与段塞流的分界标准；③持液率与起伏管路的静压损失有关；④持液率对清管器的清管周期具有显著影响。但目前绝大部分的持液率计算模型均是由实验数据得出的经验或半经验相关式，具有一定的适用范围，如Lockhart-Martinelli相关式[2]仅适用于气液比较小的工况;Minami-Brill相关I式[3]则适用于持液率为0～0.35的水平管道等。为了建立适用范围更广、计算精度更高的水平管道持液率计算模型，本文通过对不同实验条件下的持液率实验数据进行收集与筛选，基于ACE(交替条件期望变换)算法[4-8]建立了适用于水平管道的持液率计算模型，并将该模型与已有的持液率计算模型进行对比，结果表明本文新建的持液率计算模型具有较高的计算精度，适用范围广，可为水平管道持液率计算提供借鉴。

1 计算模型的建立

表1 部分文献中两相流持液率测试实验的实验介质及条件

统计了国内外研究学者已开展的气液两相流持液率实验研究的实验介质及测试条件，结果见表1。对所统计文献中的持液率实验数据进行筛选(筛选标准为：实验测得的气液两相管流中的持液率数据相互独立；实验测得的持液率为气液两相混输体系达到平衡之后的持液率)，得到了影响持液率大小的主要影响因素为：管径d、气相折算速度vsg、液相折算速度vsl、黏度μ、压力p、温度T等6个参量，基于ACE算法对上述6个影响因素进行回归分析，得出计算持液率的转换函数，即

(1)

对式(1)进行逆变换得出持液率的计算式为

(2)

依据上述数据样本筛选原则，共筛选出625组相互独立的适用于水平管道的实验数据，其文献来源及相关实验条件见表2。从625组实验数据中随机选取325组用于持液率计算模型的建立(学习样本)，剩余的300组则用于持液率计算模型的验证(验证样本)。

水平管道各个影响因素与ACE最优变换函数之间的关系如图1所示。由图1a可知，随着管径的增加，变换函数逐渐下降；由图1b可知，当气相折算速度小于10 m/s时，随着气相折算速度的增加，变换函数快速下降，当气相折算速度大于10 m/s时，变换函数的下降速度变缓；图1c中液相折算速度与变换函数之间的关系变化趋势与图1b的正好相反，即当液相折算速度小于0.1 m/s时，随着液相折算速度的增加，变换函数上升速度较快，当液相折算速度超过0.1 m/s时，上升趋势变缓；由图1d、e可知，随着液相黏度与温度的增加，其分别对应的变换函数均呈现下降趋势；由图1f可知，当压力大于0.4 MPa时，随着压力的增加，其变换函数总体呈现上升趋势。分析发现，上述各影响因素与变换函数的关系曲线与各影响因素对持液率的影响规律研究结果基本一致，验证了采用ACE算法建立持液率计算模型的可行性。

表2 部分文献中两相流持液率的相关实验测试数据

图1 水平管道各个影响因素与本文基于ACE算法建立的最优变换函数之间的关系

图2 本文建立的持液率最优变换函数与各影响因素最优变换函数总和的关系

本文建立的持液率最优变换函数与各个影响因素最优变换函数总和的关系如图2所示。由图2可知，持液率最优变换函数与各个影响因素最优变换函数总和之间基本呈线性关系且二者多项式拟合曲线的斜率为1，可见二者满足式(1)相等关系，故本文建立的持液率计算模型正确。

持液率最优变换函数与持液率实验结果(学习样本)的关系如图3所示。根据多项式拟合结果，再综合考虑管径、气相折算速度、液相折算速度、压力、温度与黏度等影响因素，建立了水平管道两相流持液率计算模型：

H1=0.150 94+0.140 83S+0.026 26S2-

0.002 26S3-1.402 89×10-4S4

(3)

其中

(4)

式(3)、(4)中：S为各影响因素最优变换函数的总和；φi*(xi)为各影响因素对应的最优变换函数；aij为拟合系数，详见表3。

图3 本文建立的持液率最优变换函数与持液率实验结果(学习样本)的关系图

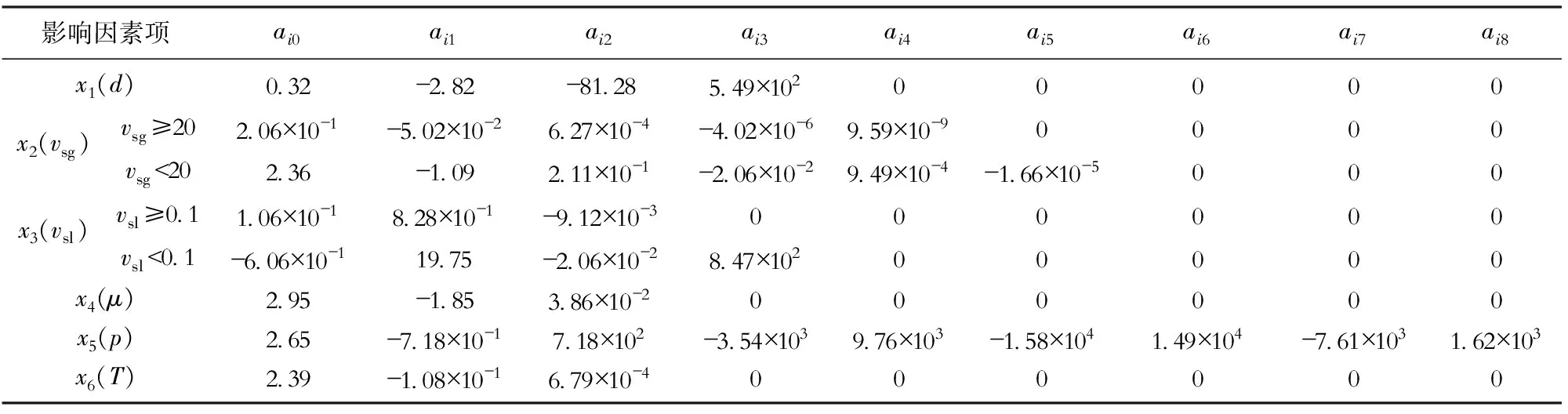
影响因素项ai0ai1ai2ai3ai4ai5ai6ai7ai8x1(d)0 32-2 82-81 285 49×10200000x2(vsg)vsg≥202 06×10-1-5 02×10-26 27×10-4-4 02×10-69 59×10-90000vsg<202 36-1 092 11×10-1-2 06×10-29 49×10-4-1 66×10-5000x3(vsl)vsl≥0 11 06×10-18 28×10-1-9 12×10-3000000vsl<0 1-6 06×10-119 75-2 06×10-28 47×10200000x4(μ)2 95-1 853 86×10-2000000x5(p)2 65-7 18×10-17 18×102-3 54×1039 76×103-1 58×1041 49×104-7 61×1031 62×103x6(T)2 39-1 08×10-16 79×10-4000000

2 计算模型的验证及适用范围

2.1 计算模型的验证

采用实验数据中的300组验证样本对ACE最优变换得出的持液率计算模型进行精确度验证，结果如图4、5所示。由图4、5可知，持液率模型计算值基本等于实验值，两者的绝对误差基本分布在±0.1的范围内，计算结果精度较高。

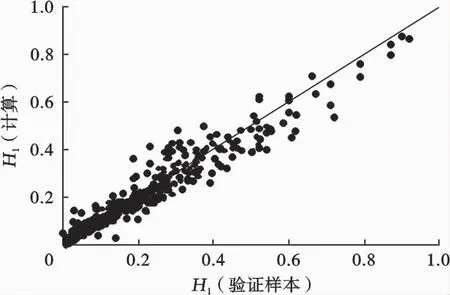
图4 持液率实验结果与本文计算结果的对比

图5 本文持液率预测结果误差分布(验证样本)

相关式名称持液率的计算公式适用条件Eaton相关式[1，22]H1=ΨN0 575lwNgwN0 0277dppb()0 05N1N1b()0 1[]Nlw=vslρ1gσæèçöø÷0 25，Ngw=vsgρ1gσæèçöø÷0 25，N1=μ1gρ1σ3()0 25，Nd=dgρ1σ()0 5水平管道的持液率计算Lockhart⁃Martinelli相关式[2，23](LM)H1=1-exp[-0 00883826(lnX)3-0 0289274(lnX)2-0 105733lnX-0 255216]X=vslvsg()78ρlρgæèçöø÷38μlμgæèçöø÷18气液比较小的水平管道Minami⁃Brill相关I式[3](MBI)H1=-0 0095+3 698X-11 497X2+65 22X4 X=H0 8945nslN0 0796pdN0 4076lw，Hnsl=vslvsl+vsg持液率为0～0 35的水平管道Minami⁃Brill相关II式[3](MBII)H1=1-exp{-[(lnZ+9 21)/8 7115]4 3374} Z=1 84N0 575lwNgwN0 0277pdppb()0 05N0 11持液率为任何大小的水平管道Abdul⁃Majeed相关式[15](AM)(H1)true=CH1，C=0 528(vsgvsl)-0 216121层流：H1=exp(-1 1+0 6788R-0 001232R2-0 001779R3+0 001627R4)紊流：H1=exp(-0 905+0 5286R-0 0922R2+0 00092R4)R=lnX，X=vsgρgμ1vslρlμgæèçöø÷mvsl2ρ1vsg2ρg，层流：m=1 0，紊流：m=0 2流型为层流与紊流的水平管流Mukherjee⁃Brill相关式[24](MB)H1=expC1+C2sinθ+C3sin2θ+C4N21()NgwC5NlwC6éëêêùûúúC1～C6：与管道倾角及流型相关的系数倾角范围为30°～75°的高气液比两相管流Beggs⁃Brill相关式[9](BB)H1(θ)=φH1(0)，H1(0)=a1Ea21Fra3，E1=Q′1Q′g+Q′1，Fr=v2mgdφ=1+C[sin(1 8θ)-13sin3(1 8θ)]C=(1-E1)ln(a4E1a5Nlwa6Fra7) a1～a7：与流型相关的系数任何倾角范围的两相管流，但结果可能出现负值，需进行校核

为了进一步验证本文采用ACE算法建立的持液率计算模型的计算精度，现将该模型与目前常用的7种持液率计算模型(表4)进行对比分析，任意选取表2中的45组持液率实验数据进行计算值和实验值平均相对偏差ARD(式5)、标准偏差SD(式6)的误差分析[21]，结果如图6、表5所示。由图6、表5可知，不同计算模型对应的计算精度差异较大，本文新建的持液率计算模型计算平均相对偏差最小(2.62%)、标准偏差最小(3.25%)，具有较高的计算精度。

(5)

(6)

图6 不同持液率计算模型持液率实验值与计算值的对比

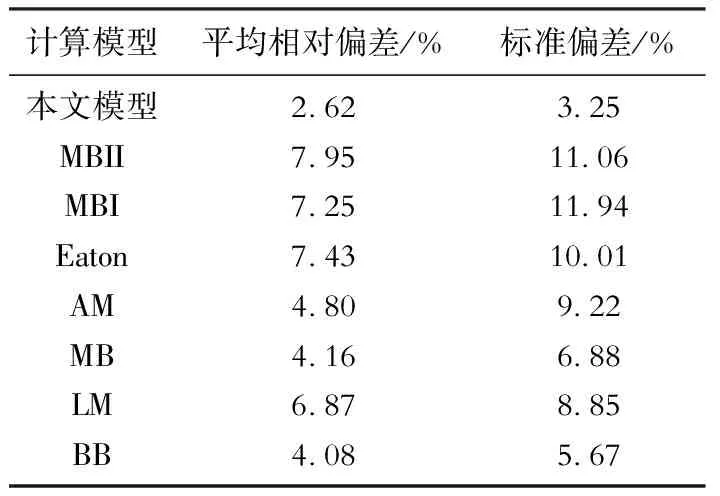
计算模型平均相对偏差/%标准偏差/%本文模型2 623 25MBII7 9511 06MBI7 2511 94Eaton7 4310 01AM4 809 22MB4 166 88LM6 878 85BB4 085 67

2.2 新建持液率计算模型的适用范围

根据Coleman等[25]和Grassi等[26]的研究结果可知：①当管道直径大于10 mm时，管道尺寸的增加对于管内流型的影响较小；②当管道长径比大于200时，管道内流动属于充分发展流动。同时，由DE等[27]的研究结果得出：只要Eo数(Eo=(2π)2γ/(Δρgd2))大于1，管内两相流均为充分发展流动。结合表1中的实验数据条件可知，本文选择的持液率实验数据均是大管内气液两相充分发展流动实验，因此，对于任何管径、管长条件下的管内气液两相流持液率计算均可适用；另外，管内两相受到重力、壁面剪切应力、气液界面剪切力的共同作用，符合实际生产中的动力学特性，遵循运动相似准则，因此采用ACE算法理论建立的持液率计算模型对于其他管径、管长条件下的管内两相流持液率计算仍然适用。

3 结论

综合考虑管径、气/液相折算速度、压力、温度以及黏度，基于ACE算法建立了适用于水平管持液率计算模型，该模型能够对各影响因素对持液率的潜在影响行为进行描述，具有较高的准确度，适用范围广，可为水平管道持液率计算提供借鉴。

符号注释

Hl—持液率；

d—管道直径，m；

vsg—气相折算速度，m/s；

vsl—液相折算速度，m/s；

μ—黏度，mPa·s；

p—操作压力，kPa；

T—操作温度，℃；

H1exp—实验持液率；

H1cal—计算持液率；

H1exp,i—第i次实验持液率；

H1cal,i—第i次计算持液率；

Nlw—液相速度准数；

Ngw—气相速度准数；

Nl—液相黏度准数；

Nd—管道直径准数；

Nlb—15.5 ℃、0.101 325 MPa下水的黏度准数，取值为0.002 26；

ρg—气相密度，kg/m3；

ρl—液相密度，kg/m3；

μg—气相黏度，Pa·s；

μl—液相黏度，Pa·s；

Npd—MB相关I、II式中管道直径准数；

σ—液相的表面张力，N/m；

θ—管道倾斜角度，(°)；

pb—气相计量的基准压力，101 008.234 Pa；

vm—气液混合物速度，m/s；

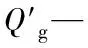
γ—界面张力，N/m；

Δρ—液相与气泡间的密度差，kg/m3。

[1] 喻西崇，赵金洲，冯叔初．起伏多相流管路持液率计算方法研究[J]．西南石油学院学报，2000,22(3)：94-97．

YU Xichong,ZHAO Jinzhou,FENG Shuchu.The prediction method of holdup in undulated multiphase pipelines[J].Journal of Southwest Petroleum Institute,2000,22(3):94-97.

[2] LOCKHART R W,MARTINELLI R C.Proposed correlation of data for isothermal two-phase,two-component flow in pipes[J].Chemical Engineering Progress,1949,45(1):39-48.

[3] MINAMI K,BRILL J P.Liquid holdup in wet-gas pipelines[J].SPE Production Engineering,1987,2(1):36-44.

[4] CHEN Xingyi,YUAN Zongming,ZHENG Yunping,et al.Prediction of carbon steel corrosion rate based on an alternating conditional expectation(ACE)algorithm[J].Chemistry and Technology of Fuels and Oils,2016,51(6):728-739.

[5] WANG D,MURPHY M J.Estimating optimal transformations for multiple regression using the ACE algorithm[J].Journal of Data Science,2004,25(2):329-346.

[6] SHOKIR E M.CO2-oil minimum miscibility pressure model for impure and pure CO2streams [J].Journal of Petroleum Science and Engineering,2007,58(1/2):173-185.

[7] BREIMAN L,FRIEDMAN J H.Estimating optimal transformations for multiple regression and correlation[J].Journal of the American Statistical Association,1985,80(391):580-598.

[8] MALALLAH A,GHARBI A R,ALGHARAIB M.Accurate estimation of the world crude oil PVT properties using graphical alternating conditional expectation[J].Energy & Fuels,2006,20(2):688-698.

[9] BEGGS H D.An experimental study of two-phase flow in inclined pieps[D].Tulsa:University of Tulsa,1972.

[10] PAYNE G A,PALMER C M,BRILL J P,et al.Evaluation of inclined pipe two-phase liquid holdup correlations using experimental data[D].Tulsa:University of Tulsa,1975.

[11] NGUYEN V T,SPEDDING P L.Holdup in two-phase,gas-liquid flow- II::experimental results[J].Chemical Engineering Science,1977,32(9):1015-1021.

[12] MUKHERJEE H.An experimental study of inclined two-phase flow[D].Tulsa:University of Tulsa,1979.

[13] ANDRITSOS N,NIKOLAOS.Effect of pipe diameter and liquid viscosity on horizontal stratified flow[D].Illionis:University of Illionis at Urbana-Champaign,1986.

[14] GUELER-QUADIR N.Two-phase pressure drop and holdup in flows through large diameter vertical tubing[D].Tulsa :University of Tulsa,1991.

[15] ABDUL-MAJEED G H.Liquid holdup in horizontal two-phase gas-liquid flow[J].Journal of Penolcum Scicnce and Enginecring,1996,15(2/3/4):271-280.

[16] BADIE S,HALE C P,LAWRENCE C J,et al.Pressure gradient and holdup in horizontal two-phase gas-liquid flows with low liquid loading[J].International Journal of Multiphase Flow,2000,26(9):1525-1543.

[17] 吕宇玲，杜胜伟，何利民，等．气液两相流持液率及压降特性的试验研究[J]．油气储运，2006,25(3)：48-51．

LV Yuling,DU Shengwei,HE Limin,et al.Study on the characteristics parameters of gas-liquid two-phase flow[J].Oil & Gas Storage and Transportation,2006,25(3):48-51.

[18] 徐继军．气液两相流倾斜下降管持液率实验研究[J]．石油工业技术监督，2009,25(4)：16-18．

XU Jijun.An experimental study on the liquid hold-up of gas-liquid biphasic tilted descending pipelines[J].Technology Supervision in Petroleum Industry,2009,25(4):16-18.

[19] 王乐．油气两相管流持液率变化试验研究[J]．石油天然气学报(江汉石油学院学报)，2015,37(7/8)：40-43．

WANG Le.Experimental study on change of liquid holdup in the oil-gas two-phase tubes[J].Journal of Oil and Gas Technology,2015,37(7/8):40-43.

[20] AI-RUHAIMANI F,PEREYRA E,SARICA C.Experimental analysis and model evaluation of high-liquid-viscosity two-phase upward vertical pipe flow[J].SPE Journal,2016：1-24.

[21] LI Zhaomin,WANG Shuhua,LI Songyan,et al.Accurate determination of the CO2-Brine interfacial tension using graphical alternating conditional expectation[J].Energy & Fuels,2014,28(1):624-635.

[22] 张友波，李长俊，杨静，等.多相混输管线截面含液率计算方法选择[J].西南石油学报，2005，27(6)：83-87.

ZHANG Youbo,LI Changjun,YANG Jing,et al.Selection of sectional liquid holdup calculation method for shinan oil field certain mulitiphase mixture transportation pipeline[J].Journal of Southwest Petroleum Institute,2005,27(6):83-87.

[23] EATON B A,ANDREWS D E,KNOWLES C R，et al.The prediction of flow patterns,liquid holdup and pressure losses occurring during continuous two-phase flow in horizontal pipelines[J].Journal of Petroleum Technology,1967,19(6):815-828.

[24] MUKHERJEE H,BRILL J P.Liquid holdup correlations for inclined two-phase flow[J].Journal of Petroleum Technology,1983,35(5):1003-1008.

[25] COLEMAN J W,GARIMELLA S.Characterization of two-phase flow patterns in small diameter round and rectangular tubes[J].International Journal Heat and Mass Transfer,1999,42(15):2869-2881.

[26] GRASSI B,STRAZZA D,POESIO P.Experimental validation of theoretical models in two-phase high-viscosity ratio liquid-liquid flows in horizontal and slightly inclined pipes[J].International Journal of Multiphase Flow,2008,34:950-965.

[27] DE B,MANDAL T K,DAS G.Experimental studies on phase inversion in a small diameter horizontal pipe[J].Chemical Engineering Research and Design,2010,88(7):819-826.