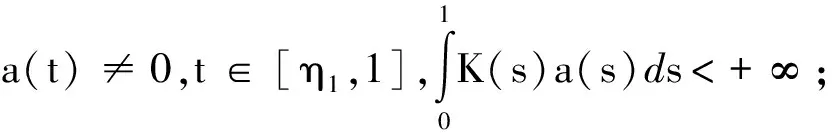奇异超线性和次线性n阶m点边值问题的非平凡解
谢 静
(沈阳化工大学 数理系, 辽宁 沈阳 110142)
在非线性常微分方程边值问题非平凡解存在性的研究中,很多作者在各种文献中对非线性函数赋予了各种条件,利用不同的理论获得了其非平凡解的存在性[1-11].在文献[4]中研究了n阶m点边值问题:


(H1)a:(0,1)→[0,+∞)连续且a(t)≠
(H2)f:(-∞,+∞)→(-∞,+∞)连续;
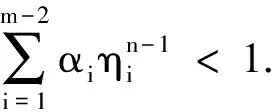
1 准备知识

K(t,s)=k1(t,s)+k2(t,s),
(3)
k1(t,s)=
引理2[4]令D<1,格林函数K(t,s)定义如式(3),则其满足:
(i)K(t,s)≥0连续,∀t,s∈[0,1];
(ii)K(t,s)≤K(s),∀t,s∈[0,1],并且存在常数γ>0,使得
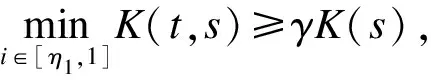
其中:当s=0时,K(s)=0;当s≠0时,
K(s)=k1(τ(s),s)+k2(1,s),
且K(s)≤A(1-s)n-1,其中
由引理2易知:
2) 当t∈[η1,1]时,γK(s)≤K(t,s)≤K(s),故0<γ≤1;
3) 当s=0,1时,K(s)=0;当s∈(0,1)时,K(s)>0.
P={u∈C[0,1],u(t)≥0,t∈[0,1]},
显然P是C[0,1]中的一个锥.令Br={u∈C[0,1],‖u‖
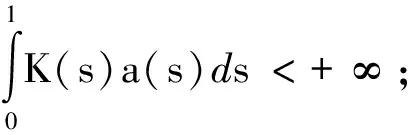
(H2)f:(-∞,+∞)→(-∞,+∞)连续;
设(Tu)(t)=

(4)
(Au)(t)=
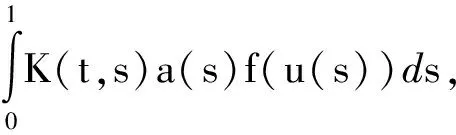
(5)
其中,K(t,s)定义如式(3).
引理3 假设(H1)、(H2)满足,则
A:C[0,1]→C[0,1]是全连续算子.
证明略.
很明显,如果算子A存在不动点u,则u是n阶m点边值问题(1)-(2)的解.
引理4 假设(H1)、(H2)都满足,则对于算子T(由式(4)定义)满足:
(i)T:C[0,1]→C[0,1]是全连续算子且T(P)⊂P;
(ii) 谱半径r(t)≠0且T存在一个相应于第一特征值λ1=(r(T))-1的正的特征函数.
证明方法类似于参考文献[2].



(i) 如果‖Au‖≥‖u‖,∀u∈∂Ω,则deg(I-A,Ω,θ)=0.
(ii) 如果θ∈Ω,‖Au‖≤‖u‖,∀u∈∂Ω,则deg(I-A,Ω,θ)=1.
2 主要结论
定理1 假设条件(H1)和(H2)满足,如果存在常数b≥0,使得
f(u)≥-b,∀u∈(-∞,+∞),
(6)
(7)
(8)
其中:λ1是算子T的第一特征值,则n阶m点边值问题(1)-(2)至少有一个非平凡解.
证明 由(7)式可知,存在r1>0,使
f(u)≥λ1|u|, ∀|u|≤r1.
(9)

0,t∈[0,1],

λ1(Tu)(t),t∈[0,1].
(10)
设A在∂Br1上没有不动点(否则,证明已完成).令u*是T的相应于λ1的正特征函数,即u*=λ1Tu*,下面证明:
u-Au≠μu*, ∀u∈∂Br1∩P,μ≥0.
(11)
如果存在u1∈∂Br1∩P和τ0≥0,使得u1-Au1=τ0u*,则τ0>0且u1=Au1+τ0u*≥τ0u*.令
τ*=sup{τ|u1≥τu*|},
(12)
很容易看出τ*≥τ0>0且u1≥τ*u*.又因为T(P)⊂P,则λ1Tu1≥τ*λ1Tu*=τ*u*.
由(10)式可得:u1=Au1+τ0u*≥λ1Tu1+τ0u*≥τ*u*+τ0u*=(τ*+τ0)u*.这与τ*的定义相矛盾,因此(11)式成立.

deg(I-A,Br1,θ)=
i(A,Br1∩P,P)=0.
(13)


f(u)≤σλ1u, ∀u≥r2.
(14)
设T1u=σλ1Tu,t∈C[0,1],则T1:C[0,1]→C[0,1]是有界线性算子且T1(P)⊂P.令

(15)
显然M<+∞.令
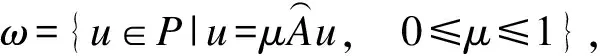
(16)
下面证明ω是有界的.


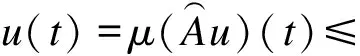


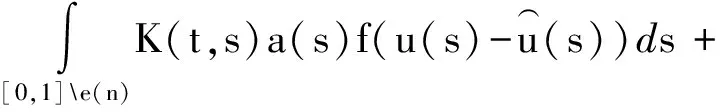
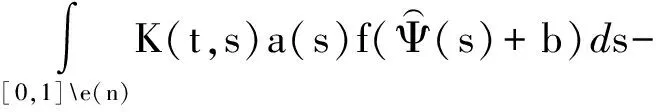


(T1u)(t)+M,
其中M由(15)式定义.因此((I-T1)u)(t)≤M,∀t∈[0,1].

又因为T1(P)⊂P,则(r(T1))-1(P)⊂P,因此有u(t)≤(I-T1)-1M,t∈[0,1],并且ω是有界的.
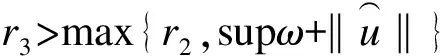
i(θ,Br3∩P,P)=1.
(17)

这是个矛盾.由拓扑度的同伦不变性及(17)式有:
deg(I-A,Br3,θ)=
deg(I-H(0,·),Br3,θ)=
deg(I-H(1,·),Br3,θ)=
(18)
由(13)和(18) 式有:
deg(I-A,Br3,θ)-
deg(I-A,Br1,θ)=1.

故n阶m点边值问题(1)-(2)至少有一个非平凡解.
定理2 假设条件(H1)和(H2)满足,如果存在常数b≥0,使得
f(u)≥-b,∀u∈(-∞,+∞);
(19)
(20)
(21)
其中λ1是算子T的第一特征值,则n阶m点边值问题(1)-(2)至少有一个非平凡解.
证明 由(21)式可知,存在ε>0,当u足够大时,使得f(u)≥(λ1+ε)u.
由(19)式可知,存在b1>b≥0,使得
f(u)≥(λ1+ε)u-b1,∀u∈(-∞,+∞).
(22)
令R1>
其中γ由引理2给出.
令u*是算子T相应于第一特征值λ1的正特征函数,则
u*=λ1Tu*.
(23)
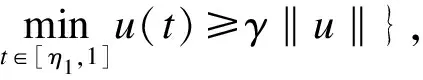



从而T(P)⊂P1.由(23)式可知,u*∈P1.假设A在∂BR1上没有不动点(否则,已证).
下面证明:
u-Au≠τu*,∀u∈∂BR1,τ≥0.
(24)
若存在u1∈∂BR1,τ1>0,使得u1-Au1=τ1u*.
由(22)式可知:
τ1u*(t).
(25)
因为b1>b>0,故f(u1(s))+b1>0.又因为T(P)⊂P1,u*∈P1,则
(26)
由(22)、(26)式及引理2得:
从而由(25)、(26)式可知:
(27)
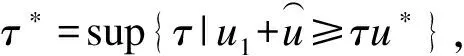
(28)
由引理7可知:
deg(I-A,BR1,θ)=0.
(29)
由(20)式可知,存在0 定义T1u=λ1Tu,u∈[0,1],故|(Au)(t)|≤λ1(Tu)(t)=(T1u)(t),即 |Au|≤T1u (30) 且T1:C[0,1]→C[0,1]是线性全连续算子,T1(P)⊂P,r(T1)=1. 下证Au≠τu,∀u∈∂BR2,τ≥1. (31) 否则,若存在u2∈∂BR2,τ2≥1,使得Au2=τ2u2,假设τ2>1(若τ2=1,得证). 由引理8可知: deg(I-A,BR2,θ)=1. (32) 由(27)和(32)式,有 deg(I-A,BR1,θ)- deg(I-A,BR2,θ)=0-1=-1. 定理3 假设条件(H1)~(H3)都满足,如果存在常数b≥0,使得 f(u)≥-b, ∀u∈(-∞,+∞), (33) (34) 其中λ1是T的第一特征值,如果存在r0>0,使得f(u)<ηr0,-r0 (35) 则n阶m点边值问题(1)-(2)至少有一个非平凡解. 证明:由(33)式可知,存在0 由(34)式可知,存在ε>0,R1>r0,当u>R1时,f(u)≥(λ1+ε)u. 假设A在∂Br1和∂BR1上没有不动点(否则已证). 由(13)式可知: deg(I-A,Br1,θ)=0. 另外由定理2及(29)式可知: deg(I-A,BR1,θ)=0. ∀u∈∂Br0,由(35)式和引理2可知: 则‖Au‖≤‖u‖.由引理9得deg(I-A,Br0,θ)=1,因此 deg(I-A,Br1,θ)=1; deg(I-A,Br0,θ)=1. 受文献[1-3]的启发讨论了奇异超线性和次线性n阶m点边值问题,即 在满足(H1)(H2)(H3)的条件下,结合线性全连续算子的第一特征值条件,运用锥上的拓扑度理论,得出非平凡解存在的结果.其中 (H2)f:(-∞,+∞)→(-∞,+∞)连续; 这里允许a(t)在t=0和t=1奇异且f不必是非负的,这一工作可看作是文献[4-5]相应n阶m点边值问题正解存在性结论的推广.下一步的工作设想:假设条件(H1)~(H3)满足,如果存在常数b≥0,使得 f(u)≥-b,∀u∈(-∞,+∞), 其中λ1是算子T的第一特征值,用拓扑度理论研究n阶m点边值问题(1)-(2)至少有两个非平凡解. 参考文献: [1] Cui Y J,Zou Y M.Nontrivial Solutions of Singular Superlinearm-point Boundary Value Problems[J].Applied Mathematics and Computation,2007,187(2):1256-1264. [2] Sun J X,Zhang G W.Nontrivial Solutions of Singular Sublinear Sturm-Liouville Problem[J].J Math Anal Appl,2007,326(1):242-251. [3] Zhang G W,Sun J X.Nontrivial Solutions of Singular Superlinear Sturm-Liouville Problem[J].J Math Anal Appl,2006,313(2):518-536. [4] Pang C C,Dong W,Wei Z L.Green’s Function and Positive Solutions ofnth Orderm-point Boundary Value Problem[J].Applied Mathematics and Computation,2006,182(2):1231-1239. [5] Yang J B,Wei Z L.Positive Solutions ofnth Orderm-point Boundary Value Problem[J].Applied Mathematics and Computation,2008,201:715-720. [6] Xian X.Positive Solutions for Singular Semi-position Three-point Systems[J].Nonlinear Anal,2007,66(4):791-805. [7] 郭大钧.非线性泛函分析[M].山东:科学技术出版社,2003:31-47. [8] 谢静.非线性奇异n阶m点边值问题的非平凡解[D].沈阳:东北大学理学院,2009:7-26. [9] 刘小会.非线性半正(k,n-k)共轭边值问题的非平凡解[D].沈阳:东北大学理院,2008:3-20. [10] 崔玉军.非线性算子与微分方程边值问题的多解[D].山东:山东大学,2006:10-15. [11] 孔慧.奇异(k,n-k)边值问题的解和多重正解[D].沈阳:东北大学理学院,2008:13-20.

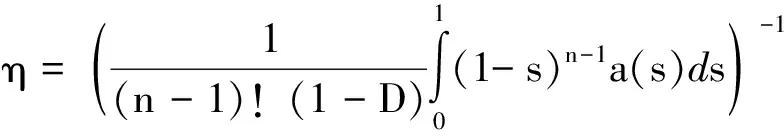


3 结 论