基于有限元法的转轴裂纹故障诊断研究

史久志， 宋栋亮， 李 胜， 李德慧， 张 宇， 王立鹏

(1.沈阳化工大学 能源与动力工程动学院, 辽宁 沈阳 110142； 2.天津化工厂 天泰化工公司, 天津 300480)

裂纹故障是转子系统后果最严重而又最难及时发现的故障，对转子系统安全运行产生巨大威胁.目前，如何开发和应用定量诊断方法，并与各种定性诊断方法相结合，既能诊断故障的种类，又可以诊断故障的位置和严重程度，从而为机械故障的监控和寿命评估提供依据，是研究的重要课题和发展方向.

目前，许多学者使用有限元方法对转轴裂纹进行分析.Dirr[1-2]和Iman[3]基于有限元法计算了在不同开闭状态下裂纹轴段的柔度.Ratan S等[4]采用有限元法离散模型，对该方法的鲁棒性进行灵敏度方法分析，实现在线识别转子裂纹位置.Sekhar[5]采用有限元方法分析了双裂纹转子系统的识别问题，将裂纹对转子的影响等效为无裂纹转轴上的附加载荷，可识别裂纹的位置与深度.Kim[6]基于有限元方法在考虑裂纹位置的情形下建立了多自由度裂纹转子模型，并用定向光谱研究了不同裂纹位置对裂纹导致的谐波响应的影响.Chasalevris和Papadopoulos[7]以裂纹的深度、位置和相对角度对裂纹进行识别.他们首次在裂纹轴旋转裂纹使用复杂的计算方法，在开裂表面对应变能密度函数进行积分，计算带裂纹的弯曲转子的复杂矩阵.陈雪峰、何正嘉[8]等从线弹性断裂力学的角度考虑裂纹引起的局部附加柔度，进而构造了小波有限元裂纹刚度矩阵，他们提出了基于小波有限元的裂纹故障诊断算法，克服了裂纹奇异性给传统有限元算法造成的困难.将系统前三阶的固有频率作为输入，绘制裂纹等效刚度与裂纹位置的3条曲线，根据曲线的交点可以预测出裂纹的位置与尺寸.向家伟、陈雪峰、何正嘉[9]等提出了一种基于神经网络的短粗转子系统横向裂纹定量识别的区间B样条小波有限元方法.

本文首先建立转轴有限元模型，然后通过有限元求解不同裂纹位置和深度及对应的固有频率，将其作为BP神经网络的学习样本,对神经网络进行训练,并将不同工况下转轴固有频率代入训练好的网络,诊断出裂纹的位置和深度.研究表明：本文所提出的裂纹诊断方法神经网络精度高，稳定性强,易于在工程实践中进行转轴裂纹定量诊断.

1 转轴裂纹有限元分析

转轴长度分别为L=3 000 mm，转轴直径d=375 mm，E=2.06×1011N/m2，ρ=7 800 kg/m3,泊松比μ=0.3.裂纹深度分别取为裂纹直径的20 %、40 %、60 %、80 %；位置分别取为0.3、0.6、0.9、1.2、1.5、1.8、2.1、2.4、2.7 m.

用有限元分析软件ANSYS编制数值方法的计算程序，对不同位置、不同深度下转轴裂纹的固有频率和振型进行计算.中间位置裂纹转子前三阶固有频率值如表1所示.根据计算结果，得到裂纹参数与固有频率之间的关系，为裂纹结构的精确建模与仿真奠定了坚实的理论基础.图1给出部分计算结果：位置中间x=1.5 m，裂纹径向深度为裂纹直径的20 %.

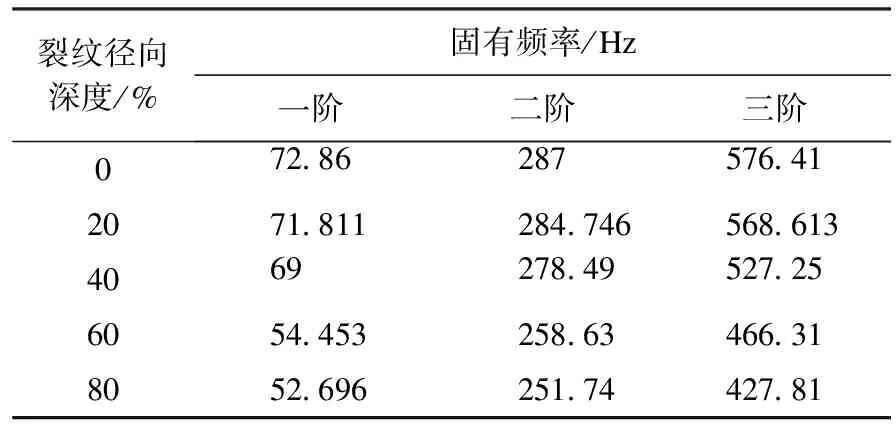
表1 中间位置(x=1.5 m)不同裂纹径向深度对应的固有频率

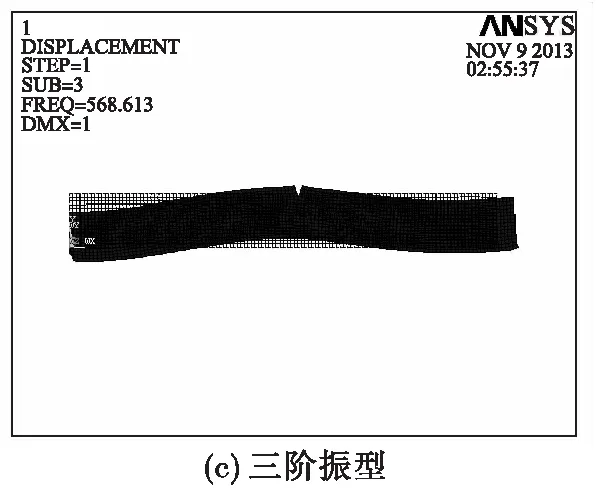
图1 转轴裂纹前三阶振型图

2 基于BP神经网络的裂纹故障诊断

BP(Back Propagation)神经网络，简称误差反向传播神经网络，是一种神经网络学习算法.由输入层、隐层、输出层组成神经网络，隐层可扩展为多层.相邻层之间各神经元进行全连接，而每层各神经元之间无连接.网络按有教师的方式进行学习，各神经元获得网络的输入产生连接权值(Weight).然后按减小希望输出与实际输出误差的方向，从输出层经各中间层逐层修正各连接权值，回到输入层.此过程反复交替进行，直至网络的全局误差小于给定值，即完成学习的过程.其结构如图2所示.

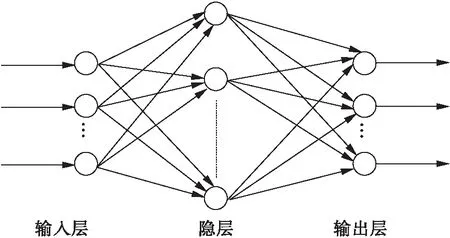
图2 BP神经网络模型

作为一种先进的智能计算方法，神经网络既具有强大的非线性逼近能力，又特别适用于输入输出关系不明确或结果形成不明确的问题，因此，利用BP神经网络可以逼真地描述频率与裂纹之间的关系.

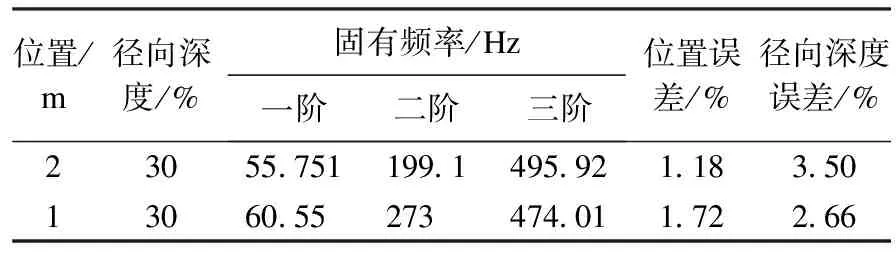
以裂纹不同位置、深度和对应的一阶、二阶、三阶固有频率作为BP神经网络的学习样本，对BP神经网络进行训练，并将不同工况下的固有频率输入训练后的神经网络，定量地诊断出裂纹参数.其中，学习率设为0.01，训练误差设为0.001，输入节点数为37个，隐层节点数为25个.图3为BP神经网络训练误差与迭代次数关系图，大约训练2 500次完成训练.表2为转轴横向裂纹工况及诊断结果.结果表明：该网络具有较高的精度，转轴裂纹位置误差小于转轴长度的2 %,而裂纹深度误差小于转轴直径的4 %.

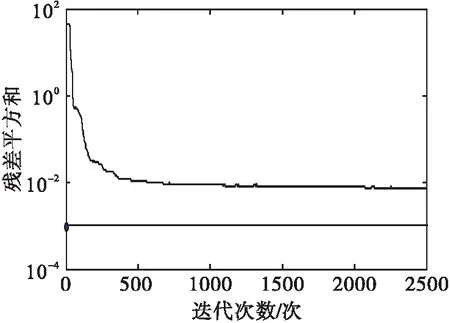
图3 BP神经网络训练误差与迭代次数关系

位置/m径向深度/%固有频率/Hz一阶二阶三阶位置误差/%径向深度误差/%23055.751 199.1495.921.183.5013060.55273474.011.722.66

从神经网络训练的结果发现：对出现在距转轴两端0.3 m内的裂纹，识别的效果相对较差，这主要是端部裂纹转轴固有频率随裂纹深度变化不敏感造成的.另外，过浅的裂纹由于固有频率的变化较小，识别起来也比较困难；通常裂纹径向深度在10 %以内的裂纹，识别起来效果较差.

3 结 论

基于有限元方法建立转子系统的模型，并用BP神经网络对横向裂纹进行定量识别.一方面,通过求解转轴有限元模型,获得不同裂纹位置和深度下的前三阶固有频率.另一方面,将不同裂纹位置和深度以及对应的转轴固有频率作为BP神经网络的学习样本,训练BP 神经网络,并将不同工况下转轴固有频率输入训练好的网络,实现对裂纹参数的定量诊断.结果表明裂纹位置误差小于转轴长度的2 %,而裂纹深度误差小于转轴直径的4 %.今后，将以该研究结果作为依据，推广该方法在实际中的应用.

参考文献：

[1] Dirr B O,Schmalhorst B K.Crack Depth Analysis of a Rotating Shaft by Vibration Measurement[J].Journal of Vibration,Acoustics,Stress,and Reliability in Design,1988,110(2):158-164.

[2] Dirr B O,Popp K,Rothkegel W,et al.Detection of Small Transverse Cracks in Rotating Shafts[J].Archive of Applied Mechanics,1994,64:206-222.

[3] Iman I,Scheibel J,Azzaro S H.Development of an On-line Rotor Crack Detection and Monitoring System[J].Journal of Vibration,Acoustics,Stress,and Reliability in Design,1999,111(3):241-250.

[4] Ratan S,Baruh H,Rodriguez J.On-line Identification and Location of Rotor Cracks[J].Journal of Sound and Vibration,1996,194(1):67-82.

[5] Sekhar A S.Model-based Identification of Two Cracks in a Rotor System[J].Mechanical Systems and Signal Processing,2004,18(4):977-983.

[6] Kim J,Ewins D J.Effect of Crack Locations on the Vibration Characteristics of MDOF Rotor Systems[C]//Proceedings of the 25th International Conference on Noise and Vibration Engineering.Leuven:ISMA,2000:281-287.

[7] Chasalevris A C,Papadopoulos C A.Identification of Multiple Cracks in Beams under Bending[J].Mechanical Systems and Signal Processing,2006,20(7):1631-1673.

[8] 陈雪峰,李兵,胡桥,等.基于小波有限元的裂纹故障诊断[J].西安交通大学学报，2004,38(3):295-298.

[9] 向家伟,陈雪峰,何正嘉.基于神经网络的短粗转轴裂纹诊断研究[J].振动与冲击,2007,26(11):20-24.