基于标准粒子群算法对热工模型的辨识

吕丽霞，林向雨

(华北电力大学 控制与计算机工程学院，河北 保定071003)

0 引言

为设计一个优良的控制系统，必须充分了解被控对象、执行机构以及系统内一切元件的运动规律，即他们在一定的内外条件下所必然产生的相应运动。内外条件与运动之间存在的因果关系大部分可以用数学形势表示出来，这就是控制系统运动规律的数学描述，即所谓的数学模型。建立数学模型的过程就是系统建模的过程。

系统建模的方法通常有两种，一种是白盒法，也就是机理建模，其在对系统的机理有了详细的了解之后，才可能得出系统的数学模型。另一种是黑盒法，也就是系统辨识，其认为系统的动态特性必然表现在这些输入与输出的数据中［1］。具体的方法是:对一个系统加入不同的扰动信号，观察其输出，根据所记录的输入输出信号，估算出表达这个系统的输入与输出关系的一个数学模型。黑盒和白盒法都有各自的优缺点，可以将这两种方法结合起来，形成一种新的方法——灰盒法。主要做法是:当通过其内在机理分析出系统的数学模型结构时，就可以把系统辨识的问题简化成参数辨识的问题，再把参数辨识问题转化成参数优化的问题，实际上就是函数拟合的问题［1］。

现在更多的是采用智能算法去研究系统辨识，其中粒子群算法是智能算法中研究最多的一种方法。下面主要采用粒子群算法中的标准粒子群算法对火电生产过程中蒸汽变化量对汽包水位的影响的传递函数以及送风量和引风量变化对炉膛负压影响的传递函数进行辨识。

1 粒子群算法

粒子群算法是一种基于种群智能方法的演化计算技术，其易实现、通用性强、收敛速度快等特点越来越受到研究者的青睐。该方法一经提出，研究甚多，得到了很多改进，同时也取得了不错的效果。

从20 世纪90 年代初，就产生了模拟自然生物群体行为的优化技术。粒子群优化算法(Particle Swarm Optimization，PSO)是Eberhart 和Kennedy 受鸟类捕食行为的启发而提出的仿生优化算法［2］。设想有一群鸟在随机搜寻一块食物，找到食物的最简单有效的方法就是搜寻距离食物最近的鸟的周围区域。PSO 算法是一种较好的全局优化算法，它主要用于优化复杂的非线性函数，稍加修改也可以用来解决组合优化的问题。粒子群算法不需要被优化函数可微、可导，甚至不要求知道被优化函数的具体表达式，只要通过编程得到被优化函数的适应度，此方法就是适用的［1］。

1.1 PSO 的基本思想

PSO 的基本思想是把每一个优化问题的解都当作是搜索空间的粒子，所有的粒子都有一个被优化函数的适应值(Fitness Value)，每个粒子还有一个速度向量决定他们飞翔的方向和距离，然后粒子们追随当前的最优粒子在解空间中进行搜索［3］。

在PSO 算法中，首先随机产生一群粒子(初始速度、位移、以及其决定的适应度值都应该随机化)，每一个粒子都是搜索空间的可能解，然后通过迭代寻找最优解。假设群体中每个粒子可以互相通信，每个粒子都能记住目前为止整个群体的最好位置。这样，每次迭代中粒子跟踪两个“极值”来更新自己:第一个极值是迭代后粒子本身目前的最优解，称为局部最优解xbesti;第二个极值是整个种群寻找过程中通过相互联系比较得出的最优解，称为全局最优解Xbestg，通过不停的迭代计算与优化最终会得到所期望的最优解［4］。

1.2 PSO 的实现方法

本文采用的标准粒子群算法，是对基本粒子群算法的一种改进。首先介绍一下基本粒子群算法的实现方法。以求目标函数Q(X)为例，对于最小化问题，目标函数值越小，对应的适应值就越好。

假设在一个N 维的目标搜索空间中(N 维相当于Q(X)中未知因子的个数，也就是优化参数的个数)，有m 个粒子组成的一个群体(即m组可能解)，将第i 个粒子表示为一个N 维的向量Xi=(Xi1，Xi2，…，Xin)，i=1，2，…，m;其速度也是一个N 维向量，记作Vi=(Vi1，Vi2，…，Vin)。速度决定粒子在搜索空间单位迭代次数的位移。随机产生一组Xi，作为第一代初始种群。将Xi代入目标函数Q(X)就可以计算出其适应值，根据适应值的大小来衡量Xi的优劣。设第i 个粒子迄今为止搜索到的最优位置为Xbesti=(Xi1，Xi2，…，Xin)，相应的适应值记为Qbesti，则粒子i 的当前最好位置可以表示

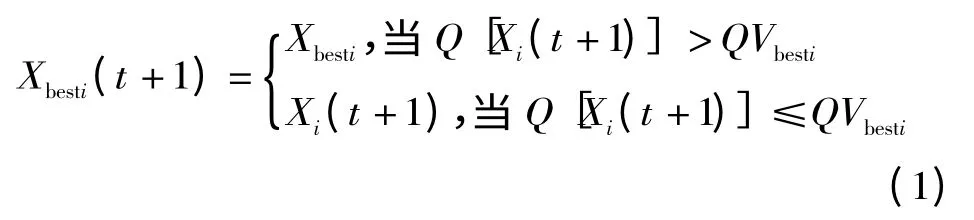
寻优过程中整个粒子群迄今为止搜索到的最优位置为Xbestg=(xg1，xg2，…，xgn)，其对应的适应值即全局最优解记为Qbestg。粒子根据以下公式来更新自己速度和位置。

其中，i=1，2，．．．，m，n=1，2，．．．，N;t表示第t 代。学习因子c1，c2是非负常数，r1和r2是介于［0，1］之间的随机变量。在速度更新的时候，不应该超出给定的速度范围，单步前进的最大值Vmax根据粒子的取值区间长度来确定。根据式(3)来更新位置向量［4～7］:

标准粒子群算法是指带惯性权重的粒子群算法。主要是在式(2)中引入了惯性权重w，详见式(4):

惯性权重w 是为了权衡全局搜索和局部搜索而引入的，惯性权重代表了原来速度在下一次迭代中所占得比例。w 较大时，前一速度的影响较大，全局搜索的能力比较强;w 较小时，前一速度的影响较小，局部搜索能力比较强。恰当的权重值在搜索速度和精度方面起着协调作用［5］。一般采用惯性权重递减策略，即在计算初期采用较大的权重来对全局进行搜索，后期则采用较小的权重值，这样有利于算法的收敛。

2 粒子群算法的系统辨识

粒子群算法辨识的具体步骤:

(1)根据采集来的数据画出系统的输入与输出关系的图像。

(2)估计模型的大概结构，给出模型的传递函数的大概形式，定义参数的个数以及辨识区间。

(3)利用粒子群算法对参数进行优化，得到最终优化后的参数。优化步骤如下:

a．初始化种群:定义初始种群，进化代数、种群速度的限幅、权重区间(这个种群必须是随机的)。

b．根据目标函数计算种群中各粒子的适应度，并对其进行评价，找出粒子的最优位置以及全局粒子的最优位置。

c．对种群中的各个粒子进行位置修正和速度限制。

d．对更新过的种群再次进行适应度计算，比较新的Xbest1和Xbestg，选取更好的解来进行判断是否符合要求，如果符合，则该解就是优化得到的最优解;如果没有满足，则继续对粒子速度和位置进行更新，直到满足要求或到达最大迭代次数为止。

利用粒子群算法进行系统辨识的具体流程图如图1 所示。

图1 粒子群算法系统辨识流程图

3 粒子群算法的仿真实现

现如今，国内大部分电厂大都引进分散控制系统和厂级监控信息系统，这样就可以为热工过程的模型辨识提供有用的数据信息，但是用于系统辨识数据的优劣选择决定了辨识结果的好坏［1］。因此，在对大量的现场数据进行遴选时需要注意:

(1)现代工业过程中都是多输入多输出的耦合系统，在选择时尽量选择多输入中的某一个输入对应系统的某一个输出进行辨识。

(2)采样数据要起始于某一个稳定的工况点，这样数据序列反应的就是某一稳定开始的动态过程，便于确定所采集数据的“零初始点”。

从现场采集来的数据通常含有高低频以及直流成分，会对辨识的精度产生一定的负面影响。因此，需要对数据进行预处理，通常采用的手段有数据滤波、零初始值和粗大值处理等方法。

3.1 粒子群算法对蒸汽变化对汽包水位影响的传递函数的辨识

已知某火电机组在100%负荷工况下得到的蒸汽量变化对应汽包水位变化的传递函数为:

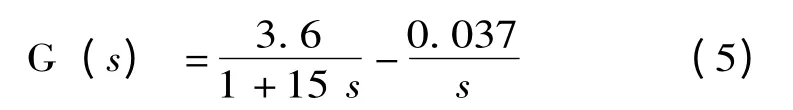
由Matlab 数学工具得到该系统在输入为单位阶跃下的响应曲线，将得到的数据记录下来，并且利用改进后的粒子群算法对其曲线进行辨识，得到该系统辨识的仿真结果如图2 所示。

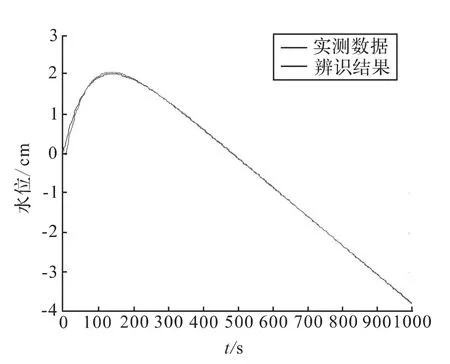
图2 辨识结果与采集数据的对比

辨识出该系统中蒸汽变化量对汽包水位的影响的传递函数是:

3.2 粒子群算法对送引风的变化对应炉膛负压影响的传递函数的辨识

某1 000 MW 超超临界火电机组，在90%负荷时，从现场SIS 数据中得到负荷发生变动后各变量的响应数据。并从中截取一段数据存放于文件uy- 900- 210- 8- 21．txt(该数据从文献［1］所附光盘中所得)中，利用粒子群优化算法辨识送引风量变化对炉膛负压的影响的数学模型，辨识仿真结果如图3 所示。

图3 辨识结果与采集数据的对比

辨识出送引风的变化量对炉膛负压的影响传递函数是:

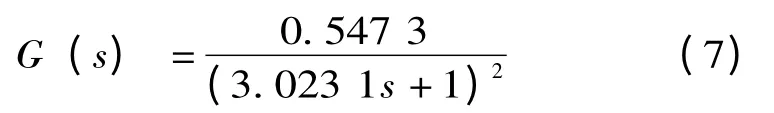
3.3 辨识结果分析

图2 中有两条曲线，其中一条是读取Matlab仿真结果所得的曲线，另一条表示经粒子群算法辨识后得出的系统在单位阶跃响应下的曲线，可以看出两条曲线几近重合，说明利用粒子群算法辨识所得的结果具有一定的准确性;图3 中虚线是读取由现场SIS 系统采集得到的原始数据所得到的曲线，实线是经粒子群优化算法辨识后得出的模型在单位阶跃响应下的曲线，可以看出这两条曲线还是比较接近的，说明利用粒子群算法辨识得到的模型具有一定的参考价值。

4 结论

采用粒子群算法辨识出的两个火电厂生产过程中的系统模型对火电厂的研究具有一定的参考价值。利用粒子群算法对系统模型进行辨识时，借用了群体智能的思想，不需要知道该系统内部的具体结构，只需要对假设的该系统的结构参数进行优化，优化出理想的参数，即可得到该系统的数学模型。该方法具有智能优化算法的各种优点，是一种简单实用的智能辨识方法，可以用于一般的工业系统辨识中，为工业系统更准确的建模提供了有力的保障。

［1］韩璞．智能控制理论及应用［M］．北京:中国电力出版社，2012．74-99．

［2］聂琼．浅谈粒子群算法与BP 神经网络［J］．轻纺工业，2013，(1):68-70．

［3］焦嵩鸣，谭雨林，桑世杰．基于改进粒子群算法的主汽温控制系统PID 参数优化［J］．电力科学与工程，2012，28(12):9-13．

［4］王峰，邢科义，徐小平．系统辨识的粒子群优化方法［J］．西安交通大学学报，2009，43(2):116-120．

［5］王东风，韩璞，王国玉．锅炉汽包水位系统的预测函数控制［J］．华北电力大学学报，2003，30(3):44-47．

［6］董泽，丁方，桑世杰．基于PSO 算法的1 000 MW 机组主汽温系统辨识［J］．电力科学与工程，2012，28(12):1-5．

［7］王利杰，孙明，程希，等．循环流化床锅炉床温的传递函数智能建模方法［J］．电力科学与工程，2013，29(1):71-78．