谐振接地系统单相故障仿真与分析

吴丽娜，刘观起

(华北电力大学 电气与电子工程学院，河北 保定071003)

0 引言

中性点非直接接地系统，即变压器或发电机的中性点不直接接地系统，因短路电流小，又称小电流接地系统。小电流接地系统接地方式主要包括3 种，即中性点不接地、谐振接地(中性点经消弧线圈接地)和中性点经电阻接地［1］。从目前我国的配电网分布及发展规划情况看，谐振接地方式在这3 种接地方式中占有重要地位，是我国配电网主要的接地方式。

小电流接地系统单相接地故障时，相间电压仍保持对称，接地电流小，仅为线路及设备的电容电流，不影响对负荷的供电，允许继续运行1～2 h，在我国3～66 kV 配电网中得到广泛应用。但是系统中非故障相对地电压升高，当故障持续时间过长时容易破坏电网薄弱环节处的绝缘，从而形成两点或多点接地短路，破坏系统的安全稳定运行。运行人员应及时找到故障线路及故障发生点，并予以切除。尤其对于谐振接地系统，由于消弧线圈的补偿作用，使得发生单相故障时故障线路的电流幅值很小且方向不确定，增大了故障选线的难度。目前谐振接地系统的选线方法有五次谐波分量法、残流增量法、有功分量法以及能量法等［2～4］。近年来，有不少学者在研究应用小波理论实现故障选线，提出了不少分析方法，如离散小波变换法、小波包分析法以及基于小波变换的暂态零序电流比较法等，而这些选线方法的灵敏度和可靠性受故障距离、故障前初相角、过渡电阻等因素的影响较大［5］。研究在这些因素变动时谐振接地系统单相故障的稳态特征和暂态特征可为配电网谐振接地系统单相故障选线提供依据，目前国内外相关这方面的研究较少。

1 谐振接地系统单相故障的特点

谐振接地方式，即将一个电感(通常称作消弧线圈)接入到中性点和大地之间。当系统发生单相接地故障时，消弧线圈的电感电流对系统接地电容电流进行有效补偿，使流过接地点的电流减小，有助于熄灭残余电流的接地电弧，防止电弧进一步扩散。同时由于消弧线圈的补偿作用，使恢复电压的幅值和初速度降低，抑制了电弧的重燃及弧光接地过电压的产生，防止系统由单相短路故障进一步发展为更加严重的多相或相间短路故障，使系统的供电可靠性得到提高［6］。

当系统发生单相故障时，在中性点加设消弧线圈，补偿接地电容电流，可有效防止发生弧光间歇过电压。按规程规定，在各级电压网络中，当系统的电容电流超过一定数值(22～66 kV 电网超过10 A;10 kV 电网超过20 A;3～6 kV 电网超过30 A)时就应装设消弧线圈［7］。

在谐振接地系统中，单相故障时的电流分布如图1 所示，由于在电源的中性点接入了消弧线圈，当线路A 相接地以后，相比中性点不接消弧线圈，电容电压的大小和分布都不变，但在接地点增加了一个电感分量的电流，因此，从接地点流回的总电流为

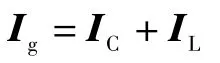
式中:IC为全系统的对地电容电流;IL为流过消弧线圈的电感电流，若用L表示电感，则

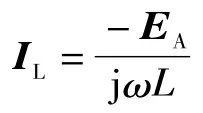
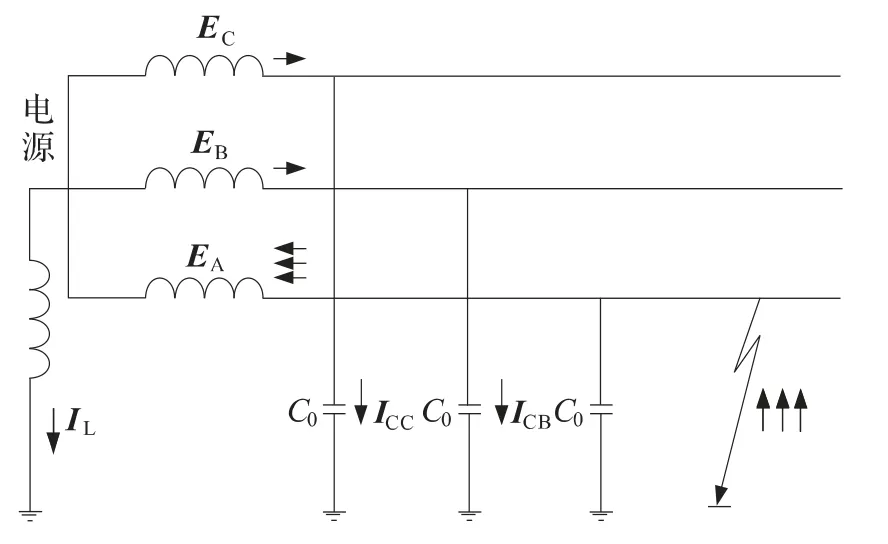
图1 谐振接地系统A 相故障时的简化网络图

IL与IC方向相反，即由于消弧线圈的补偿作用，使接地点总电流Ig减小了。根据补偿程度的不同，消弧线圈的补偿方式可分为完全补偿、欠补偿和过补偿［8］。

完全补偿即电感电流IL与电容电流IC向量和为零的补偿方式。此时，电容电流IC与电感电流IL幅值相等，方向相反，彼此完全抵消，残余电流几乎为零，但由于此时电流谐振回路恰好在谐振点工作，如果发生断路器三相不同期合闸，则出现的零序电压将在串联谐振回路中产生很大的电流，进而在消弧线圈上产生危险的过电压，损坏设备和人身安全，所以一般不采用完全补偿方式。

欠补偿即电感电流IL小于电容电流IC的补偿方式。在该方式下，残余电流中除了含有有功电流分量外，还含有容性无功电流分量，当系统运行方式发生变化导致系统的容性无功电流分量减小时，可能恰好又变为完全补偿，因此也很少采用欠补偿方式进行补偿。

过补偿即电感电流IL大于电容电流IC的补偿方式。相比前两种方式，过补偿的优势是不会产生串联谐振过电压。即使电网扩大，对地电容电流有所增加，依然留有补偿裕度，所以过补偿是实际系统广泛采用的补偿方式，过补偿度一般取5%～8%。

2 仿真模型的搭建

在MATLAB 中建立谐振接地系统的仿真模型如图2 所示，系统频率设为50 Hz，微分方程解算方法采用odel5，该方法对求解病态方程效果良好。仿真开始时间为0，结束时间为0．2 s，其他仿真参数都选默认值。系统采用无穷大电源，变压器采用Three-phase Transformer(Two Windings)模型，变比为38．5/10．5 kV，YYO连接。共4 条线路，长度分别为:L1=70 km，L2=80 km，L3=90 km，L4=100 km。线路各序参数为:正序电阻R1=0．012 73 Ω/km，零序电阻R0=0．386 4 Ω/km;正序电感L1=0．933 7 e-3 H/km，零序电感L0=4．126 4e-3 H/km;正序电容C1=12．74 e-9 F/km，零序电容C0=7．751 e-9 F/km。

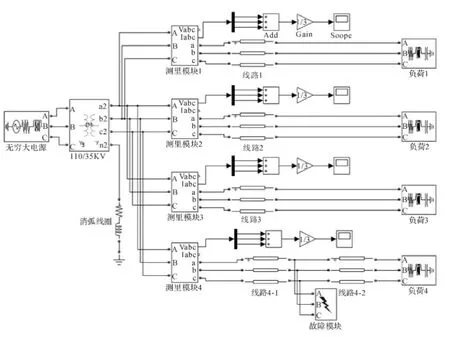
图2 谐振接地系统单相故障仿真模型

在各线路的首端、故障点和中性点均设有测量模块。当谐振接地系统发生单相接地故障时，特征量的暂态过程随故障距离、故障前初相角、过渡电阻的变化而变化，包含了多种频率成分的周期分量和非周期分量，由各测量模块测得并通过示波器显示波形［9］。

3 单相故障仿真及对比分析

3.1 故障距离对故障的影响仿真

保持故障初相角和过渡电阻不变，即φ=65°，Rg=50 Ω，分别在距离线路4 出口L=0，20，50，80 km 处进行A 相接地故障仿真，根据仿真结果得到不同故障距离L 下的故障量稳态幅值，故障特征量包括故障相母线残压Ucy、零序电压U0、非故障线路零序电流If0、故障线路零序电流Ig0以及接地故障电流Ijd，如表1 所示。限于篇幅，只列出当L=20，50，80 km 时零序电压和故障线路零序电流波形，以便观察波形变化趋势，如图3，4，5 所示。

表1 不同故障距离下的故障量稳态幅值

图3 故障距离为20 km 时的故障特征量波形

图4 故障距离为50 km 时的故障特征量波形

图5 故障距离为80 km 时的故障特征量波形

由表1 中数据可知，随着故障距离的增加，由于线路压降也增加，故障相的残余电压有所升高。其他故障量的稳态值略有下降，但总体看来，故障距离的变化对其影响不大。

由图可看出，故障距离的改变对暂态过程有较大影响。随着故障距离的增加，各故障量的暂态冲击值、暂态波动随之减小，而暂态分量衰减速度随之增大。

3.2 故障初相角对故障的影响仿真

改变故障发生时刻即可改变故障初相角。保持故障距离、过渡电阻不变，即L=20 km，Rg=50 Ω，分别在故障初相角 φ 为90°，180°，270°的条件下进行仿真，零序电压、非故障线路零序电流以及故障线路零序电流随故障初相角的波形变化规律如图6，7，8 所示。

图6 故障初相角为90°时的故障特征量波形

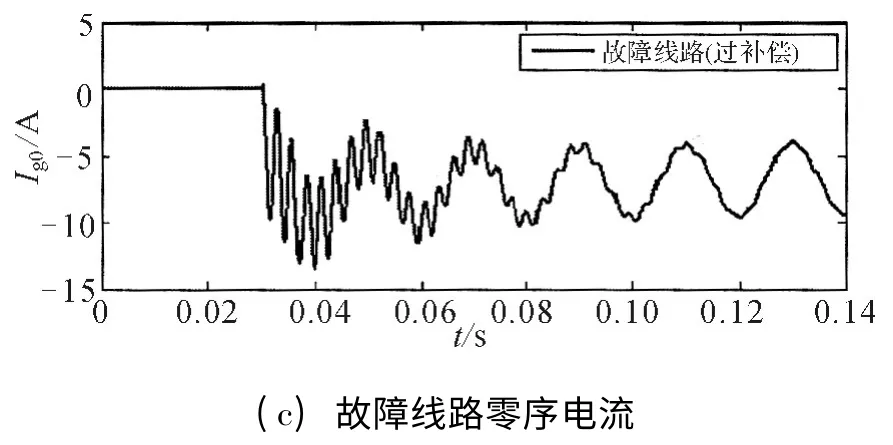
图7 故障初相角为180°时的故障特征量波形

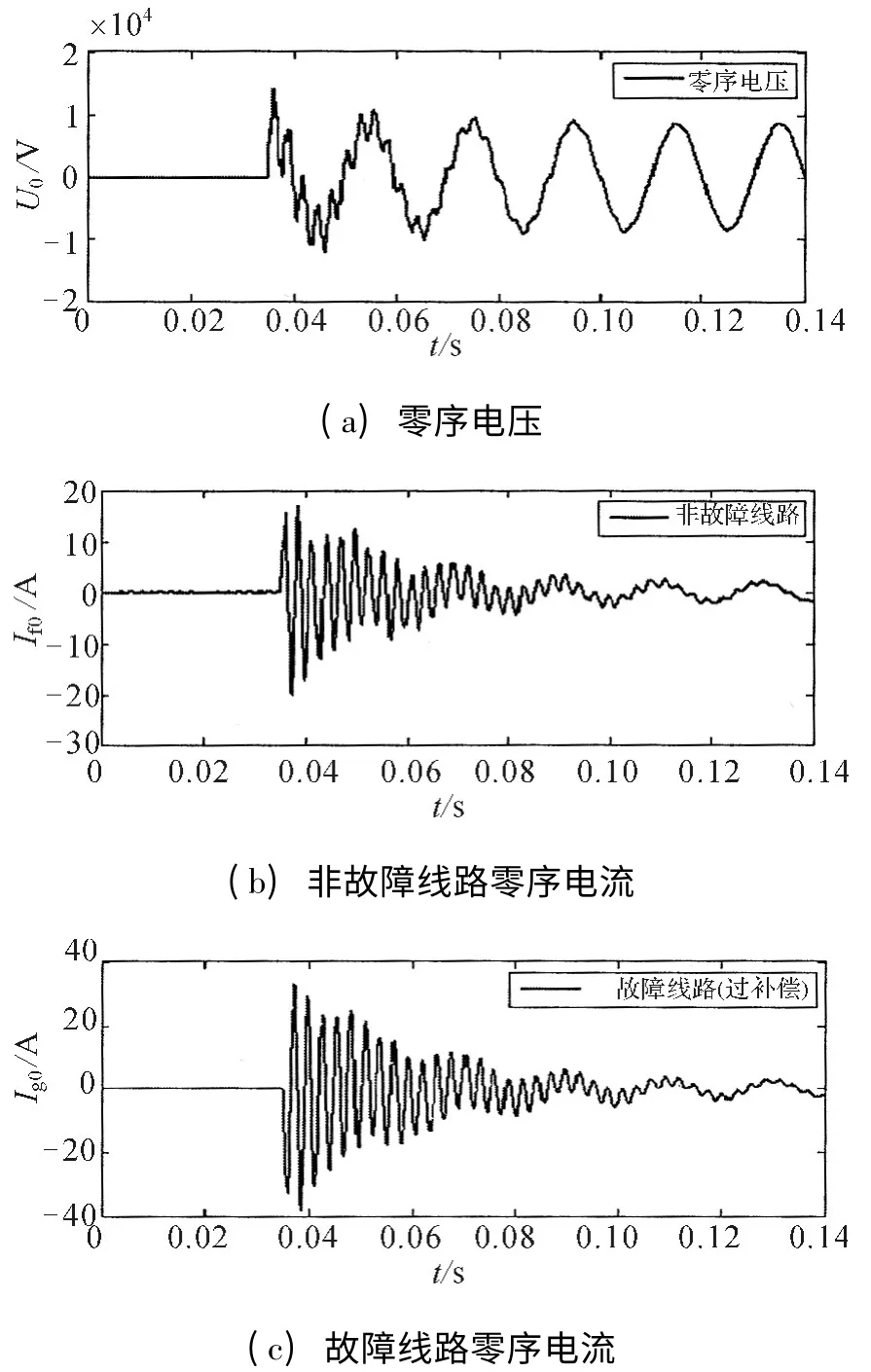
图8 故障初相角为270°时故障特征量波形

由图可知，当故障发生时相电压恰好过零，即φ=180°时，过渡过程中的暂态波动较小，暂态特征量衰减速度较快。当故障发生时相电压处于最大值，即φ=90°或270°时，过渡过程中的暂态波动比较明显，且暂态特征量衰减速度慢。3种情形下，故障线路零序电流暂态峰值都大于非故障线路零序电流暂态峰值;从特征量极性看，故障线路零序电流的故障瞬间极性与零序电压的相反，而非故障线路零序电流的故障瞬间极性与零序电压的相同。

3.3 过渡电阻对故障的影响仿真

保持故障距离和故障时的初相角不变，即L=20 km，φ=65°。分别令过渡电阻Rg=0，50，150，300，500 Ω，对该谐振接地系统单相接地故障进行仿真，根据仿真结果得到不同过渡电阻下的故障量稳态幅值，如表2 所示。限于篇幅，只列出当Rg=50，150，300 Ω 时零序电压和故障线路零序电流波形，以便分析暂态特征量变化趋势，如图9，10，11 所示。

表2 不同过渡电阻下的故障量稳态幅值

图9 过渡电阻为50 Ω 时的故障特征量波形

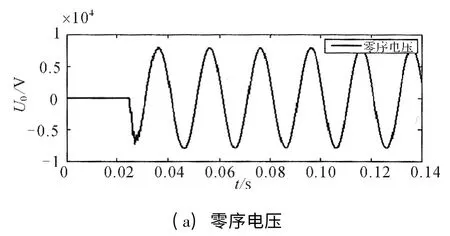
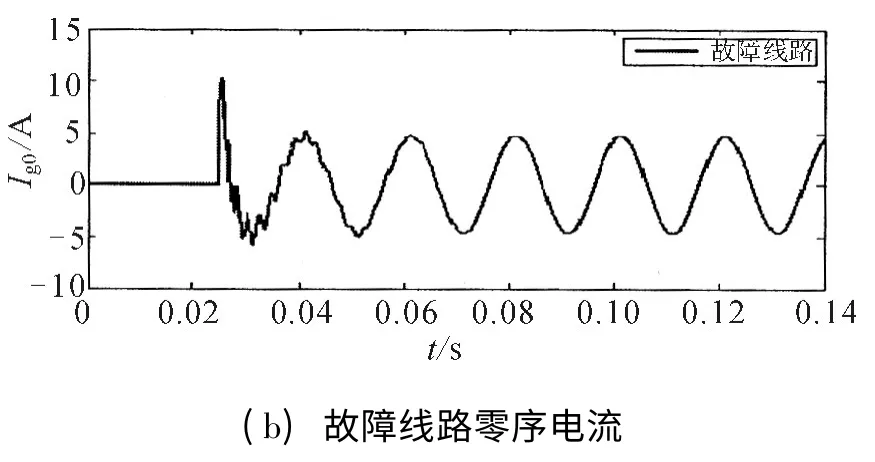
图10 过渡电阻为150 Ω 时的故障特征量波形

图11 过渡电阻为300 Ω 时的故障特征量波形

由表2 中数据可知，随着过渡电阻的增大，接地电流在过渡电阻上产生的压降越来越大，故障相残余电压明显升高，零序电压和各线路零序电流的幅值逐渐减小。

各条馈线零序电流的幅值主要由电容电流的幅值所决定，其幅值受过渡电阻的影响。各线路零序电流的幅值与过渡电阻的变化相反，即过渡电阻越大，零序电流的幅值越小。

由图可知，过渡电阻的大小对暂态过程的影响较大，随着过渡电阻的增大，故障量的暂态冲击值在不断减小，同时暂态过程的衰减越来越快，暂态特征也越来越难以捕捉。

4 结论

本文通过搭建仿真模型，对比分析了不同故障距离、不同故障初相角以及不同过渡电阻对谐振接地系统单相接地故障的影响。仿真结果表明，故障特征量随故障距离的变化不明显，受故障距离影响较小;对于不同的故障初相角，故障线路零序电流暂态峰值都大于非故障线路零序电流暂态峰值，且故障线路零序电流暂态峰值的极性随故障初相角变化，与零序电压的极性相反;随着过渡电阻的增大，零序电流的幅值和故障量的暂态冲击值都在不断减小，同时暂态过程的衰减越来越快。在实际现场的工作中，运行人员可结合特征量的变化规律尽快找到故障点，及时排除故障，减小损失。

本文仿真主要考虑了理想情况下单方面因素的影响，在实际系统中进行检测时，还要综合考虑系统的具体情况，如系统的出线结构、消弧线圈的补偿度及其运行模式等。可在本文研究的基础上，结合实际系统的具体情况，继续进行深入研究。

［1］庞清乐．小电流接地故障选线与定位技术［M］．北京:电子工业出版社，2010．

［2］李磊．谐振接地系统故障选线技术的研究［D］．保定:华北电力大学，2012．

［3］杨淑英，袁宝．基于反向行波的小电流接地系统故障定位［J］．电力科学与工程，2011，27(6):28-32．

［4］任建文，丁浩，李莎，等．基于负序电流的配电网单相接地故障选线方法的研究［J］．华北电力大学学报，2013，40(1):24-29．

［5］窦新宇，李春明．小电流接地系统行波测距方法研究［J］．电力科学与工程，2010，26(2):51-55．

［6］李斌，束洪春．基于瞬时零序功率的谐振接地系统单相接地选线新方法［J］．电力自动化设备，2013，33(4):65-71．

［7］张慧芬，潘贞存，张帆．一种配电网单相接地故障综合选线方法［J］．高电压技术，2008，34(4):788-793．

［8］窦新宇，李春明．基于小波变换的小电流接地故障选线仿真研究［J］．电力科学与工程，2011，27(2):41-43．

［9］陈少华，桂存兵，雷宇，等．基于小波包的永久性单相接地故障的故障选线的仿真研究［J］．继电器，2007，35(1)18-20．

［10］张丽萍，张海，林海峰，等．谐振接地系统全补偿下单相故障的特征分析［J］．电力科学与工程，2009，24(10):9-12．

［11］于群，曹娜．Matlab/Simulink 电力系统建模与仿真［M］．北京:机械工业出版社，2011．

［12］徐波，蔡旭．改进的消弧线圈故障期间调谐方法［J］．电网技术，2014，38(1):107-112．

［13］陈雪洁，付周兴，赵建文，等．瞬时正序网络特性的分析［J］．电力建设，2011，32(10):31-33．

［14］李辉，唐轶，孙常青．谐振接地系统单相接地故障仿真分析［J］．工矿自动化，2012，(1):47-51．