含放射性约束条件的配电网重构研究

韩子骞，刘建华，黄耀东

(长沙理工大学 电气与信息工程学院，湖南 长沙411101)

0 引言

现代化的配电网必须具备满足用电需求、电能质量可靠、省地环保、运行管理高效和技术经济可持续发展的5 项要求。配电网重构问题可以看作为一个开关组合规划问题，其主要目的就是通过可靠高效的开关操作找到一个网损最小，电压最稳定的放射状拓扑结构，主要原因有两点:一是该结构便于配电网的协调和保护;二是减少配电网中的短路电流。因此放射状的配电网运行约束条件几乎存在于所有配电网的重构和扩建问题中，而对于含DG 的配电网重构问题中，该约束条件同样具有举足轻重的地位。于是此问题可以转换为一个混合整数非线性规划问题。其中，网络放射性约束这一关键问题是复杂的并且有待研究。

1 拓扑结构放射性约束

配电网网重构问题的控制变量是开关状态，一般用0～1 两态值进行表示，即重构问题为0～1整数规划问题。对于0～1 整数规划，目前相对有效的求解方法是基于各种随机优化技术，如基于遗传算法［4～6］、免疫算法［7～9］、粒子群算法［10～11］、基于多种方法的混合法［12］等。在配网重构中，网络放射性约束是一关键约束，如何使其快速得到满足是提高计算效率的关键问题之一。

在许多已有的研究成果中，对于放射网的约束条件仅仅是满足公式(1)即可:

式中:m 代表支路数;nb代表节点数。

文献［1，4，5，6］分别用4 种不同的启发式算法来解决配网重构问题，计算过程开始于一个环网结构，随着计算每一步的进行，一些支路被打开，最后形成一种放射状拓扑结构。因此放射结构的条件约束存在于每个启发式算法中，利用公式(1)作为终止条件并不能很好地保证算法的可行性。文献［1］利用公式(1)来作为放射拓扑结构的约束条件，但是这仅仅是一个必要条件而非充分条件。文献［7］提出了一种分支交换算法来解决重构问题，该算法开始于一个可行的放射拓扑结构，然后通过实施一个分支只交换一次来保证新的拓扑结构的放射状。

文献［8］用改进算法来解决配网重构问题，该算法中利用图论的方式来实现放射拓扑结构;文献［12］用二次协作方法来解决问题，该文将放射的约束条件隐含在遗传算子内。在文献［3］中研究含有分布式电源的配电网重构问题，上文提到的满足公式(1)即可保证放射性的约束条件已完全不适用于该模型，而是要根据具体问题提出更多的约束条件，此项工作还是相对复杂的。文献［11］将不在任何环路上的开关都删除，将开断效果一致的支路合并为一个支路组而得到简化网络，并在简化过程中运用每个支路组中最多只有一个开关开断的规则。这种方法改进了一个支路组中开断两个及以上开关无效解的产生，因而大大提高了优化网络结构产生的几率。文献［13］研究配电网重构优化模型及优化方法，结合网络层次结构特征进行拓扑识别，并利用层次的前推回代方法进行潮流计算，采用广泛学习量子进化算法进行优化重构，然后再考虑DG 接入的情况。文献［12］首先生成一个连通性判断程序来判断每一个染色体对应的网络结构图是否满足放射状的约束条件(即网络结构中不存在“环网”和“孤岛”现象)。如果判断出该染色体对应的网络结构图不连通，说明它是不满足放射条件的，于是采用基因疗法的“补”操作和“泻”操作将其改变成可行解，这样既满足了放射约束条件，也避免了算法陷入局部最优解的问题，又提高了算法的运算效率。这些论文都意识到了网络放射结构的重要性，但是却没有提出详细分析方法及约束条件。

1.1 拓扑结构特点

从上述的文献可以很清楚地看出，拓扑结构的放射性约束作为一个问题还有待研究，本文提出一种新的约束方法来确保配电网放射运行，如果此假设成立，那么该约束条件可以用于解决传统配电网重构和含DG 的配电网重构的0～1 整数规划问题。观点如下:配电网络的拓扑结构可以看作是一幅有m 个节点和n 条支路的连通图，从图理论的角度来看，他可以看作为一棵没有环网的树，因此可以把“这棵树”比作配电网络的拓扑结构，这棵树是由(m-1)条树枝相连的子树构成的。因此一个由nb个节点构成的放射状拓扑结构需要满足如下两个条件:

条件1:该拓扑结构必须有(nb- 1)条支路;

条件2:该拓扑结构必须是连通的。

配电网拓扑结构的形成必须同时满足条件1和条件2，仅仅满足条件1 不能保证拓扑结构的可靠性。一个满足上述拓扑结构的主要特点如下:

(1)系统中只存在一个根节点;

(2)其他所有节点都为负荷节点;

(3)必须满足基尔霍夫第一定律;

(4)找到最优的拓扑结构。

1.2 一般配电网络放射性约束条件

用一个五节点的配电网拓扑结构来简单论证，该网络中有一个根节点和4 个负荷节点，其主要目的是在满足放射拓扑结构的条件下尽量减少有功功率损耗。如图1 所示，在该问题中只需要满足基尔霍夫第一定律即可，所以不必特殊指出支路的电阻和电抗，其数学模型需要满足以下条件:

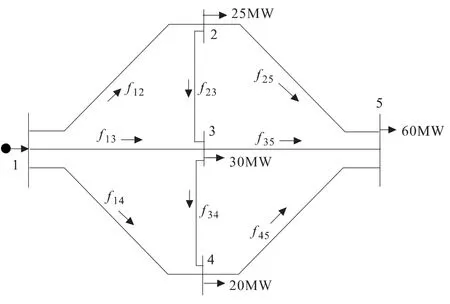
图1 五节点拓扑结构

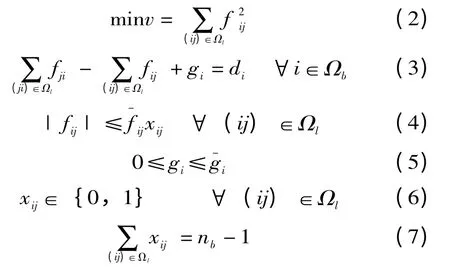
式中:Ωl，Ωb分别代表支路集和节点集;nb表示节点数;v表示总的功率损失;f表示总的投资和运行成本。

在这里面xij是一个二进制变量，它代表开关状态，当xij=1 时表示开关闭合，当xij=0 时表示开关闭合。节点i 和节点j 之间的有功功率损失表示为fij，其中变量gi为变电站i 提供的有功功率，参数di代表节点i 的有功功率需求，变量代表分支ij 的最大有功潮流。参数表示变电站i 的最大有功功率极限。本文对上述算法采用Matlab编程计算，假设，，经过计算可以得到如下结果:

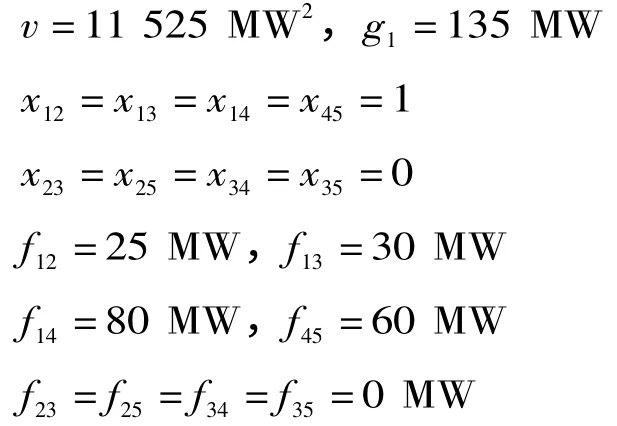
1.3 含DG 配电网络放射性约束条件

在更加普遍的配电网络中，上文中的条件1必须改成:

式中:nbs代表总的变电站节点数。如今，DG 的引入越来越多的出现在配电网重构的问题中，因为无功电源都包含在负荷节点中，所以公式(1)～(4)仍然满足，当DG 独立的向某部分负荷供电的时候，即所谓的孤岛运行。但是约束条件2 不能确保公式(3)达到功率平衡，所以需要补充新的约束条件(9)～(12)，以确保分布式电源不孤立于整个网络。

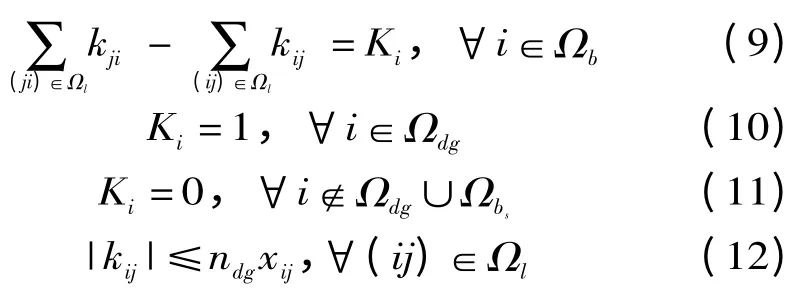
式中:Ki代表由变电站提供的每个分布式电源的假想负荷;变量kij表示支路ij 的假想潮流;Ωdg表示分布式电源节点集;ndg表示分布式电源的节点数量;Ωbs表示总线变电站节点集。

2 放射约束条件在配电网重构中的应用

网络重构的数学模型:

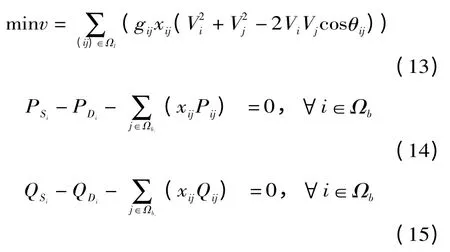
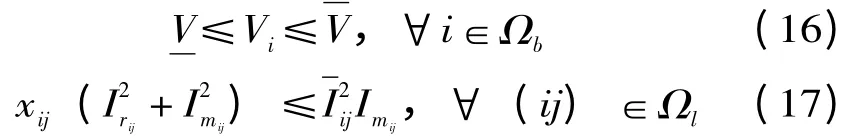
式中:Vi表示节点i 的电压大小;，分别表示最小电压幅值和最大电压幅值;为支路ij允许流过的最大电流;，分别为流过支路ij 的实际电流和假设电流，

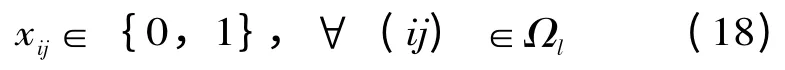
式中:xij代表重构支路，公式(18)为变量xij的二进制表示。如果支路ij 之间的开关闭合则用1表示，反之，表示为0。

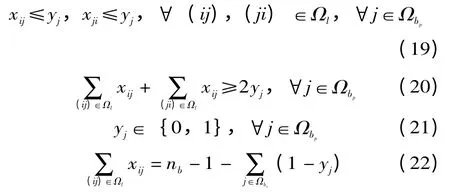
在较优的重构模型中，网络中仅有一个根节点并且存在转移节点，这种特殊的网络结构可用公式(22)来表示，含有传输节点的网络模型可用公式(19)～(22)来约束。Pij，Qij分别为节点i 流向节点j 的有功功率和无功功率，由下式得出:

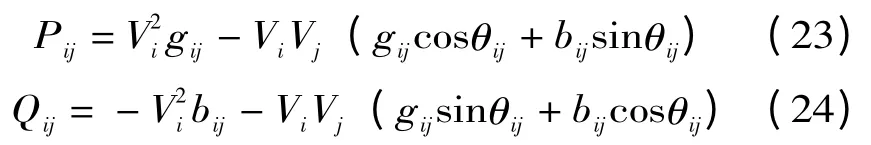
式中:gij，bij为支路ij 的电导和电纳。公式(17)中的Irij，可由下式得出:

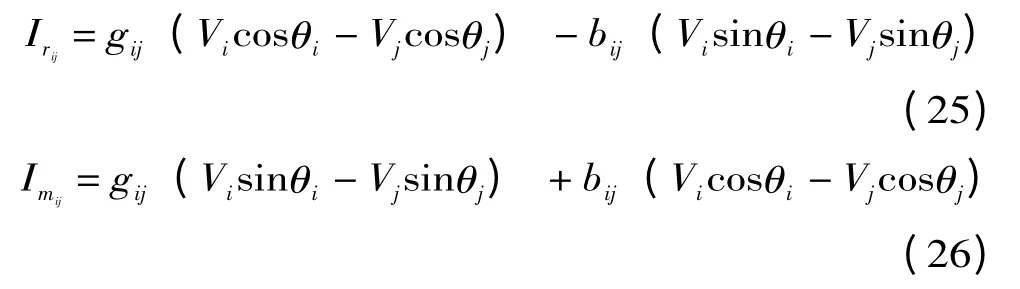
上述问题是一个非线性有约束整数混合优化问题，本文把前文放射性约束的数学模型用于基于改进粒子群随机算法中，该算法求解配网重构问题的算法流程图在诸多文献中已有详细介绍［10］，本文不在赘述。

3 算例分析

本文对上述算法采用Matlab 编程，并且与其他文献进行比较，来验证该算法的有效性，电脑配置:Windows7 操作系统，CORE i5 CPU 3．10GHZ，4GB 内存。

(1)算例1:以IEEE33 节点系统来验证本文的可行性，配电网有33 个节点，37 条支路，其中的5 条为联络开关，额定电压为12．66 kV。用提出的放射约束条件以网损最小为目标函数进行重构计算最终的拓扑结构图如图2 所示，其中节点5，14，20 都为连通的，而节点31 不连通，节点31 重构后成为了终端节点，本次测试总的线路损耗为107．79 kW。与文献［13］相比，有功网损明显降低。

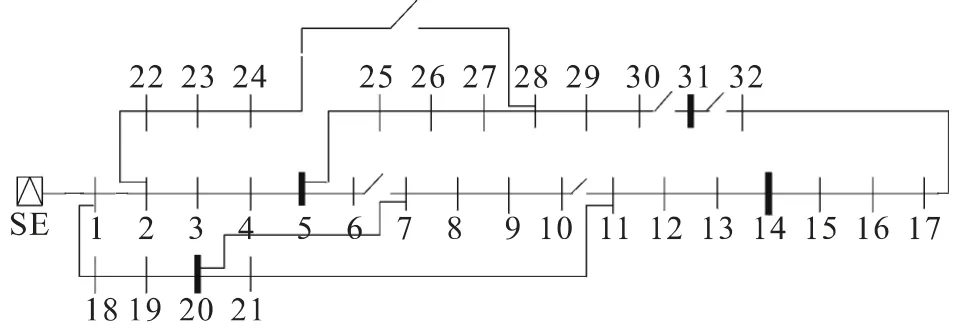
图2 IEEE33 节点重构后结构

(2)算例2:选择IEEE69［51］节点测试系统来求解配电网重构问题，网络包含69 个节点，73条支路，其中包含5 条联络支路，总负荷为3 802+j3 694 kVA，假设在节点25 接入一台P=200 kW 的DG，如图3 所示，用上述算法来进行重构。

(3)结果分析

基于放射性约束的算法重构结果如表1 所示，网络初始结构的网损值为225．002 kW，本文通过一系列放射结构的约束条件以及接入DG 的网络优化后，网损值仅有80．99 kW，节省功率为144．012 kW。与文献［2］改进遗传算法相比，可以看出由于DG 的接入使网损降低，相对于文献［8］而言，本文得到优化结果的迭代次数和总的计算时间比文献［8］要少。一方面是由于本文采用的粒子群进化算法相对于文献［8］的微分进化过程简单，每次迭代需要进行的潮流计算次数较少;文献［13］中对分布式电源的容量和接入位置进行了优化配置，在优化结果上有了一定的提高，但是QIEA 的种群是由量子比特组成的一个概率系统，其个体在观测时充满了随机性，以往研究中对量子门更新的引导过程只是利用上代的最优信息来引导，没有充分利用当前最优种群中其他个体的信息，容易陷入局部最优，因此文献［13］将广泛学习思想引入到量子进化算法中，但是这增加了计算的复杂度，使收敛速度有所下降;另一方面，本文提出的放射拓扑结构约束条件可以相对减少每次拓扑检测需要的时间，从而使得总体计算时间相对提高。同时也证明了本文方法比起其他算法具有一定的优越性。

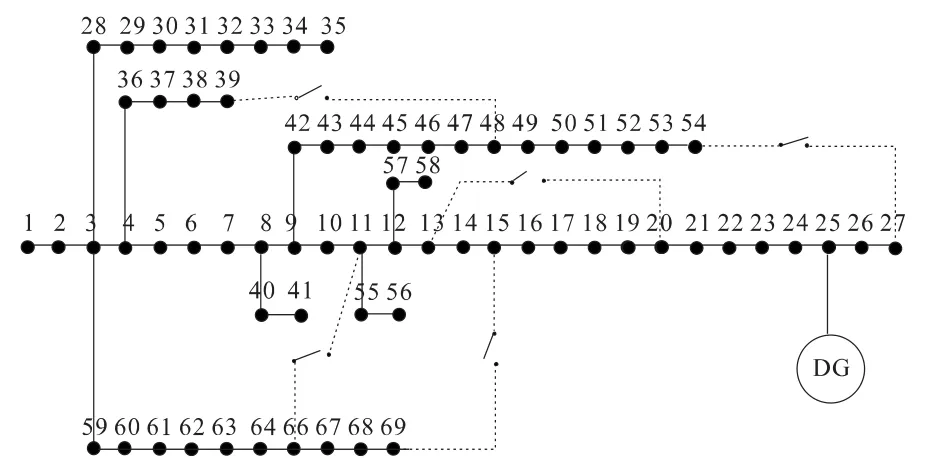
图3 IEEE69 节点测试系统

表1 配电网重构结果

如图4 所示，IEEE69 节点系统在配电网重构之前的所有节点中电压标幺值最低为0．908 08 p．u．，而经过基于放射性约束的重构计算之后，该系统的所有节点中电压标幺值最低为0．943 6 p．u．，可见节点电压值有所改善，经过重构之后，系统整体的电压水平也有所改善了。

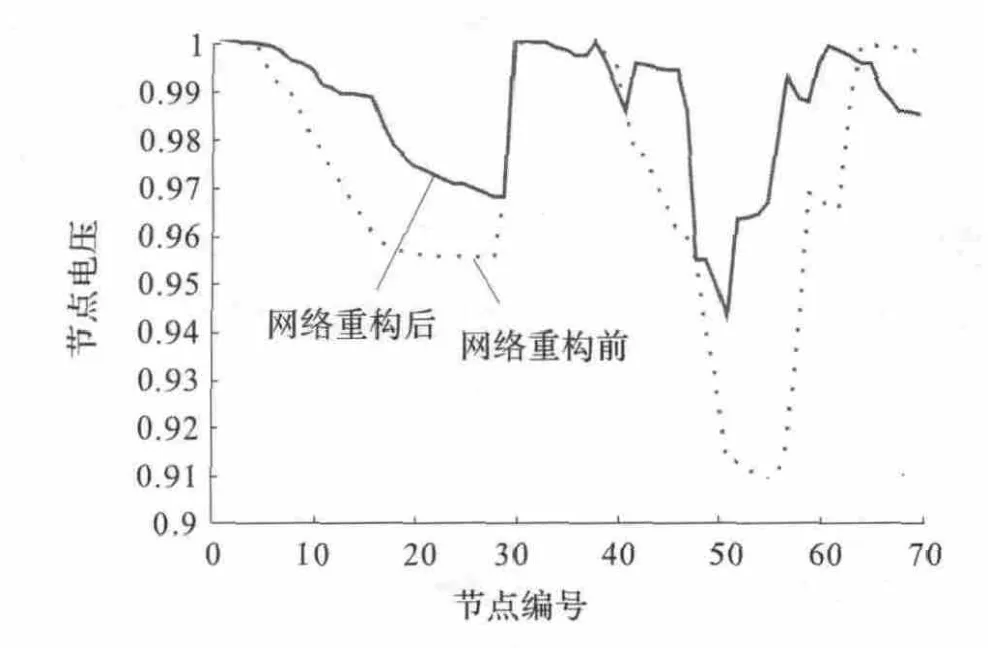
图4 IEEE69 节点系统的配电网重构前后节点电压的标幺值

4 结论

配电网重构作为配电自动化的关键技术之一，越来越受到专家学者的重视。本文根据配电网的结构特点，提出满足放射性约束的充分条件而非必要条件，对配电网进行约束，同时考虑DG 并网对约束条件及网络重构的影响。最后把该约束条件纳入基于粒子群优化方法的配电网重构中，测试结果表明，在该约束条件下，算例能快速地求得全局最优解，证明了本文方法的可行性和优越性。

［1］Schmidt H P，I da N，kagan N，et al．Fast reconfiguration of distribution systems considering loss minimization［J］．IEEE Trans．Power Syst，2005，20(3):1311-1319．

［2］邓桂秀，江修波，蔡金锭．基于混沌二进制粒子群算法的配电网重构研究［J］．电子科学与工程，2013，29(9):34-37．

［3］庄园，贺海，杨晓慧，等．含分布式电源优化调度的配电网重构［J］．电网与清洁能源，2013，28(11):13-18．

［4］麻秀范，张粒子．基于十进制编码的配网重构遗传算法［J］．电工技术学报，2004，19(10):65-69．

［5］Mendoza J，Lopez R，Morales D，et al．Minimal loss reconfiguration using genetic algorithms with restricted population and addressed operators real application［J］．IEEE Trans．on Power Systems，2006，21(2):948-954．

［6］Enacheanu B，Raison B，Caire R．Radial network reconfiguration using genetic algorithm based on the matroid theory［J］．IEEE Trans．on Power System，2008，23(1):186-195．

［7］蒙文川，邱家驹．基于免疫算法的配电网重构［J］．中国电机工程学报，2006，26(17):25-29．

［8］林济铿，王旭东，陈云山，等．基于可行解搜索和自适应免疫算法的配网重构［J］．天津大学学报，2008，41(12):1505-1511．

［9］余建明，张凡．基于改进免疫遗传算法的配电网重构［J］．电网技术，2009，33(19):100-105．

［10］许立雄，吕林，刘俊勇．基于改进粒子群优化算法的配电网络重构［J］．电力系统自动化，2006，30(7):27-30．

［11］李振坤，陈星莺．配电网重构的混合粒子群算法［J］．中国电机工程学报，2008，28(31):35-41．

［12］Wang C ，Cheng H Z．Optimization of network configuration in large distribution systems using plant growth simulation algorithm［J］．IEEE Trans．on Power System，2008，23(1):119-126．

［13］秦艳辉．含分布式发电的配电网重构优化研究［D］．四川:西南交通大学，2012．

［14］史常凯，徐文武，孟晓丽，等．智能配电网条件下的网络重构与供电恢复探讨［J］．电力建设，2012，33(1):12-16．

［15］Khodr H M，Martinez C J，Matos M A，et al．Distribution systems reconfiguration based on OPF using benders decomposition［J］．IEEE Trans on Power Delivery，2009，80(2):562-571．