多分支配电网故障选线方法研究

刘慧琼，孙辉军，匡文凯，3，曾祥君

(1．长沙理工大学 智能电网运行与控制湖南省重点实验室，湖南 长沙410114;2．株洲市电业局，湖南 株洲412000;3．湖南湘能智能电气股份有限公司，湖南 长沙410013)

0 引言

电力系统配电网分布广泛、结构复杂，发生故障的概率较大。其中多分支配电网的故障分支真伪难辨、测距困难，因此，深入研究配电网的故障选线方法尤其重要［1］。

传统的选线方法有拉路法、注入信号法、稳态信号法、暂态分量法、人工选线法［10，11］等，但配电网多为小电流接地系统，零序电流的提取受系统的接地方式及系统正常运行不平衡电流的影响，实际运行中选线效果不理想［2～4］。配电网发生故障后，故障点将会在产生包含丰富故障信息的暂态行波，利用该暂态行波选线具有不受中性点接地方式、过渡电阻、故障时电压等因素影响的优点。因此，将行波理论运用到配电网的选线中将能克服其他方法的诸多不足［5，6］。

本文提出一种基于多端行波信号的故障测距方法。该方法只需在配电网支路末端变压器选择性的安装行波信号采集装置，利用初始行波的到达时间差、线路长度及分支点位置的关系，即可完成选线测距。最后用EMTP 仿真软件验证了该方法的有效性。

1 故障行波在配电网的传播特性

电力系统发生故障时会使故障点的电压/电流发生突变，产生高频的暂态信号，该信号定义为行波。它以一定的速度沿线路向整个配电线路传输。当遇到波阻抗不连续点时，会发生折返射现象。配电网具有分支多的特点，对于带分支的故障线路，除故障点、波阻抗不连续点还包括母线、线路终端及分支的节点等［8，9］。

1.1 故障行波在分支路上的传输特点

配电网主要为树形辐射，从图论的角度，配电网可以用图1 所示的无向量图来表示［7］。图中M表示母线端，A表示末端变压器，a，b表示线路节点。

若a，b 点间F 处发生故障时，将会产生向两端传播的故障行波，以F 为分界在各自范围内传播。故障行波在传输过程中，遇上波阻抗点A，a将会发生折返射，有以下几个特殊行波路径:直接由a 点产生折射，达到母线M 端，SM1:F→a→M;在M 点发生反射达到a 点，并由a 点再次反射回M 端，SM2:F→a→M→a→M;故障行波从F点通过B 点折射传输至A 点，SA1:F→M→A;在A 点发生发射传输至B 点，再由B 点反射回A点，SA2:F→a→A→a→A，等。行波在发生折返射时，将会根据反射系数与折射系数发生不同程度的衰减，在信号衰减至零以前，行波信号将持续在线路中传输。若以A 点与M 点作为获取行波信号的参考点，将F→a→M，F→a→A 这类传输至参考点距离最短的路径，称为初始行波传输最短路径。

图1 行波传输路径图

1.2 故障行波在分支线路上的衰减

已有的行波选线技术，通过在母线M 端安装行波定位装置获取故障行波信号，利用故障线路与非故障线路的行波极性相反或行波幅值远大于非故障线路的特性来进行故障选线。当故障F 发生在配电网多分支的支路上时，故障行波需经过多次折返射后才能达到母线端，其故障分量信号将会大幅减弱，影响行波信号的检测，如果无法检测到有效行波信号，则导致故障选线失败。

如图2 所示，支路L 发生故障时，将产生电压入射波u't与电流入射波i't，其在支路L1，L2上折射波可用彼德逊等值法则计算，得

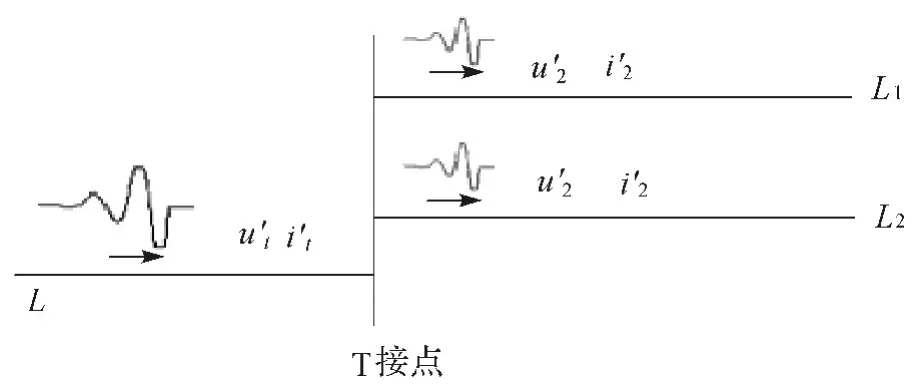
图2 行波信号在T 接点的折反射

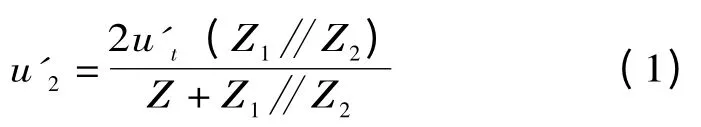
式中:Z，Z1，Z2分别为支路L，L1，L2的波阻抗，假设其线路结构相同，则其波阻抗均为Z，则电压反射波为

电流反射波为:

即L1，L2上的电流行波为入射波的1/3，信号衰减非常严重，在多分支线路上发生故障时，故障行波到达母线端时，有可能导致行波信号无法采集。要想彻底解决这个问题，必须确保能准确采集到行波信号。

2 多分支线路的故障选线原理

基于故障行波在多分支配电网线路上的传输特性，在有关输/配电网行波技术分析中，将变压器的波阻抗看作远线路的波阻抗。实际上，在冲击电压作用下，变压器不能再看作集中参数，要考虑绕组的电感、绕组对地电容和纵向电容的影响，看成具有分布参数的电路，即变压器可用归算至首端的对地电容来代替，通常称为入口电容。因此，可选择性的在配电网分支的配电变压器外壳接地线上安装行波检测装置来获取行波信号。如果故障支路或附近支路发生故障，则该装置即可检测到行波信号。在带多分支线路中选定几个点安装行波信号检测装置，将检测装置两两组合构成双端定位系统，通过检测初试行波的到达时间并结合D 型行波测距原理，融合各组的选线结果，完成配电网的故障选线。

2.1 D 型行波故障测距原理

D 型行波故障测距原理:利用故障暂态行波的双端测距原理，根据初始行波达到线路两端测量点的绝对时间之差值计算故障点到两端测量点之间的距离［1］。假设M，N 点为两端测量点，其公式为:

式中:LMF为M 端到故障点的距离;v表示行波传输的速度;tM与tN分别表示初始行波到达M，N点的时间;l 为线路MN 的最短传输路径长度。

2.2 故障分支的判定原理

根据故障行波在配电网多分支路径上的传输特点可知:在两端测量点检测到的故障信号除了由最短路径MN 之间的故障点产生外，还可能从MN 间的某个分支故障点产生。

电网中各分支及支路的长度为已知量，结合D 型故障测距法与式(4)分析可得判别式为:

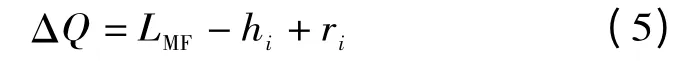
式中:hi表示最短路径上第i 个分支点与测量端点间的距离;i 为变量;ri为合理的裕度。

若ΔQ≠0，表示故障定位成功，故障点位于行波最短路径MN 之间。根据ΔQ 可确定故障分支，由LMF可确定故障分支及故障点。

若ΔQ=0，则故障点位于最短路径MN 点之外的分支上，即为i 所代表的分支。

3 多分支配电网的故障选线

对于复杂分支的配电网，若要实现全网的故障选线，则需在配电网各分支末端均安装行波采集装置。该方式经济成本过高不适合实际工程应用。因此，本文提出了一种行波检测装置的优化配置方法，选择性的在配电网分支的配电变压器上安装行波采集装置，减少经济成本。

3.1 行波采集装置的优化配置

图3表示一个复杂分支的配电网无向量拓扑图，图中a，b，c，d表示分支节点，A，B，C，D，E，F，G，H，I，J 点分别为配电变压器端口。以该图为例，优化配置方法如下:

(1)在线路首末两端配电变压器安装行波采集装置(如图3 的A，F 点)。

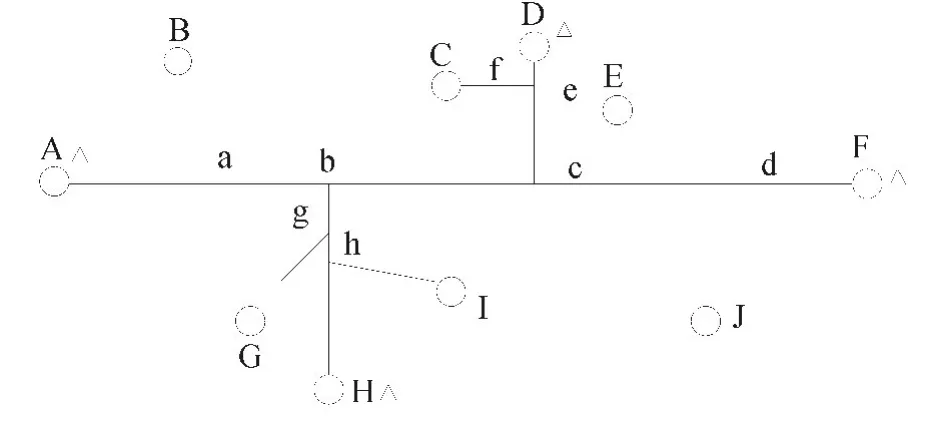
图3 配电网无向量拓扑图

(2)以首末两端为基点，分析其最短路径上的分支节点，可分为单一分支节点与多分支节点(即分支上还有分支的节点)。对其单一节点(如图3 中a，b)无需安装行波检测装置，选取多分支节点进行下一步分析。

(3)对于多分支节点(如图中a，c)，选取该节点为线路首端在其对应的线路末端安装变压器(如图中的H，D)。对于分支线路上结点按(2)中的方法进行继续分析。

3.2 基于D 型原理的故障选线方法

记录行波装置采集的行波信号，采集各初始行波到达的时刻。将行波检测装置进行两两组合，构成多组D 型行波选线系统。根据2．2 可分析:

情况(1)时，即有任意D 型系统能成功定位时，则直接确定故障分支。

情况(2)时，当任意组均不能成功定位时，则需要将各个系统的选线结果融合，通过进一步分析最终确定故障定位。

当双端定位系统将故障点定位在某一个支路节点，如节点为单一节点，该节点的分支所对应的分支为疑似故障线路。如是多分支节点，则排除该定位系统所包含的主线路及单一支点的线路为故障线路的可能性，确定疑似故障区域。最后将多组系统的结果融合，排除非故障线路，取疑似故障线路的交集，最终完成故障选线。

3.3 配电网分布式行波信号定位流程

基于上述以双端定位法为基础，融合多组定位系统结果进行故障选线，选线流程图如图4所示。

(1)分析配电网的分支情况，根据行波采集装置的优化配置原则，选择性的在有需要的分支点末端变压器上安装行波采集装置。

(2)根据装置采集的行波信号，提取初始行波波头的到达时间

(3)对于初始行波波头到达时间进行两两组合，构成多组选线系统，采用双端行波法进行故障定位。

(4)判断是否能精确定位，若能实现精确定位，则输出最终结果，否则继续进行分析。

图4 选线流程图

(5)根据故障选线确定的故障节点，排除非故障线路，选出疑似故障区段。

(6)将多组双端定位系统的故障选线结果融合，取故障区段的交集，最终确定故障分支，输出定位结果。

4 算例验证

本文采用EMTP 对某复杂配电网系统进行了仿真分析。仿真模型如图5，该模型采用了分布式参数模型，同时考虑了线路对地电容的影响。该仿真线路中，电缆线路已归算为架空线路的长度，因此，行波传输的速度按2．98 ×108m/s 计算。根据仿真参数的具体设置情况，设置仿真裕度ri为±0．02 km。

设置故障点为Ee 线路中点，即距离E 端1．5 km 处。根据优化配置原则，选取A，D，H，F4个端点安装行波采集装置，获取故障行波信号，进行故障选线分析。根据仿真结果，在各端点获取的原始波形如图6～9 所示。

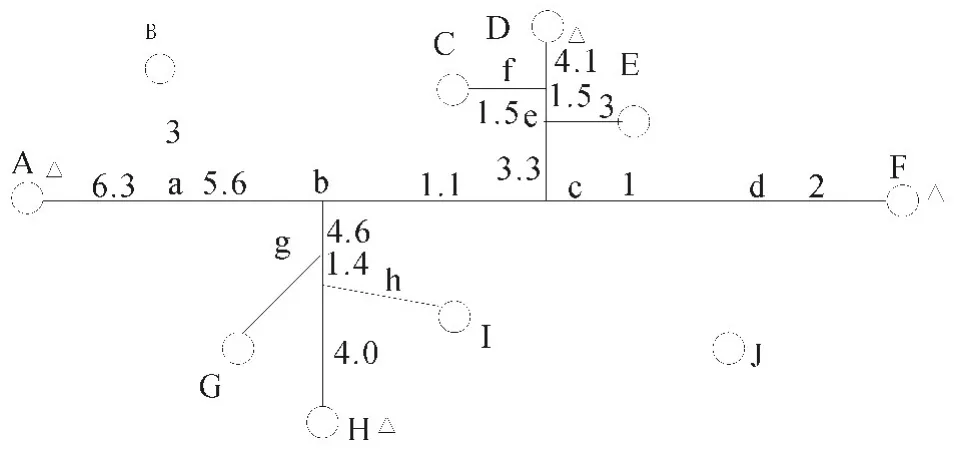
图5 仿真模型图

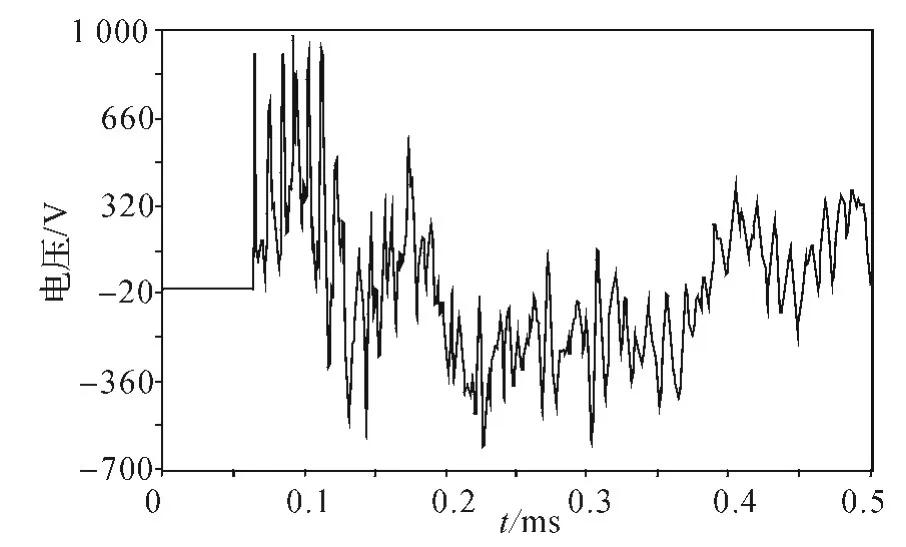
图6 A 处测取的原始电压行波

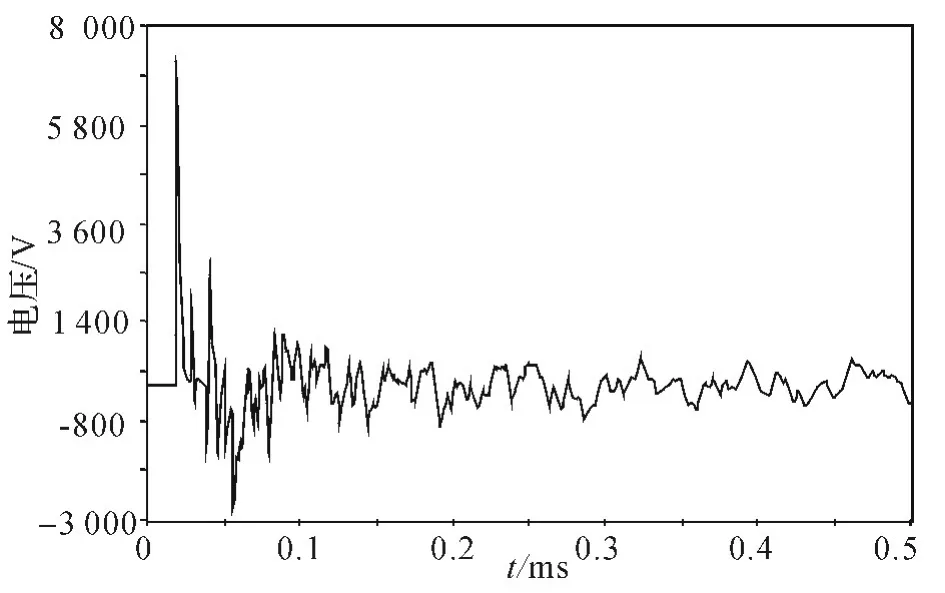
图7 D 处测取的原始电压行波图

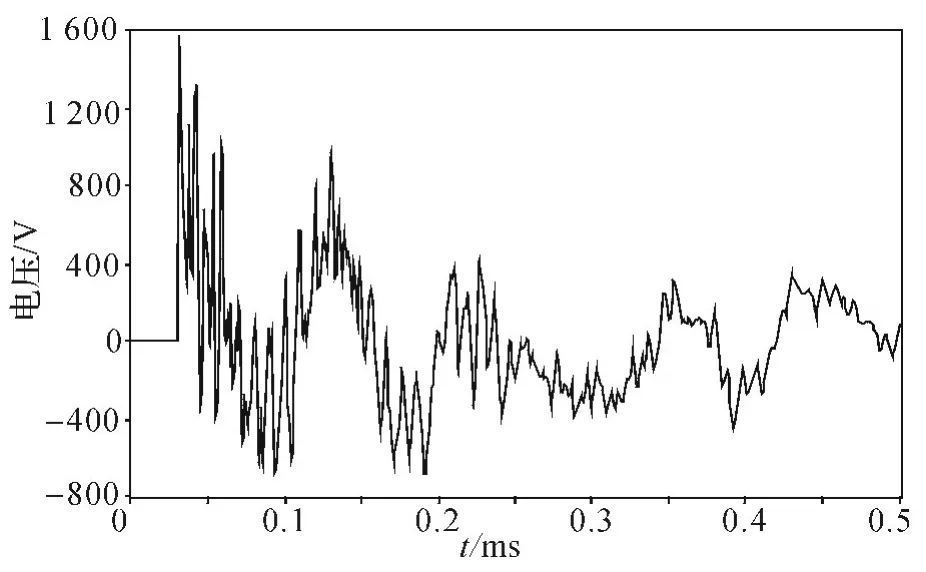
图8 H 处测取的原始电压行波图

根据各端点采集的原始波形，采集的初始行波波头达到时间如表1 所示。

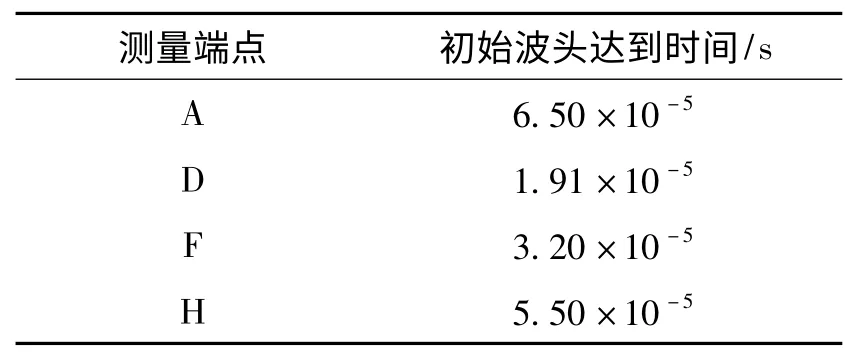
表1 测量点行波达到时间

图9 F 处测取的原始电压行波图

将4 个测量端点的初始行波波头达到时间两两组合，组成6 组D 型定位系统，各系统的最短传输路径如表2 所示。

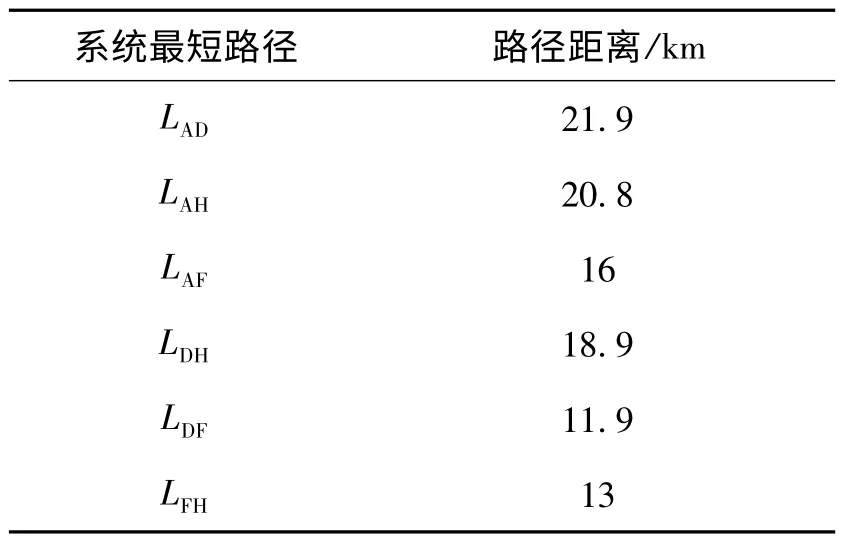
表2 D 型定位系统的最短路径距离

根据以上数据，对配电网进行故障选线分析:

(1)根据双端定位公式选取A，D 点配合组成双端定位系统，以A 点时间为基准，计算故障距离A 点为17．789 km，可判断应位于节点f 处，排除非故障线路后，可判定故障分支为Ee。

(2)根据双端定位公式选取A，H 点配合组成双端定位系统，以A 点时间为基准，计算故障距离A 点为11．89 km，可判断应位于节点b 处，排除非故障线路后，可确定故障区段为线路Fb 及其所包含的分支。

(3)根据双端定位公式选取点A，F 点配合组成双端定位系统，以A 点时间为基准，计算故障距离A 点为12．917 km，可判断应位于节点c处，排除非故障线路后，可确定故障区段为线路Dc 及其所包含的分支。

(4)根据双端定位公式选取D，H 点配合组成双端定位系统，以H 点时间为基准，计算故障距离H 点为14．799 km，可判断应位于节点e 处，排除非故障线路后，可判定故障分支为Ee。

(5)根据双端定位公式选取D，F 点配合组成双端定位系统，以H 点时间为基准，计算故障距离F 点为7．83 km，可判断应位于节点e 处，排除非故障线路后，可判定故障分支为Ee。

(6)根据双端定位公式选取H，F 点为参照点，以H 点时间为基准，计算故障距离F 点为4．098 km，可判断应位于节点c 处，排除非故障线路后，可判定故障区段为线路Dc 及其所包含的分支。

融合以上6 组D 型定位系统的选线结果，最终确定故障线路为Ee，与参数预设结果相符，能准确选出故障线路。

5 结论

本文提出的配电网选线方法，按照行波采集装置优化配置原则选择性的在配电网末端安装行波采集装置，利用采集到的初试行波达到时间进行故障选线，不需要使用行波信号的其他特征量，不受网络参数变化带来的影响，经过仿真验证，该方法选线结果准确。

［1］葛耀中．新型继电保护与故障测距原理与技术［M］．西安:西安交通大学出版社，2007．

［2］肖白，束洪春，高峰．小电流接地系统单相接地故障选线方法综述［J］．继电器，2001，29(4):16-20．

［3］黄芳，陈志军，蒋晓宇．小电流接地系统故障选线算法综述［J］．江苏电机工程，2005，24(3):80-84．

［4］李冬辉，史临潼．非直接接地系统单相接地故障选线方法综述［J］．继电器，2004，32(18):74-78．

［5］董新洲，毕见广．配电线路暂态行波分析和接地选线研究［J］．中国电机工程学报，2005，25(4):1-5．

［6］王阳，曾祥君，黎锐烽，等．基于图论的配电网故障定位新算法［J］．电力系统自动化，2012，36(8):143-147．

［7］邓丰，陈楠，曾祥君，等．基于图论的电网故障行波定位装置最优配置算法［J］．电力系统自动化，2010，34(11):87-92．

［8］曾祥君，尹项根，林福昌，等．输电线路故障GPS 行波定位装置实验测试研究［J］．中国电机工程学报，2002，22(6):42-46．

［9］哈恒旭，张保会，吕志来．高压输电线路单端测距新原理探讨［J］．中国电机工程学报，2003，23(2):42-45．

［10］严凤，杨奇逊，齐郑，等．基于行波理论的配电网故障定位方法的研究［J］．中国电机工程学报，2004，24(9):37-43．

［11］张帆，潘贞存，张慧芬，等．树型配电网单相接地故障行波测距新算法［J］．中国电机工程学报，2007，27(28):46-52．