等谱AKNS方程的约化

（海军航空工程学院基础部，山东烟台264001）

寻求非线性偏微分方程的精确解，一直是孤子理论研究中的重要内容之一。目前，已经有许多成功的方法，如反散射变换方法[1]、Dabux变换方法[2]、Hirota[3]方法、Wronskian[4-7]技巧等等，其中，Wronskian 技巧有明显的优越性，Wronskian 行列式每一列是其前一列的导数，因而这种类型的行列式的高阶导数只是少数几个同阶行列式的和构成，使得由此表达的解能直接代入方程验证。孤子方程的双Wronskian 解是对单Wronskian解的推广，本文推广双Wronskian行列式元素满足的条件，通过等谱AKNS 方程的约化，得出非线性Schrodinger 和mKdV 方程的新双Wronskian 解，包括有理解。

AKNS 方程是非常重要的非线性发展方程，二阶和三阶等谱的AKNS方程组分别为：

令r=q∗（∗为共轭复数），且以-it代替t时(i2=-1)，方程（1）约化为等谱的非线性Schrodinger 方程：

类似的，令q=r=v，方程（2）约化为等谱的mKdV方程：

本文组织如下：第1 部分通过约化分别得到非线性Schrodinger和mKdV方程的新双Wronskian解；第2部分，给出2个方程的双Wronskian 形式的有理解；第3部分给出结论。

1 非线性Schrodinger 和mKdV 方程的新双Wronskian解

在方程（1）中若施以分式变换：

则g、f、h 满足双线性方程：

类似的，在方程（2）中施以分式变换（5），则得到其双线性方程：

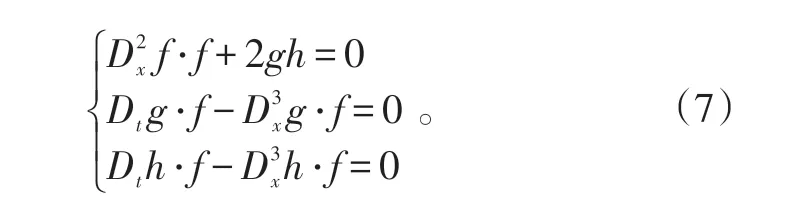
式（7）中，D是著名的Hirota算子[3]，定义如下：

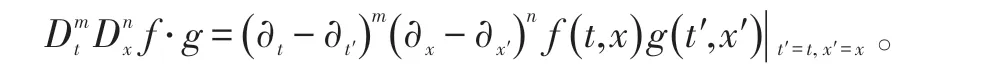
为得到方程（3）新的双Wronskian解，引入记号[6]：

式中，φ、ψ是2个N+M 维的列向量。

运用Wronskian技巧，可以证明下面2个引理：

引理1[8]：二阶AKNS方程（1）的双线性方程（6）有下列双Wronskian行列式解：

式（8）中，φ、ψ 满足条件：

A是一个(N+M+2)×(N+M+2)的独立于t 和x任意实矩阵。

引理2[9]：三阶AKNS方程（2）的双线性方程（7）有双Wronskian行列式解（8），φ、ψ 满足下列条件：

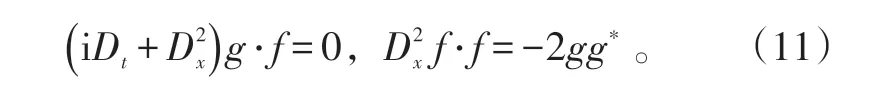
由引理1可以推出方程（11）的新双Wronskian解。定义矩阵：

式（12）中：

设

由行列式性质，可以知道f=f∗，

定理1：等谱的非线性Schrodinger方程（3）的双线性方程（6）有如下新双Wronskian解：

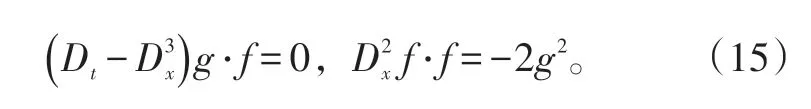
与二阶AKNS方程类似，

式（16）中：

定理2：等谱的非线性mKdV方程（4）的双线性方程（15）有如下新双Wronskian解：

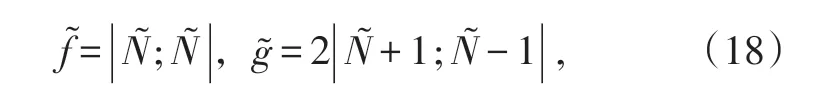
2 非线性Schrodinger和mKdV方程的有理解

从式（9）中可得到：

其中，C、D为N+M+2 维常数列向量。如果矩阵

则AN+M+2=0，这时式（19）可被截断为

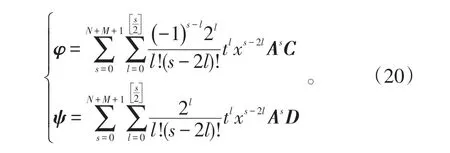
相应的，

式中，j=1,2,…,N+M+2。

令c1=d1=1，ck=dk=0()

k=2,3,…,N+M+2，有

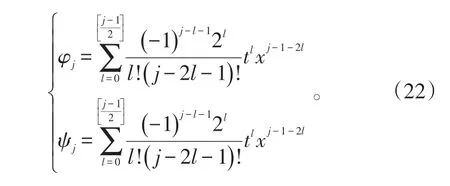
当以-it代替t时，从式（22）可以看出：

从而推知f∗=f，g∗=h，即r=q∗，这样可得到定理3。

定理3：等谱非线性Schrodinger 方程（3）有双Wronskian形式的有理解：

其中，φj、ψj满足条件（22）。

类似的，从式（10）中可得到

式中，C′、D′为N+M+2 维常数列向量。

如果矩阵

则AN+M+2=0，这时式（23）可被截断为：

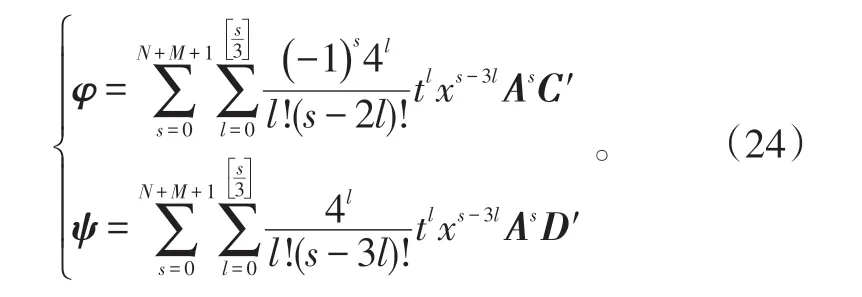
相应的，

式中，j=1,2,…,N+M+2。

取c′1=d′1=1，c′j=d′j=0()

j=2,3,…,N+M+2，有：

从式（25）中可知φj=(-1)j-1ψj，从而可推知g=h即q=r，这样可以得到定理4。

定理4：等谱非线性mKdV 方程（4）有双Wronskian形式的有理解：

其中，φj和ψj满足式（25）。

3 结论

在本文中，通过等谱AKNS 方程的约化，分别构造出Schrodinger 方程，mKdV 方程的新双Wronskian解，并推导出它们各自双Wronskian形式的有理解。

[1]GARDER C S，GREEN J M，MIURA R M.Method for solving the KdV equation[J].Physical Review Letters，1967，19：1095-1907.

[2]WADATI M，SANUKI H，KONNO K.Relationshios among inverse method，backlund transformation and infinite number of conservation laws[J].Progress Theoretical Physics，1975，53：419-436.

[3]HIROTA R.Exact solution of the KdV equation for multiple collisions of solitons[J].Physical Review Letters，1971，27：1192-1194.

[4]FREEMAN N C，NIMMO J J C.Soliton solutions of the KdV and KP equations：the Wronskian technique[J].Physics Letters A，1983，95：1-3.

[5]NIMMO J J C，FREEMAN N C.A method of obtaining the soliton solution of the Boussinesq equation in terms of a Wronskian[J].Physics Letters A，1983，95：4-6.

[6]NIMMO J J C.Soliton solutions of three different-difference equations in Wronskian form[J].Physics Letters A，1983，99：281-286.

[7]ABLOWITZ M J，SEGUR H.Soliton and the inverse scattering transform[M].Philadelphia：The Society for Industrial and Applied Mathematics，1981：15-18.

[8]陈登远，张大军，毕金钵.AKNS 方程的新双Wronskian解[J].中国科学A辑：数学，2007，37（11）：1335-1348.

CHEN DENGYUAN，ZHANG DAJUN，BI JINBO.New double wronskian solutions for the AKNS equations[J].Science in China Series A:Mathematics，2007，37（11）：1335-1348.（in Chinese）

[9]YIN F M，CHEN D Y.Generalized double Wronskian solutions for the third-order AKNS equations[J].Chaos，Solitons and Fractals，2009，39：926-932.