基于改进相似度的混合型多属性决策方法

张 峰，谢振华，林 健，程江涛，崔高仑

（1.海军航空工程学院青岛校区，山东青岛266041；2.91033部队，山东青岛266071）

多属性决策主要解决具有多个属性（指标）的有限方案决策问题，其实质是利用已有的决策信息通过一定的方式对有限个备选方案进行排序并择优，在工程设计、经济、管理、军事等诸多领域具有广泛的应用背景。由于决策环境的复杂性和认知的局限性，决策者有时难以对各种属性值给出精确的评价信息[1]。一般情况下，决策者所给出的评价信息有的能够用精确值表示，有的只能用区间数或者直觉模糊数表示，还有的采用模糊语言变量表示会更合理。这种属性值包含多种数据形式的决策问题就是混合型多属性决策问题。

有关单一型多指标决策问题的研究已经取得了相当丰富的成果，然而混合型多指标决策问题的研究还很不完善。文献[2]采用TOPSIS法处理混合型多属性决策问题，在处理不同属性类型值到理想值的距离时，使用完全不同的计算方法值得商榷。此外，由于距离正理想解近的方案未必距离负理想解远，方法存在适应性问题。文献[3]基于相对熵权和投影算法，定义了相对熵权和贴进度概念，依据投影算法对不同方案进行了排序。李武和胡华南等针对决策者给出的基数评价信息或序数偏好的情形建立了多种多属性群决策模型[4]。文献[5]引入直觉模糊数的得分函数对方案进行了排序，但此得分函数不能进行柔性决策，存在着一定的局限性。文献[6]利用相似度的概念通过引入虚拟正、负理想方案p*和p*，建立各方案与它们之间的相似性测度，帮助决策者识别不同方案的优劣，并通过模糊大多数的概念集结群体意见，为方案优劣排序构建了新的程序和方法，但此方法涉及到的参数赋值主观性较强。文献[7-8]定义了“无差异”和“控制”是排列模糊数字的两个重要概念，为模糊数的相似度计算提供了一种新的方法。文献[9]中以Slonim为代表的学者提出了区间相似度算法，对2个区间的相似性问题进行算法研究，该项研究的结果能给出2个区间值的相似性量化结果，但此方法的区分度较差。因此，本文提出了一种改进的区间相似度方法，以便在提高计算结果区分度的同时，计算结果准确。

1 混合多属性决策问题的描述

多属性决策模型为：

1）方案集S={S1,S2,…,Sm}；

2）属性集P={P1,P2,…,Pn}；

3）属性权重集合ω={ω1,ω2,…,ωn}，其中，

4）决策矩阵A=[aij]m×n，aij是方案Si在属性Pj下的评价值，aij的取值可以是实数、区间数和语言数。

2 基于改进相似度的混合型多属性决策法

2.1 各种属性值相似度问题

定义1：设ℝ+为实数集，对于任意的x1,x2∈ℝ+，若x1＜x2，则称x1和x2的相似度可表示为

定义2：令表示实数轴上的一个闭区间，则称为正区间数。

定义3：称为区间型正理想点，为区间型负理想点，若指标为效益型指标，则：

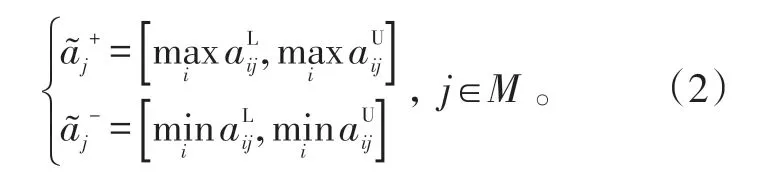
若指标为成本型指标，则交换max 和min的运算符。

文献[10]从集合论的思想出发，用2个区间的长度及其重叠区域的长度表示其相似度，表达式为

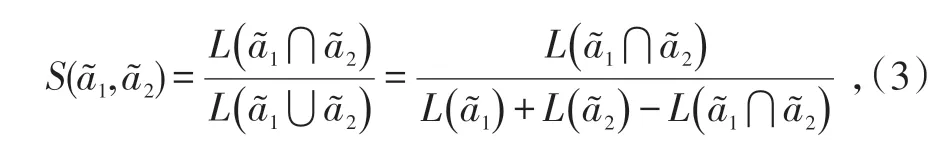
该方法易于理解，形象直观，它反映了2个固定长度的区间，如果重叠部分越多，则其相似度越大。但是，若2个待比较区间均与比较区间没有重叠部分，则依据此方法计算所得的相似度均为0，因而该方法区分度很差。为解决此问题，现将待比较区间与比较区间的相似度计算公式进行改进，图1为2个区间的位置关系。

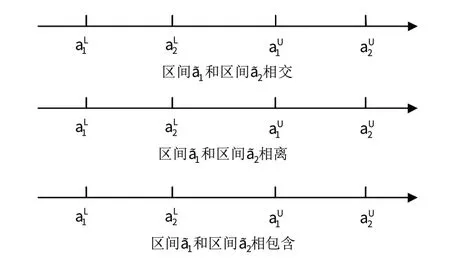
图1 2个区间的位置关系Fig.1 Ubiety relation of two interval numbers

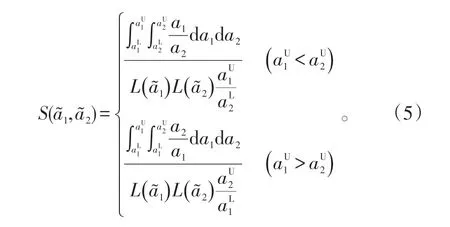
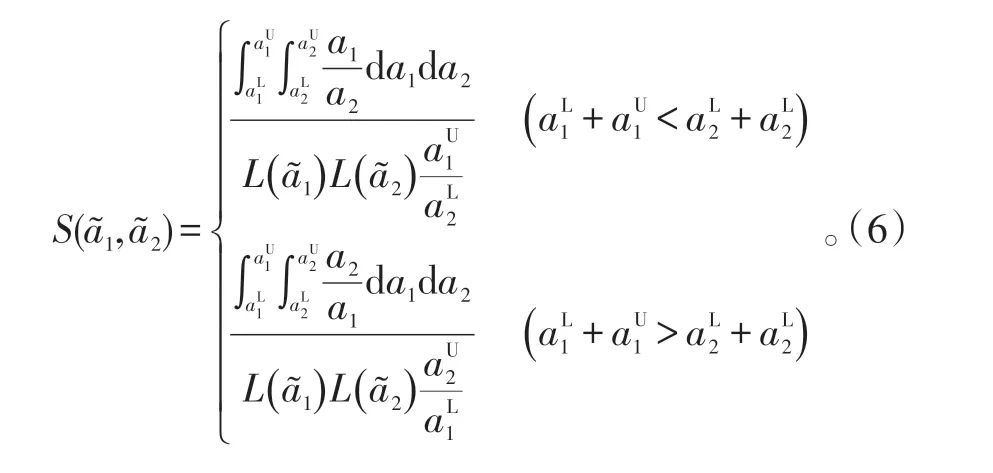
4）若b ∈ℝ+为正区间数，则：

1）非负性，0＜S(X,Y)≤1，S(X,Y)=1 ⇔X=Y；

2）对称性，S(X,Y)=S(Y,X)；

3）等价性，S(X,Y)=1，且S(Y,Z)=1 ⇔S(X,Z)=1；

4）三角不等式，S(X,Y)⋅S(Y,Z)≤S(X,Z)。

2.2 决策方法与步骤

Step 1：方案属性值的规范化。为了消除不同物理量纲对决策结果的影响，就必须对各方案中不同类型的属性值进行规范化。

文献[11]给出了11 标度的语言变量与Vague 数（实质为直觉模糊数）的对应关系。

设语言变量集合S={绝对好，很好，好，较好，中好，中等，中差，较差，差，很差，绝对差}，则对应的直觉模糊数集合为L={（1，0，0），（0.9，0.05，0.05），（0.8，0.1，0.1），（0.7，0.15，0.15），（0.6，0.2，0.2），（0.5，0.5，0），（0.4，0.4，0.2），（0.3，0.55，0.15），（0.2，0.7，0.1），（0.1，0.85，0.05），（0，1，0）}。

依直觉模糊数转化为区间数的公式：

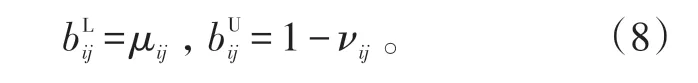
Step 2：构建第i个待评方案、正理想解方案和负理想解方案向量。

Step 3：计算方案i的属性j与正、负理想方案的属性j的相似度。具体可依式（4）～（7）而为。

Step 4：计算方案i的属性j与正、负理想方案属性j的属性关联度为：

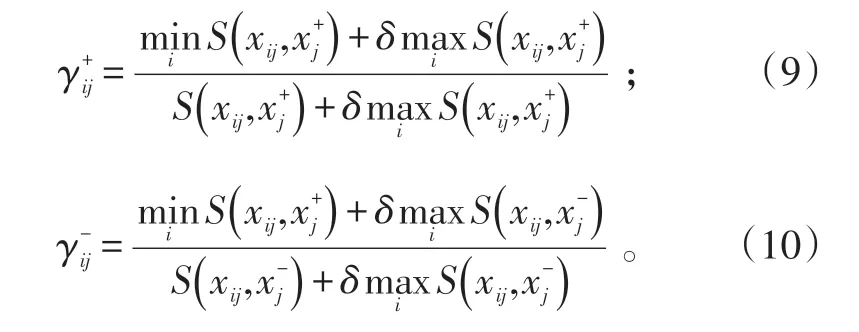
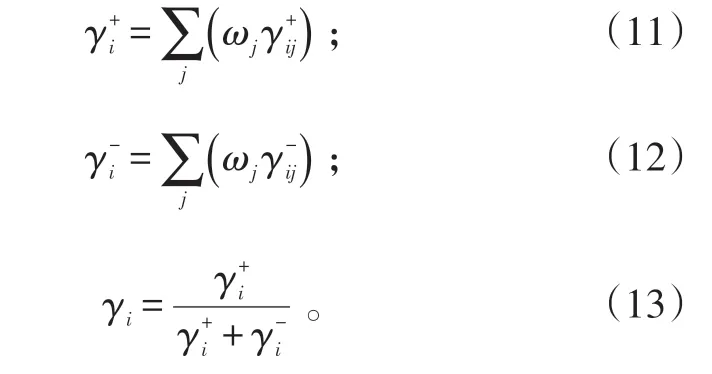
式（11）～（13）中：ωj为属性j的权重。

Step 6：将综合关联度γi从大到小排序，所得结果即为各方案的优劣顺序。

3 算例

为了便于对比分析，本文采用文献[1]中的实例进行分析。实例：某国国防部拟发展一种战术导弹武器，研制部门提供了4种导弹型号的有关信息，指标权重已经由相关专家详细考察得出，结果见表1。

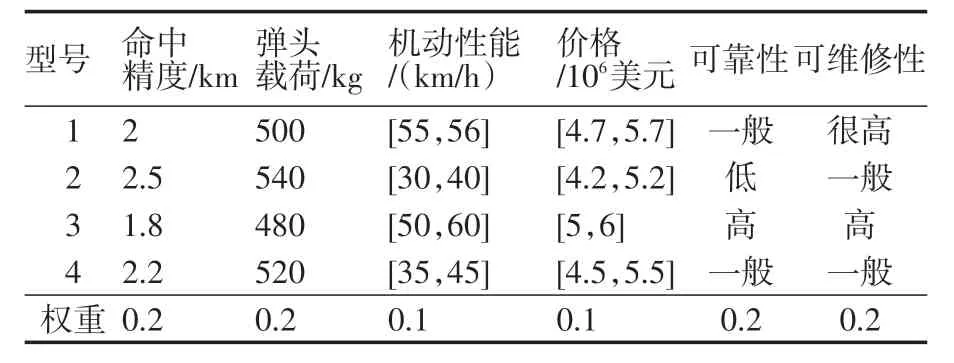
表1 4种不同型号导弹武器性能指标Tab.1 Performance indices of four kinds of missile weapon

经计算得方案1～4的综合关联度（δ=0.3）分别为0.515 8、0.464 0、0.540 7、0.474 9。排序：方案3 ＞方案1 ＞方案4 ＞方案2，故最佳方案为方案3，各方案综合关联度见表2。文献[1]采用TOPSIS法来求解，其结果相同。文献[12]采用基于直觉模糊数法进行决策评估，其结果也相同。因此，采用基于改进相似度的混合型多属性决策方法进行评估计算是可行的。

表2 4种不同型号导弹方案的综合关联度Tab.2 Comprehensive correlative of four kinds of missile weapon

4 结论

鉴于目前混合型多属性决策问题的研究还很不完善，本文基于将难以定量描述的语言属性指标转化为定量描述的区间型属性指标的目的，引入相似度概念，考虑到若2个待比较区间均与比较区间没有重叠部分时，依据现有的区间相似度计算方法难以衡量两者与比较区间相似度的问题，对现有的区间相似度计算方法进行了改进，依据改进后的相似度计算模型对原有案例进行了计算，结果与基于TOPSIS 法和直觉模糊数法所得的结果一致，在一定程度上说明了改进后的方法的正确性。改进后的相似度计算模型可以处理任何区间之间的相似度问题，并解决了区分度差的问题。但是，在将语言型指标转化为区间型指标时，难免会损失一定的信息量，在方案属性值比较接近时，依据本方法得出的结果或可能不够精确，今后应在这方面开展一定的研究。

[1]HWANG C LAND，YOON K.Multiple attribute decision making：methods and applications[M].New York：Springer-Verlag，1981：1-10.

[2]夏勇其，吴祈宗.一种混合型多属性决策问题的TOPSIS方法[J].系统工程学报，2004，19（6）：630-634.

XIA YONGQI，WU QIZONG.A technique of order preference by similarity to ideal solution for hybrid multiple attribute decision making problems[J].Journal of Systems Engineering，2004，19（6）：630-634.（in Chinese）

[3]RAO CONGJUN，PENG JIN，ZHANG ZHONGCHENG.Method of hybrid multi-attribute decision making based on relative entropy weight and projection algorithm[C]//Proceedings of the 7th World Congress on Intelligent Control and Automation.Chongqing：IEEE Robotics and Automation Society，2008：7500-7504.

[4]LI WU，ZHANG XIAOMEI，CHEN YAN.Information integration approach to vendor selection group decision making under multiple criteria[J].Lecture Netes in Computer Science，2009（1）：1138-1143.

[5]卫贵武.对方案有偏好的直觉模糊数多属性决策方法[J].科技管理研究，2008（8）：171-173.

WEI GUIWU.Method of intutionistic fuzzy multiple attribute decision making with preference relation on alternatives[J].Science and Technology Management Research，2008（8）：171-173.（in Chinese）

[6]郭强，郭耀煌，郭春香.基于模糊相似度的群决策方案排序[J].西南交通大学学报，2010，45（2）：307-311.

GUO QIANG，GUO YAOHUANG，GUO CHUNXIANG.Alternative ranking based on fuzzy similarity in group decision-making[J].Journal of Southwest Jiaotong University，2010，45（2）：307-311.（in Chinese）

[7]TSENG TY，KLEIN CM.A survey and comparative study of ranking procedures in fuzzy decision-making.881201[R].Columbia：Department of Industrial Engineering，University of Missouri Columbia，1988.

[8]TSENG TY，KLEIN CM.New algorithm for the ranking procedure in fuzzy decision-making[J].IEEE Transactions on Systems Man and Cybernetics，1989，19（5）：1289-1296.

[9]SLONIM T Y，SCHNEIDER M.Design issues in fuzzy case-based reasoning[J].Fuzzy Sets and Systems，2001，117（2）：251-267.

[10]秦玉平，杨兴凯.基于案例推理的区间属性相似度研究[J].辽宁师范大学学报，2006，29（4）：442-445.

QIN YUPING，YANG XINGKAI.Study of range attributes similarity of case-based reasoning[J].Journal of Liaoning Normal University，2006，29（4）：442-445.（in Chinese）

[11]周晓光，张强，胡望斌.基于Vague 集的TOPSIS方法及其应用[J].系统工程理论方法应用，2005，14（6）：537-541.

ZHOU XIAOGUANG，ZHANG QIANG，HU WANGBIN.Research on TOPSIS methods based on vague set theory[J].Systems Engineering-Theory Methodology Applications，2005，14（6）：537-541.（in Chinese）

[12]司艳杰，魏法杰.基于直觉模糊优选模型的混合型多属性决策[J].系统工程与电子技术，2009，31（12）：2893-2897.

SI YANJIE，WEI FAJIE.Hybrid multi-attribute decision making based on the intuitionistic fuzzy optimum selecting model[J].Systems Engineering and Electronics，2009，31（12）：2893-2897.（in Chinese）