圆锥参数测量辅具的设计

刘兴富　刘瑞玲

(1广州威而信精密仪器有限公司，西安 710075；陕西五环(集团)实业有限责任公司，西安 710038)

0　引言

圆锥结合在机械、仪器及工具等结构中应用广泛，实现圆锥结合的互换性，对提高产品质量、降低生产成本，具有重大意义。

圆锥与圆柱相比，圆锥结合有如下一些特点：

1)能保证结合件相互自动对准中心，它不仅能使结合件的轴线重合得很好，而且经多次装拆亦不受影响；

2)配合间隙或过盈的大小可以调整，通过调整内、外圆锥的轴向相对位置，得到不同性质的配合，延长零件的使用寿命；

3)配合紧密而又便于装拆，具有自锁性能，能够传递一定的扭矩，传动装置结构简单紧凑，加工和装配方便，经济性好。

圆锥参数的测量，如何正确选择测量方案和正确评定圆锥零件的质量，是提高圆锥零件质量，保证互换性不可缺少的环节。

圆锥参数一般包括：圆锥角a (或锥度C)、大端直径D、小端直径d和锥体长度L等。笔者将以零件实例，讨论圆锥参数在加工过程中的具体测量方法。在大批量生产中内、外圆锥零件参数的测量，既要求准确可靠，又要求能在生产现场随时测量。准确、便捷、高效率的测量方法，是提高内、外圆锥零件质量的保证。

通常内、外圆锥零件参数的测量方法有：

量规法、涂色法。将内、外锥涂色与圆锥塞、环规相接触，根据接触长度判断被测内、外圆锥角是否合格。这种方法要求测量者经验丰富，且不知道内、外圆锥各参数的实际值；

仪器测量法、正弦规测量法。方法成本和环境条件要求高，测量过程比较复杂，不适合在车间现场测量。

本文采用辅具测量圆锥零件的参数，并对现场实用测量辅具的设计方法，进行了详细论述。

1　内、外圆锥角的测量

内、外圆锥角测量辅具均是根据如图1a所示的圆柱测量外锥斜角的正切原理设计，即

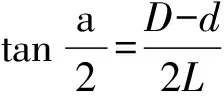
(1)

式中，a 为圆锥角；C为锥度值C=2tan(a /2)。

辅具结构设计如图1b、c所示：均采用钢球环结构，一组钢球用隔离架与内、外环固定成一体，固定环与活动环应具有一定的弹性，以使它们很好地与被测圆锥接触。测量元件采用测微表或计量传感器。

图1　内、 外锥辅具设计

当辅具的测量元件选用测微表时，应将被测内、外圆锥角a 的变化量Δa ，转化为固定环和活动环测球中心之间距离L的变化值ΔL。这样就将复杂圆锥角的测量转化为简单的长度测量。运用锥度公差计算比锥角计算简便，为此，对式(1)微分得

(2)

在此，将本文设计给出锥角及锥角公差，换算为锥度及锥度公差：

将内锥：a /2=3°20′，Δa /2=±1′，D=25.4mm,d=20.64mm,及外锥：a /2=3°30′，Δa /2=±1′，D=26.10mm，d=19.70mm代入式(1)、式(2)得

内锥：C=0.116401,外锥：C=0.122399。

内锥、外锥：ΔC=±0.0003。

内锥：L=40.893mm,ΔL=±0.105mm； 外锥：L=52.288mm，ΔL=±0.128mm。

测量时，先用6°40′标准圆锥塞规、7°标准圆锥环校对测微表的“零位”，这时，测微表的零位与内锥6°40′相对应、与外锥7°相对应。

当辅具的测量元件选用计量传感器时，可以将计算通过软件硬化在芯片里，直接显示锥度偏差和锥角偏差。

2　内、外圆锥直径的测量

2.1　锥孔大端直径的测量

1)将径向转化为轴向的测量

锥孔大端直径采用通用量具测量误差大，不能保证测量精度要求。如图4圆锥零件的锥孔大端直径为Ф300+0.052，公差仅为0.052mm。为此，将径向尺寸测量转化为轴向尺寸测量，用专用量具—卡规和标准圆锥塞规配合测量，简单、直观、方便，测量原理如图2所示。

图2　测量原理

2)计算公式的推导

设锥孔锥角为a ，那么斜角为a /2，当锥孔直径尺寸变化量(直径公差)为ΔD时，计算轴向尺寸变化量(轴向尺寸公差)ΔH

由图3几何关系可得

(3)

(4)

图3　测量锥孔大端直径的专用量具—标准塞规

式(4)就是计算轴向尺寸变化量的通式，当圆锥以锥度标注时，计算更为简便。

3)测量方法

如图3所示，可以在塞规大端端面磨一个台阶，台阶高等于轴向尺寸公差ΔH。检查工件端面是否在此台阶高度内，即可确定锥孔大端直径是否合格。

2.2　圆锥大、小端直径的测量

圆锥大、小端直径的测算方法相似(求解过程相同)，测算步骤和方法如下：

如图4所示，测量辅具由基座、标准圆柱、外径千分尺组成。先用直径为 d的标准圆柱，测出如图4a和图4b的尺寸m1,由几何关系得

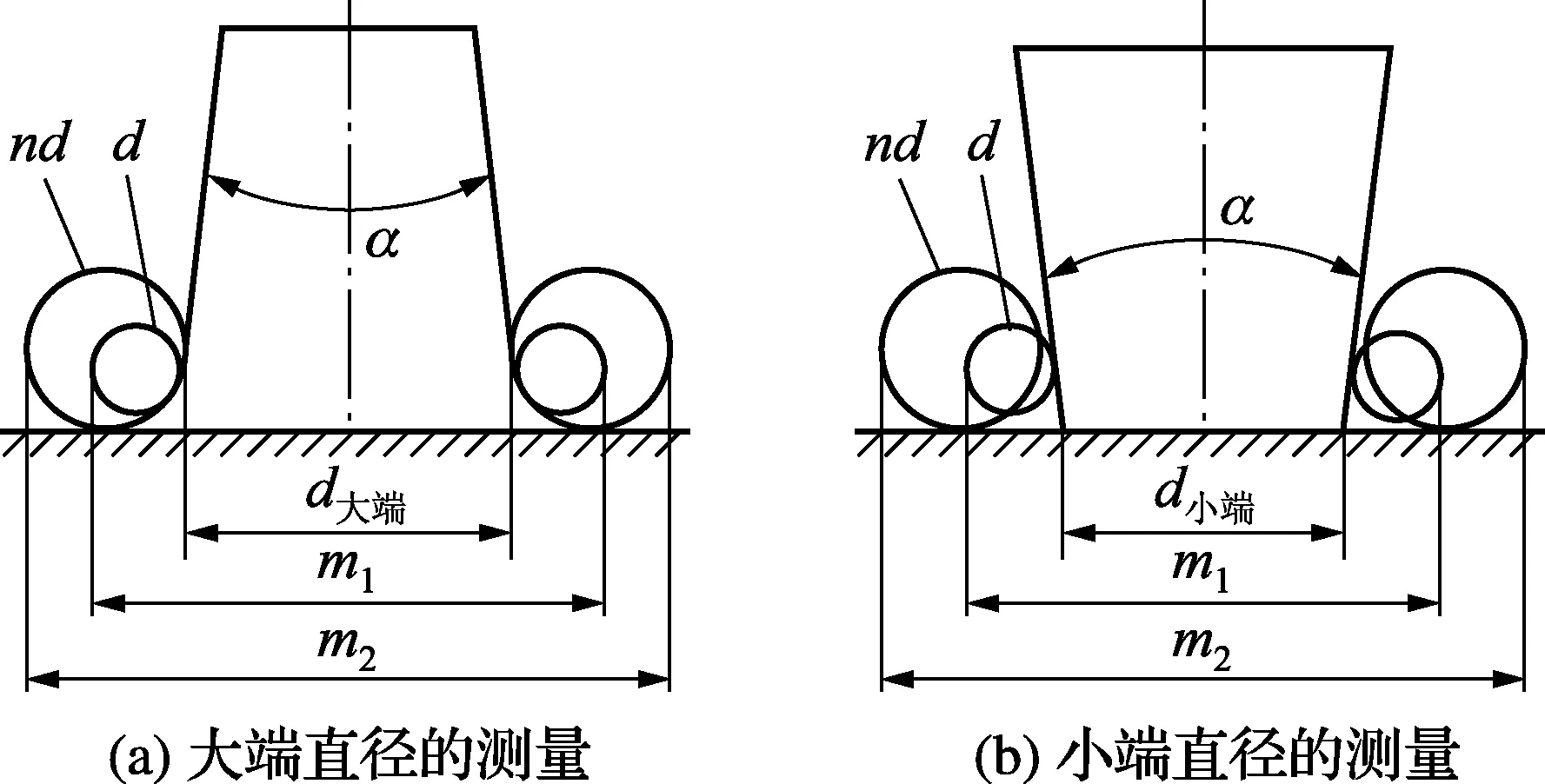
图4　圆锥大、小端直径的测量

(d大端用正号，d小端用负号)

(5)

再以直径为 nd的标准圆柱，测出图5a和图5b所示的尺寸m2，则

(d大端用正号，d小端用负号)

(6)

由式(5)乘以n 减 式(6)得

(7)

n 可以取为任意值，在此，笔者取大、小标准圆柱直径之比，即n=nd/d，代入式(7)后可得

(8)

对式(8)等式两端求导(把标准圆柱直径看作常量)：

式中,Δd大端(Δd小端)为被测圆锥大、小端直径

(9)

从式(9)可以看出，标准圆柱的直径，直接影响着测量精度。为了减小标准圆柱直径对被测圆锥大、小端直径测量精度的影响，应尽量选取较小的标准圆柱直径，且大、小标准圆柱直径应为相近的适当值。笔者将标准圆柱nd取φ4mm，标准圆柱d取φ3mm的圆柱直径分别进行(二次)测量。

令式(9)中的nd-d=1，则式(9)可简化为

Δd大端(Δd小端)=nd·Δm1-d·Δm2

(10)

对式(10)进行分析可知，Δd大端(Δd小端)直径的测量误差，与两次测量时大(nd)、小(d)圆柱直径及它们的直径差值有关：标准圆柱的直径及大、小差值越大，对Δd大端(Δd小端)直径的测量影响也越大。

从测量实际考虑，m1、m2是用同一计量器具，对相同的尺寸段的两次测量，故有

Δm1=Δm2=Δm

则

(11)

从式(11)可知，当取大(nd)、小(d)圆柱直径的差值等于1时，Δd大端(Δd小端)直径的测量准确度，仅与选用计量器具的误差有关。

最后应指出的是，本文方法只增加了一次测量，就大大简化了已往方法参数的计算，使计算式不含角度参数，并采取大(nd)、小(d)圆柱直径的差值等于1，来避免角度误差，减小圆柱直径对圆锥大、小端直径测量准确度的影响。

3　结束语

辅具根据精度要求，指示表可选用百分表或千分表。辅具结构简单，一般中小型机械厂都可以自制。辅具可实现车间现场随时测量，准确可靠，轻巧耐用，完全能满足生产现场测量要求。

[1]张玉文，唐家才.角度测量.中国计量出版社，1998

[2]陈于平，高晓康.互换性与测量技术.高等教育出版社，2004

[3]王伯平,主编.互换性与测量技术基础.机械工业出版社，2005

[4]胡晓昌.自制盲孔检具的应用.计量技术，2010(3)