高温双毛细管粘度计恒温系统研究*
刘 灿 林 鸿 冯晓娟 李晓苇 张金涛
(1.河北大学物理科学与技术学院,保定 071002;2.中国计量科学研究院热工计量科学研究所,北京 100013)
0 引言
热力学温度是国际单位制中七个基本单位之一,热力学温度的准确测量是制定或修订国际温标的基础。当前,国际温度计量缺乏600~1360K温度范围准确可靠的热力学温度测量值[1]。本文部分作者的探索研究结果表明,声学共鸣法的温度测量上限可提高至1360K[2]。声学温度计的工作原理是[3],通过测量理想气体声速获得代表声学动能的热力学温度。实际气体区别于理想气体,其粘滞性对理想声学动能有耗散作用,是气体声学温度计测量最大不确定度来源[4]。因此,准确地掌握气体声学温度计工作气体介质的粘度,是获得准确的热力学温度值的关键之一。在高于90K的温度范围,氩气被认为最适合于作为声学气体温度计的工作介质[3],但满足声学温度计准确度要求的氩气粘度值温度范围限于常温附近。当前,采用量子物理“从头算”方法,可以获得1~1000K范围氦气的粘度[5],计算不确定度小至0.001%。毛细管粘度计以及由此所发展的双毛细管粘度计[6-8],结合量子化“从头算”得到的氦气粘度值,在400K以下温度范围,可准确地获得其它被测气体的粘度[9-11],测量不确定度达到0.02%,独立实验结果[9, 11]的不一致性为0.025%。Vogel给出了氩气“从头算”的粘度值[12],但其计算不确定度未评估。在400K以上温区,缺少不确定度接近0.1%的实验测量值。
我们在已有工作基础上[11,13],设计建立400~700K双毛细管粘度计实验系统,用于开展该温度范围氩气粘度准确测量。该系统是全球首个高温双毛细管粘度计实验装置。如文献介绍,双毛细管粘度计由参考段(温度被控制在293.15K)和测量段构成,测量段温度可调节。因此,将测量段和参考段均匀稳定地控制在设定温度,是双毛细管粘度计准确测量的技术关键。本文介绍了为该高温双毛细管粘度计实验系统设计的恒温装置,开展的控温研究和所获得的控温效果。
1 恒温装置
图1为高温双毛细管粘度计实验系统简图。
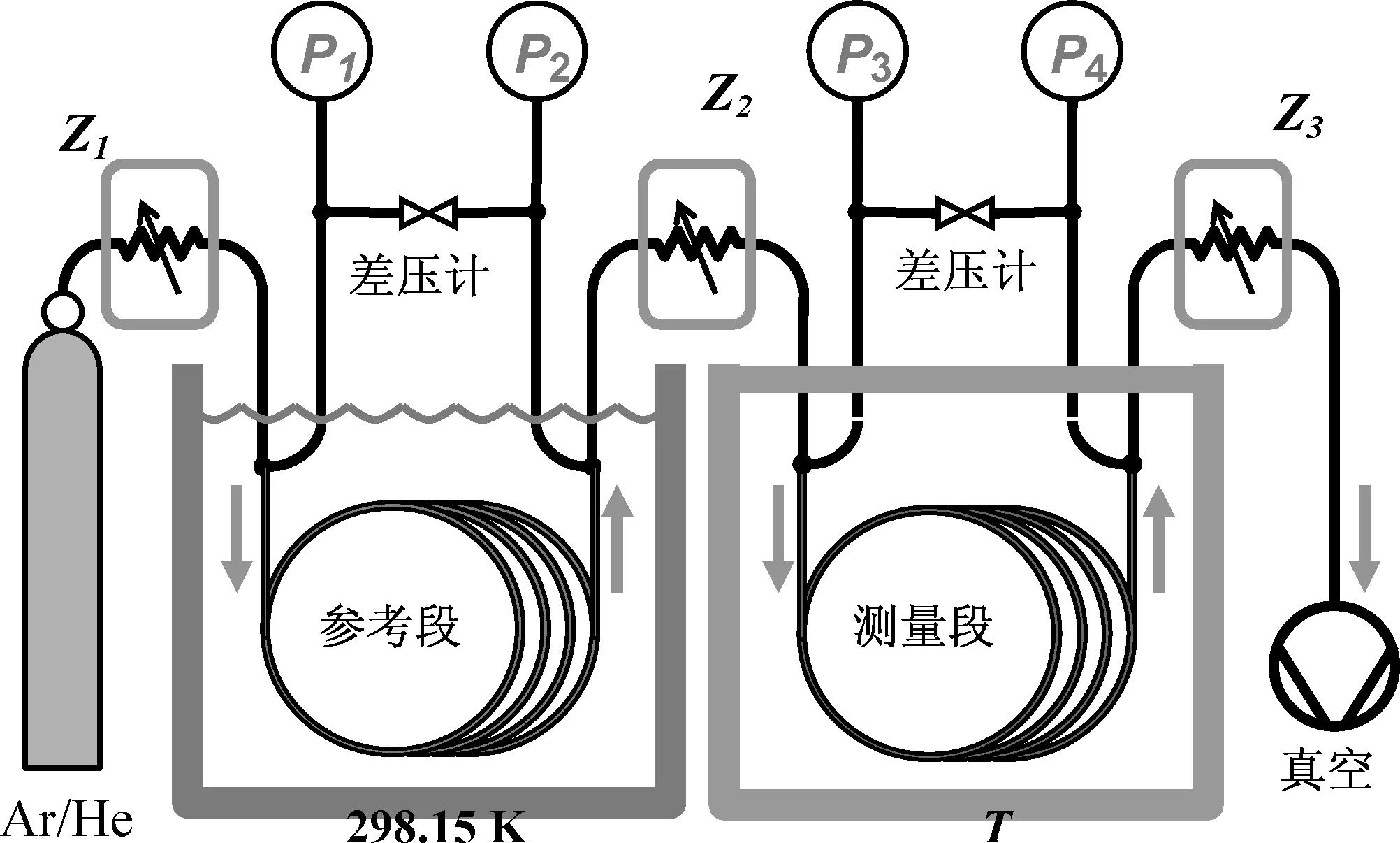
图1 400~700K双毛细管粘度计实验系统图

1、2、3:一等标准铂电阻温度计;4:高温烧结炉;5:保温棉;6:外加热圈;7:外均温铝管;8:内均温铝管;9:沿内均温铝管外柱面一圈加工的矩形凹槽;10:内加热圈
其中参考段毛细管放置在298.15K的恒温酒精槽内,与文献[11]所介绍的参考段完全等同。本文专注于测量段实验系统建立及其控温方法研究。提出并设计了如图2所示双铝管恒温系统,图中高温箱式烧结炉的最高工作温度为1100℃,温度波动不超过±1℃,为炉内双铝管恒温装置提供较为稳定的温度环境。双铝管恒温装置外层包裹约20mm厚的保温棉,以消减高温炉内温度波动对双铝管温度的影响,改善恒温的稳定性和均匀性[14]。在高温炉提供的相对稳定的温度环境下,使用STANFORD RESEARCH SYSTEMS控温器PTC 10,配合一等标准铂电阻温度计,对双铝管恒温装置进行精确控温,双铝管内外双层加热元件为带状不锈钢加热圈,电阻分别为80Ω和120Ω。
图2中6~10为恒温系统的核心部分,是一套内、外双铝管恒温装置,其截面如图3所示。该恒温装置包括内、外均温铝管和内、外加热圈,均温铝管件经过精密加工。内铝管壁厚15mm,长120mm,内径128mm,铝管中部外表面开矩形槽,槽深2mm,宽82mm,毛细管在内铝管矩形槽内的布置方式如图4所示。外铝管壁厚15mm,管长120mm,内径158mm。内、外均温铝管上的温度计插孔深度为50mm。

1、2、3分别为图1中温度计1、2、3的插孔;6、7、8、9、10即图2中的6、7、8、9、10部分

图4 毛细管在内铝管矩形槽内的布置方式
与常规恒温方式[15]相比,双铝管法采用内外加热圈同时传送热量控温,热量传递路径短,传热速度快,装置内部温度对控制器调节的响应快,有利于恒温控制和减少轴向和径向温度梯度[16]。
2 控温
2.1 控温环境
将外部环境温度稳定在比控制目标温度稍微低一些的值上,减弱炉内温场对恒温装置内部温场的影响,有利于双铝管恒温系统获取好的控温效果。
我们在双铝管恒温系统外设置了保温棉结构,该结构采用保温棉-薄铝板-保温棉-薄不锈钢板结合形式,有效地降低了高温炉和恒温装置内部的热交换,以利用控温器精细调节。
2.2 PID整定
2.2.1PID控温原理[17]
PID(Proportion-Integral-Differential)指比例-积分-微分。PID温度控制的公式为:
(1)
式中:u(t)为控制器输出功率;kP为比例系数;ΔT(t)为t时刻控温目标温度与系统实际温度的差值;kI为积分系数;kD为微分系数。
比例、积分和微分系数越大,相应的作用越强。
2.2.2PID整定方法
PID整定是指选取合适的比例系数、积分系数和微分系数,使被控制量的波动幅度和稳态误差满足使用要求。工程上有很多PID整定方法,如临界比例度法,衰减曲线法和经验试凑法等等。在实际整定PID过程中,我们需要视被控温对象的特征来选取合适的整定方法。
本文恒温装置系统具有以下特点:保温层热阻大,内外换热慢;双铝管具有很大的热惯性;控温目标温度和高温炉内工作温度一致,和高温炉内温度的温差ΔT很小。
在绝热性好的被控系统,温度上升过程与下降过程非常不对称,温度上升沿很陡,温度下降沿很平缓,降温时间长,因此选取合适的kP来避免温度超调是至关重要的。通过对kP反复的整定,总结了kP值对本装置控温温度曲线的影响,如图5所示。

图5 kP对控温曲线的影响
积分项用来消除系统的稳态误差,kI过大,会造成系统震荡和温度超调。kI过小,系统的稳态误差不能完全消除。
对于绝热性好的控温装置,控温环境非常稳定,被控对象温度不会出现大的突变,不需要微分项来调节。
2.2.3PID整定过程
1)kP参数整定
将控温目标温度与实际温度温差ΔT设定在3~5℃,高温炉工作温度和控温目标温度基本保持一致,将kP设定为较小值(5至10之间),控温开始后,观察温度变化曲线,如果无超调,记录从控温开始至温度稳定过程的时间,然后重复前述步骤,直至整定出合适的kP值,升温速度快,且无超调,稳态误差保持在10~20mk。如果出现超调,立刻停止控温,重新设定控温目标温度和高温炉工作温度,保持原来的温差不变,减小kP,直至无超调出现,重复前述无超调的步骤,直至整定出合适的kP。
2)kI参数整定
整定好kP参数后,先设定较小的kI,然后逐渐增加kI,每设定一个kI后等待温度稳定,观察稳态温差的变化情况。待稳态温差消除,便整定出kI参数。
3 实验结果
开展了室温至400℃的控温实验,图6 给出了400℃控温温度。5h内,三支温度计在25℃、200℃和400℃的温度波动度分别为±0.001℃、±0.002℃和±0.003℃。温度计1和3表示内铝管温度不一致性,在25℃和200℃下,小于±0.002℃, 400℃下,为±0.004℃。

图6 400℃温度曲线
温度计2、3的平均值和温度计1的差异体现毛细管工作区内、外铝管径向温度不一致性,在25℃和200℃下,温差不超过0.003℃,在400℃下,不超过0.005℃。
4 讨论和总结
本文介绍了作者为高温双毛细管粘度计设计的400~700K温度范围精密控温装置。根据我们选择的优化PID参数,在400 ~700K温区,5h内恒温装置温度稳定性好于±3mK,轴向温差优于±4mK,径向温差小于5mK,可满足高温双毛细管粘度计,在400~700K测量气体介质粘度扩展不确定度优于0.1%的技术要求。
[1]Ripple D C, Strouse G F and Moldover M R. Acoustic thermometry results from 271 to 552 K[J]. Int J Thermophys, 2007, 28: 1789-1799
[2]Feng X J, Gillis K A, Moldover M R, et al. Microwave-cavity measurements for gas thermometry up to the copper point [J]. Metrologia, 2013, 50(3): 219-226
[3]M R Moldover, R M Gavioso, J B Mehl, L Pitre, M de Podesta, J T Zhang.(2013) Acoustic Gas Thermometry (Metrologia接收)
[4]Zhang J T, Lin H, Feng X J, et al. Progress toward redetermining the Boltzmann constant with a fixed-path-length cylindrical resonator. Int. J. thermophys. 2011, 32(7-8): 1297-1329
[5]Cencek W, Przybytek M, Komasa J, et al. Effects of adiabatic, relativistic, and quantum electrodynamics interactions on the pair potential and thermophysical properties of helium[J]. The Journal of Chemical Physics, 2012, 136: 224-303
[6]Berg R F. Quartz capillary flow meter for gases[J]. Review of scientific instruments, 2004, 75(3): 772-779
[7]Berg R F. Simple flow meter and viscometer of high accuracy for gases[J]. Metrologia, 2005, 42(1): 11-23
[8]Berg R F. ERRATUM: Simple flow meter and viscometer of high accuracy for gases[J]. Metrologia, 2006, 43: 183
[9]V May E F, Moldover M R, Berg R F, et al. Transport properties of argon at zero density from viscosity-ratio measurements[J]. Metrologia, 2006, 43(3): 247
[10]May E F, Berg R F, Moldover M R. Reference viscosities of H2, CH4, Ar, and Xe at low densities[J]. International Journal of Thermophysics, 2007, 28(4): 1085-1110
[11]Zhang J T, Lin H, Che J. Effects of connecting tubing on a two-capillary viscometer[J]. Metrologia, 2013, 50(4): 377
[12]Vogel E, et al.Ab initio pair potential energy curve for the argon atom pair and thermophysical properties for the dilute argon gas. II. Thermophysical properties for low-density argon[J]. Molecular Physics, 2010. 108(24): 3335-3352
[13]车晋, 林鸿, 高林虎, 等. 测量理想气体状态下气体输运性质的双毛细管粘度计研究[J]. 电子测量与仪器学报, 2013, 27(2):167-172
[14]杨宇, 李宏生, 施峥嵘. 高精度恒温槽设计[J]. 仪表技术, 2005(5): 63-65
[15]王震森,马洪其. 80~500℃温度计精密校验装置[J]. 自动化仪表, 1994,8(2): 21-24,48-49
[16]Healy W M, Flynn D R. Thermal modeling of multiple-line-heat-source guarded hot plate apparatus[J]. ASTM SPECIAL TECHNICAL PUBLICATION, 2002, 1426: 79-96
[17]刘金琨. 先进PID控制MATLAB仿真[M]. 北京:电子工业出版社,2011:1

