小端接触同步器后备量分析与验证
王伟
(上海汽车变速器有限公司,上海 201807)
0 引言
同步器系统是动力中断变速器(MT、AMT)和双离合器变速器(DCT)内具有决定性影响的关键总成,同步器系统一般包括齿套、齿毂、滑块、同步环、结合齿等。同步器作用是在换挡时同步输入端与输出端的转速差并在换挡结束后传递扭矩,保证换挡时齿轮啮合不受冲击,使换挡动作方便迅捷,有利于提高汽车的动力性和燃油经济性[1-2]。其后备量是指同步环与结合齿的轴向装配间隙,其目的是保证同步环锥面磨损后仍能有效工作[3-4],如图1所示。
1 传统一维尺寸链计算后备量
在传统分析同步器后备量时,先假设摩擦锥面完全接触,即结合齿和同步环的检测锥点位置完全重合,再利用一维线性尺寸链计算其后备量[5]。图2为传统一维尺寸链计算后备量图,图中xm1±Δxm1为齿轮的左定位面至结合齿右端面的尺寸,xm2±Δxm2为齿轮的左定位面至检测点的尺寸,xm3±Δxm3为齿环左端面至检测点的尺寸。则锥面完全接触下的后备量dx的计算公式
dx=-(xm1±Δxm1)+(xm2±Δxm2)-(xm3±Δxm3)
式(1)中:dm为后备量的名义尺寸。

图1 单锥面同步器系统

图2 传统一维尺寸链计算后备量图
由上述可知,传统一维尺寸链计算后备量未考虑同步环与结合齿锥点接触位置对后备量的影响,这样对于小端接触的同步环来说,其实测值与理论计算存在较大的出入,因此文中采用二维尺寸链计算小端接触同步环的后备量,具体计算方法如下。
2 二维尺寸链图解法计算后备量
由于同步环与结合齿为小端接触,导致接触点与检测点位置不一致,因此后备量需要采用二维尺寸链图解法进行计算[6]。图3为小端接触二维尺寸链计算图,即当结合齿和同步环锥面采用小端接触时,同步环的检测点相对于结合齿的检测点向外平移长度为dc的一段距离。因此小端接触的后备量应比锥面完全接触的后备量多dc这段长度。图3中结合齿的摩擦锥角为θ1,同步环的摩擦锥角为θ2,由于采用小端接触,同步环锥角θ2大于结合齿锥角θ1,结合齿检测点位置A(x2,y2)、齿环检测点位置B(x2+dc,y2),齿环的检测点至接触点的轴向长度为c。

图3 小端接触二维尺寸链图解计算后备量图
图3中结合齿锥面投影的直线方程为
同步环锥面投影的直线方程为
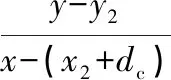
(3)
联立方程(2)(3)即可得出两锥面接触点的x坐标值:
由图3可知,两锥面接触点的x坐标值;
x=x2+dc+c
(5)
联立公式(4)(5)可得:
联立方程(1)(6)可得锥面小端接触下的后备量dt为
dt=dx+dc
由上述可知,对于小端接触的同步器系统来说,采用二维尺寸链计算的后备量大于一维尺寸链计算值,且同步环与结合齿锥面角度差越大,二者差异越大。
3 验证分析
现以某变速器三挡单锥面同步环为研究对象,表1为某一变速器三挡单锥面同步器系统10组实测值,其中第1~5组同步环与结合齿锥面角度差为0.25°~0.32°,为理论设计中上差;第6~10组同步环与结合齿锥面角度差为0.08°~0.13°,为理论设计中下差。

表1 某一小端接触同步器系统实测值
表2是采用上述两种方案理论计算后备量与实测后备量对比。
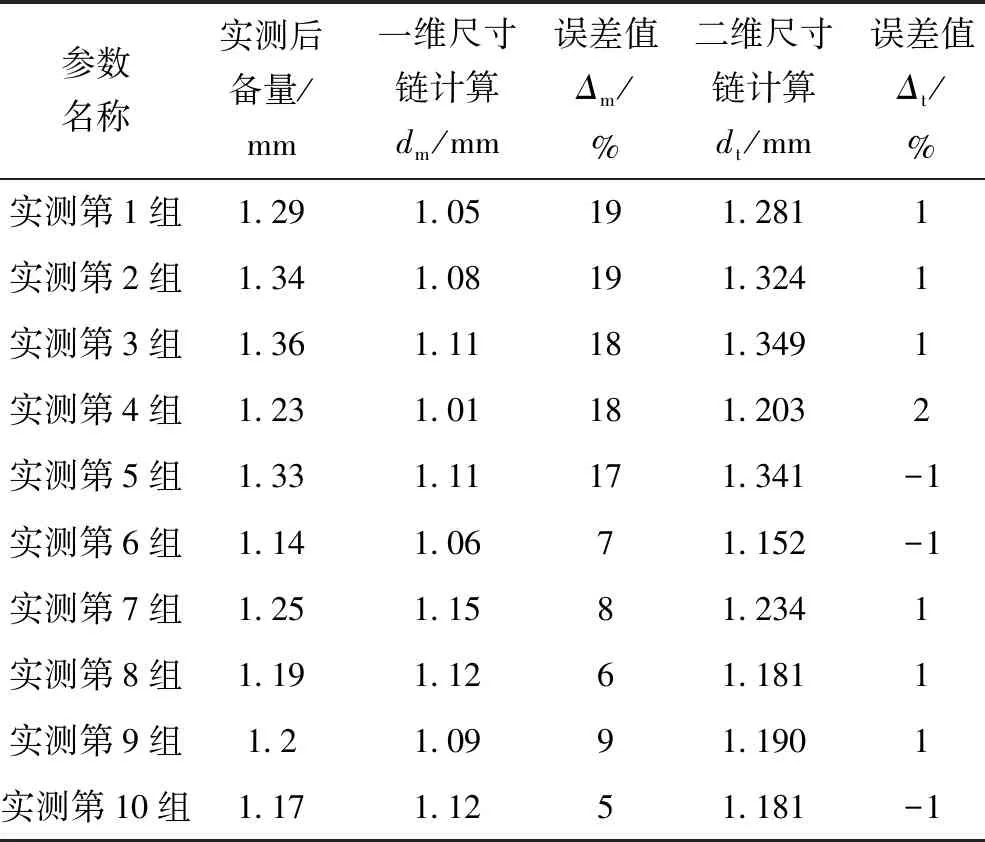
表2 某一小端接触同步器后备量对比分析
通过表2可知:对于锥面角度差较大的第1~5号同步器系统来说,采用一维尺寸链计算的后备量与实测值出入较大,误差为17%~19%;而对于锥面角度差较小的第6~10号同步器系统来说,采用一维尺寸链计算的后备量与实测值也存在一定误差,误差为5%~9%;而对于二维尺寸链分析,不管锥面角度如何分布,其理论计算后备量与实测值接近,误差值为-1%~2%,说明采用二维尺寸链计算的后备量更加准确可靠。
4 结论
(1)对于小端接触的同步器来说,由于同步环与结合齿锥面角度差造成二者接触点后移,因此采用二维尺寸链计算的后备量大于一维尺寸链计算值。
(2)对于小端接触的同步器来说,同步环与结合齿锥面角度差越大,同步器系统后备量越大;同步环的检测点与接触点轴向距离c越大,同步器系统后备量越大。
(3)对于小端接触的同步器来说,实测后备量值与一维尺寸链计算值误差最大达19%,而采用二维尺寸链计算的误差仅-1%~2%,此说明二维尺寸链计算的后备量比较准确可靠。

