一类带有不育控制的单种群离散模型

李秋英， 张凤琴， 刘汉武

(运城学院应用数学系 山西运城044000)

0 引言

鼠类在农、林、牧业等方面造成的损失远大于病害和虫害，它们还是多种病菌的寄主和传播者，因此对害鼠的有效控制越来越重要．随着对鼠类研究的深入，科学家们已经不再局限于研究鼠类对人类生产、生活的危害了，并展开鼠类对于生态系统的影响以及对鼠类的不育控制方面的研究．

不育控制是借助某种技术或方法使雄性或雌性绝育，或阻碍胚胎着床发育，甚至阻断幼体生长发育，以降低生育率，从而控制种群数量的增长［1］．不育控制有许多优点:不会对环境造成污染，具有针对性，能大面积使用，在经济上花费更少，效率更高等［2］．因此公众和动物权益组织认为不育控制是人道的．目前，关于不育控制技术的研究主要分为2方面:一方面为药效的研究即野外控制实验［3］;另一方面为不育控制下害鼠种群动态的系统分析［4－5］．

种群动态的理论分析方面，一些学者采用微分方程模型［5－7］，也有学者采用差分模型研究种群动态．张知彬指出［4］，不育控制之前应从理论上分析，同时建立数学模型，并对其进行分析，预见不育控制下害鼠的种群动态，评价其效果，并提出指导意见．

1 模型建立

本文中，将害鼠种群分为可育者F和不育者S两类．为建立模型，首先做以下假设:

1)生育函数为B(N)=b(1－rN)1r，b ＞0，r＜0．

2)不育控制方式是非自传播方式．

3)单位时间内可育个体和不育个体的死亡率分别为d1，d2(d1，d2＜b)．

4)单位时间内可育个体到不育个体的转化率为α．

5)单位时间不育个体恢复率(即不育的一部分会变为可育的)为δ．

基于以上假设，建立不育控制下的单种群模型为

由于一些害鼠物种之间没有连续的重叠代，在(1)中令微分步长为1，利用欧拉法得到离散种群模型

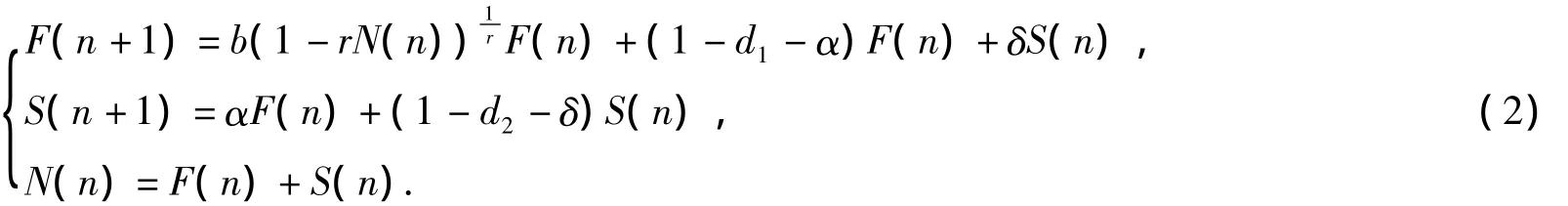
根据实际意义假设1－d1－α＞0，1－d2－δ＞0，(2)的初始函数满足 F(0)＞0，S(0)≥0．

2 平衡点的局部稳定性分析

定理1(i)当 R0=(d1(d2+δ)+d2α)/(b(d2+δ))＞1 时，(2)仅存在零平衡点 E0=(0，0);

(ii)当 R0=(d1(d2+δ)+d2α)/(b(d2+δ))＜1时，(2)除平衡点 E0外还存在正平衡点 E*(F*，S*)，其中，F*=((1－Δ)/r)·(d2+δ)/(d2+α+δ)，S*=((1－Δ)/r)·α/(d2+α+δ)，Δ =Rr0．

下面介绍差分方程平衡点稳定性的一般准则．

若某二维离散系统在其平衡点E处的线性化系统为X(m+1)=WX(m)，其中W为该差分系统在平衡点E处的Jacobi矩阵．若W特征值的绝对值都小于1，则平衡点E是局部渐近稳定的．即W同时满足3个Jury条件:(i)1－tr W+det W＞0;(ii)1+tr W+det W＞0;(iii)1－det W＞0．

定理2 当R0＞1时，(2)的平衡点E0=(0，0)是局部渐近稳定的．

证明 令 ψ=1－d1－α，μ=1－d2－δ．则(2)在E0=(0，0)处的Jacobi矩阵

由矩阵W0得tr W0=b+ψ+μ＞0，det W0=(b+ψ)μ－δα＞0．于是

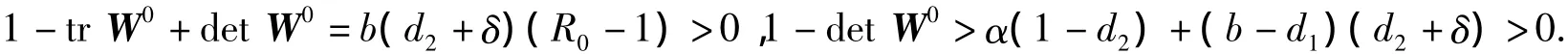
显然，1+tr W+det W＞0，从而满足3个Jury条件，因此平衡点E0是局部渐近稳定的．

定理3 当R0＜1时，(2)的正平衡点E*是局部渐近稳定的．

证明 (2)在E*处的Jacobi矩阵为

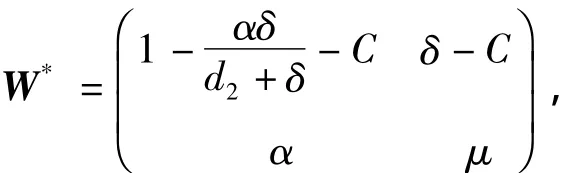
其中C=bF*=b(d2+δ)/(d2+δ+α)·R0·(1－R0－r)/(－r)．令 f(x)=(1－x－r)/(－r)，x＞d1/b．显然有 f'(x)= －x－r－1＜0．故当 x＞d1/b时，f(x)≤f(d1/b)=(1 －(d1/b)－r)/(－r)．令 g(t)=1 －(d1/b)t－t(t＞0)．从而 t＞0 时，g'(t)=ln(d1/b)(d1/b)t－1 ＜0，且有 g(0)=0．因此 g(t)＜0，即 g(t)=(1－(d1/b)t)/t＜1(t＞0)．由于(1－R0－r)/(－r)＜1，从而 C=(b(d2+δ)/(d2+δ+α))·R0·(1－R0－r)/(－r)＜(d1(d2+δ)+d2α)/(d2+δ+α)．根据矩阵W*得tr W*=1－αδ/(d2+δ)－C+μ，det W*=(1－αδ/(d+δ)－C)μ－δα+αC．由Jury条件可知，当(2)在正平衡点 E*处的 Jacobi矩阵 W*满足 tr W*＜1+

2det W*＜2时，正平衡点E*是局部渐近稳定的．而 tr W*=1－αδ/(d2+δ)－C+μ＞1－(d1(d2+δ)+d2α)/(d2+δ+α)－αδ/(d2+δ)＞0．因此只需证明 tr W*＜1+det W*＜2．因此1－tr W*+det W*=C(d2+δ)+αC ＞0，1－det W*=(d+δ)(1－C)+(1－α)C+αδ/(d+δ)＞0．故当R＜1时，tr W*＜1+det W*＜2．即

220

满足Jury的3个条件，所以正平衡点E*(F*，S*)是局部渐近稳定的．

3 主要结果

定理4 当R0＞1时，(2)的平衡点E0是全局渐近稳定的．

证明 因为 R0＞1，所以 b－d1＜αd2/(d2+δ)＜1．定义 Lypunov函数 V(F，S)=F(n)+S(n)．由(2)得

其中Θ=min{b－d1，d2}，显然0＜Θ＜1．从而平衡点E0是全局渐近稳定的．为证明(2)的解是持续生存的，引进引理1．考虑

其中 ω≥0，0＜d＜1 是正常数．则对(3)有引理1［8］．

引理1 令u(n)是方程(3)满足u(0)＞0的解．则

(a)nl→im∞u(n)=ω/d;(b)任给常数 ε ＞0，M ＞0，存在正常数δ(ε)(ε，M)使得当

定理5 当δ=0，R0＜1时，(2)的解是一致持续生存的．

证明 易证明(2)是耗散的．即存在常数M＞0，使得集合Ω={(F，S )0≤Fn≤M，0≤Sn≤M}为(2)的正向不变集．

考虑方程

令 v(n，n0，v0)为(4)的解．根据引理 1，对于 n0∈Z+，0≤v0≤M，给定 ε1＞0 和正常数 M，存在常数 δ0=δ0(ε1)＞0和 n*=n*(ε1，M)＞0 使得 e(n)＜ δ0，n≥n0+n*时，0≤v(n，n0，v0)＜ ε1．由本定理条件知，存在常数 η 和 ε1满足(1－((d1+α)/b)1r)/r＞ε1+η，αη ＜ δ0．即

下面证明存在常数β使得对于(2)的任意解有

首先证明(2)的任意解(F(n)，S(n))有

由解的有界性知对每个 m，存在 K使得当 n＞K时，F(n，θ)＜M，S(n，θ)＜M．又因为当 q→+∞时，s(qm)→+∞．所以存在K1(m)，使得q＞K1(m)时，s(qm)＞K(m)．令q≥K1(m)，故n∈［s(qm)+1，t(qm)－1］时，，从而可得

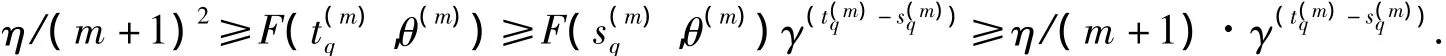
故当 q≥K1(m)，m=1，2，…时，t(qm)－s(qm)≥(ln(m+1))/(－ ln γ)．进而，可取，使得 m≥．q≥K1(m)时，有t(qm)－s(qm)≥n*．对任意的 m≥，q≥K1(m)及 n∈［s(qm)，t(qm)］，Sn+1≤α·η/(m+1)+(1 －d2－δ)Sn成立．设v(n)是(4)满足 v(s(qm))=S(s(qm))的解，则当 n∈［s(qm)，t(qm)］，m≥，q≥K1(m)时，有 S(n，θ(m))≤v(n)．取n0=s(qm)，v0=S(s(qm))，由于 0＜v0＜M，αη ＜ δ1，因此可得 n∈［s(qm)+n*，t(qm)］时，方程(4)的解 v(n，s(qm)，u(s(qm)))满足 v(n)=v(n，s(qm)，u(s(qm)))＜ ε1．故 S(n，θ(m))＜ ε1，n∈［s(qm)+n*，t(qm)］，q≥K1(m)，m≥．根据(2)的第一个方程和比较定理，可得当m≥，q≥K1(m)，n∈［s(qm)+n*，t(qm)］时，

成立．因此η/(m+1)2≥F(s(qm)，θ(m))≥F(s(

qm)－1，θ(m))(b(1 －rη －rε1)1r+1－d1－ α)＞ α0/(m+1)2．

这导致矛盾．因此，存在η＞0使得对于(2)任意的解(F(n)，S(n))，有 lnim inf F(n)＞η．类似可得，存在 η'，

→∞使得．从而定理得证．

4 结论

本文主要讨论了不育控制的作用．从定理4～5可以看出，当不育转化率α比较小，使得R0＞1时，(2)的解是持续生存的，且可以借助Matlab软件可得正平衡点是全局渐近稳定的;种群规模趋向于(1－((d1(d2+δ)+d2α)/(b(d2+δ)))r)/r．当α比较大，使得R0＜1时，种群逐渐消失．由定理4～5得，若不育者的恢复率δ比较小，使得R0＜1时，种群是灭绝的．若不育剂失效了，导致恢复率变大且使得R0＜1，从而种群将会持续生存．所以在对害鼠进行控制时，应使α比较大，而δ比较小．

［1］ 陈东平，王晓．鼠类不育技术控制鼠害的理论与实践［J］．预防医学情报杂志，2005，21(2):163－165．

［2］ 张涛，刘铭泉．不育剂在灭鼠中的应用研究［J］．中国媒介生物学及控制杂志，2005，16(4):327－328．

［3］ 宛新荣，石岩生，宝祥，等．不育剂对黑线毛足鼠种群繁殖的影响［J］．兽类学报，2006，26(4):392－397．

［4］ 张知彬．鼠类不育控制的生态学基础［J］．兽类学报，1995，15(3):229－234．

［5］ 刘汉武，周立，刘伟，等．利用不育技术防治高原鼠兔的理论模型［J］．生态学杂志，2008，27(7):1238－1243．

［6］ 郝丽杰，蒋贵荣，鹿鹏．具有垂直传染的SIRS传染病模型分岔分析［J］．郑州大学学报:理学版，2013，45(2):31－36．

［7］ 张美明，张凤琴，吕江，等．具有性别结构的免疫不育控制模型［J］．信阳师范学院学报:自然科学版，2011，24(4):425－429．

［8］ Xu Jiabo，Teng Zhidong．Permanence for nonautonomous discrete single-species system with delays and feedback control［J］．Applied Mathematics Letters，20140，23(9):949 －954．