钢管拱桁架结构抗震特性的变参数分析

琚婷婷，赵 峰，李茂新，万 凯

（1.武汉科技大学，武汉 430070；2.中冶南方技术有限公司，武汉 430080；3.中国建筑第八工程局有限公司广西分公司，南宁 530000）

钢管截面材料绕形心分布，回转半径大、抗扭能力强［1］，钢管桁架这种设计师青睐的钢结构形式也越来越多，但是对于这类型的结构设计并没有一套科学系统的指导前期的概念设计，鉴于此原因，该文采用振型分解反应谱法，并利用SAP2000有限元分析软件对钢管拱桁架在地震作用下的动力性能进行研究，得到各自的动力特性；该文首先分析关键参数对钢管拱桁架的自振频率的影响，然后对结构抗震性能进行变参数分析，得到各参数的取值范围。

1 模型的建立

基本模型结合了某原料厂的工程实例，取其中两榀钢管拱桁架结构为分析模型，单跨跨度L＝60m，结构的矢高F＝5.47m，结构采用倒三角的截面形式，截面宽度W＝3m，截面高度H＝3.5m，榀间距为15m，有横向支撑。杆件规格如下表1所示，与拱结构连接的钢柱高15m，采用H950X400X10X18，钢柱与地面刚接，与桁架铰接，钢材选用Q235钢；荷载的确定：考虑结构的自重、檩条、悬挂物等，结构由由永久荷载控制，不考虑风荷载，只考虑永久荷载和可变荷载的全跨组合，计算得到加到钢管桁架上弦每个节点的集中恒荷载为3.4kN，集中活荷载为3.8kN。

表1 杆件规格图

地震取值：8度设防烈度，0.2g，设计分组第二组，第Ⅱ类场地，结构的阻尼比为0.02［2］。桁架的计算中，在进行动力响应的分析中，采用振型分解反应谱进行计算，材料假定为线弹性。

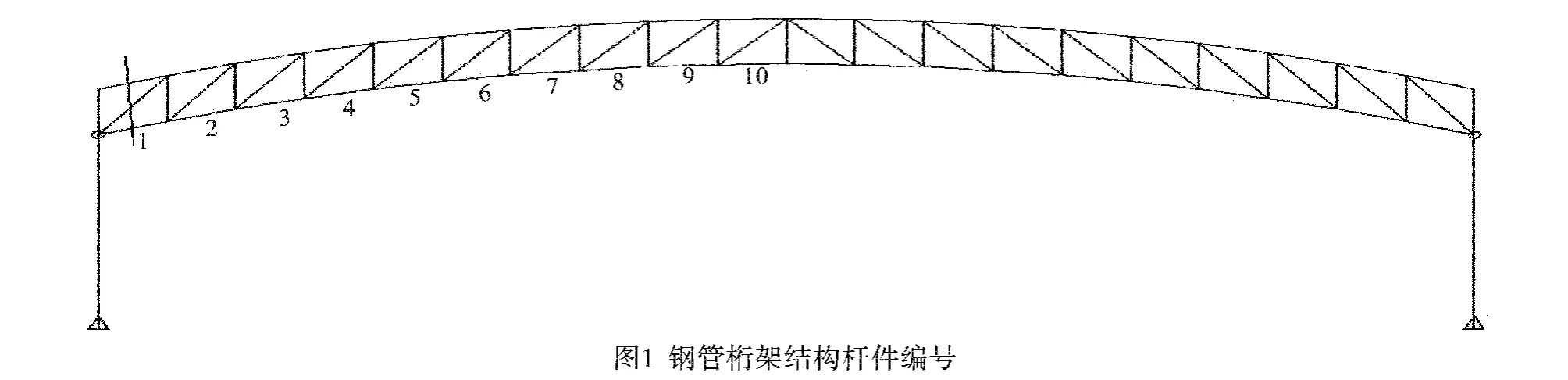
2 钢管拱桁架自振特性的变参数分析

根据文献［3］影响钢管桁架拱结构稳定性的显著因子为矢跨比、高跨比、宽高比。在结构的动力分析中，质量矩阵对结构的受力性能有重要影响，所以两榀桁架之间的间距也是影响结构动力响应的主要参数［4］。按照以上分析，本次研究假定四个主要参数：结构的矢跨比（F／L）、高跨比（H／L）、宽高比（W／H）以及榀间距（S）。分析单一参数变化下对此类非落地式钢管拱桁架结构自振特性的影响。4个基本参数的取值如表2所示。

表2 自振特性基本参数分析取值

通过基本模型的变榀间距、矢高、截面宽度和截面高度的方式分析结构的自振频率变化规律。图2～图5为各变参数对自振频率的影响曲线。

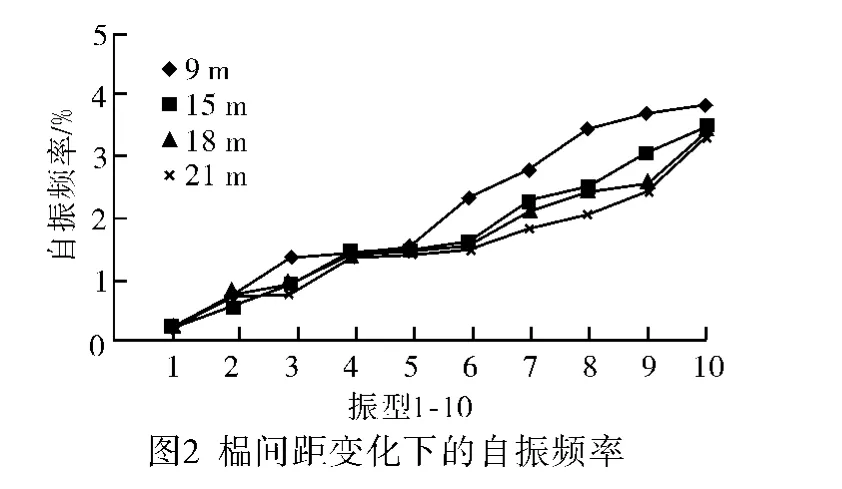
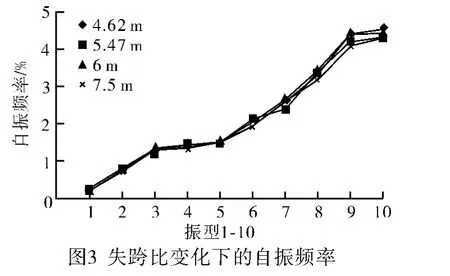
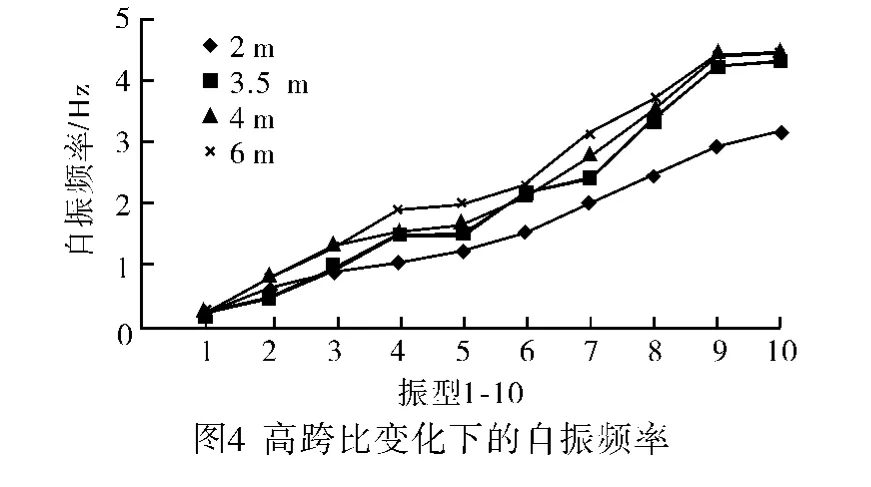
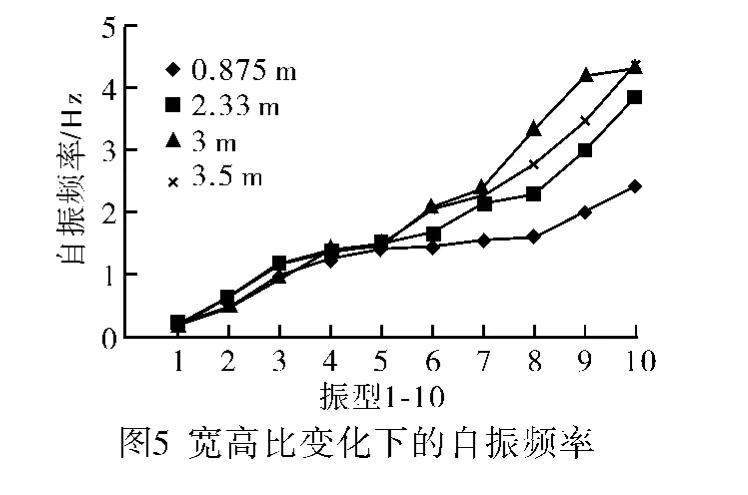
从上述变形曲线总结出以下观点：1）结构的榀间距较大时，自振频率较小；结构的榀间距较小时，自振频率较大；且在4阶，5阶，榀间距的变化对自振频率影响不大。2）结构矢高的变化对结构的自振特性影响不大。3）桁架的截面高度越高，自振频率越大。4）桁架的截面宽度越宽，自振频率越大；但在前5阶内，截面宽度的变化对自振频率的影响不大。

通过以上分析，可以得到以下结论：结构的榀间距、截面的高跨比和宽高比对钢管拱桁架结构的动力特性有一定的影响，结构的矢高比对钢管拱桁架结构的动力特性影响很小。

3 钢管拱桁架在变参数下的动力响应

由前面分析可知，榀间距、高跨比、宽高比对结构的动力特性影响显著，再由于拱结构矢高也是一个重要参数，因此将矢跨比、高跨比、宽高比和榀间距作为四个变参数对钢管拱桁架结构进行地震响应分析，这四个参数的取值如表3所示。

表3 地震响应基本参数取值

分析模型为理想对称结构，所以在取结构相同的一榀中的一半进行杆件轴力分析，杆件编号如图6所示。

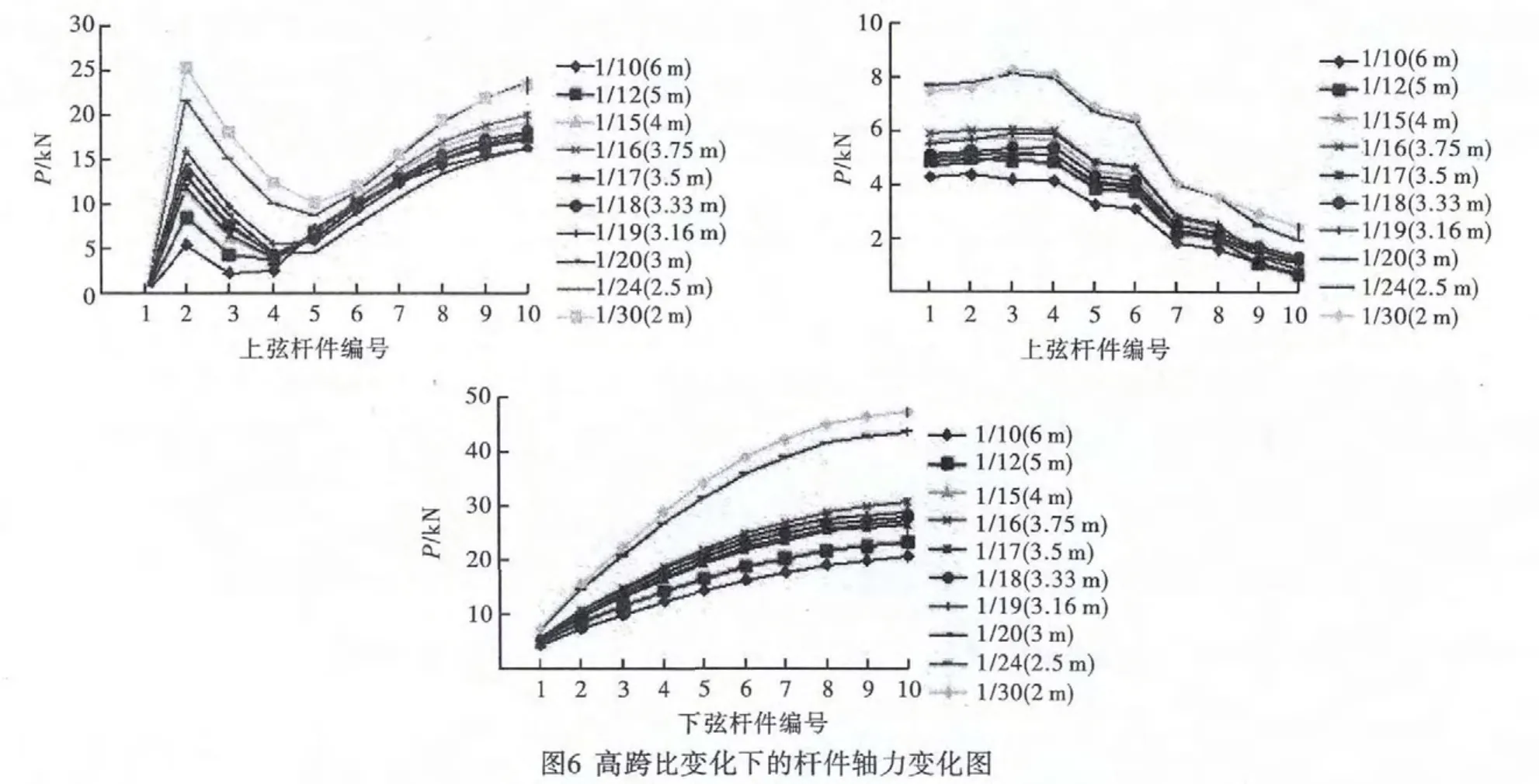
在此分析中，P代表水平地震产生的杆件轴力。

3.1 榀间距变化下的杆件轴力变化规律

根据上弦、下弦、腹杆在榀间距变化下得到不同的水平轴力，总结出杆件轴力的变化规律：1）随着榀间距的增大，上弦杆件的最大值也越来越大；上弦杆件的轴力最大值出现在上弦杆10，即跨中处。2）随着榀间距的增大，腹杆的最大值越来越小；腹杆的最大值出现在杆件4，距离拱端1／5。3）随着榀间距的增大，下弦杆件的最大值越来越小；下弦杆件的轴力最大值出现在下弦杆10，即跨中处。

3.2 高跨比变化下的杆件轴力变化规律

根据上弦、下弦、腹杆在高跨比变化下得到不同的水平轴力，整理出图6所示的变化规律，由此可以总结出：1）随着高跨比的增大，上弦杆件轴力最大值越来越小；当高跨比H／L≤1／19时，上弦杆的轴力最大值出现在上弦杆10，即跨中，且在上弦杆2出现与轴力最大值相差不到10%的较大值轴力；当高跨比H／L＞1／19时，上弦杆件轴力最大值就在杆件10，即跨中。2）随着高跨比的增大，腹杆轴力最大值越来越小；高跨比H／L≥1／15时，腹杆的轴力最大值出现在腹杆2；当H／L＜1／15时，腹杆轴力最大值出现在腹杆3。3）随着高跨比的增大，下弦杆件轴力最大值越来越小；且下弦杆件轴力最大值始终出现在下弦杆10，即跨中处。

3.3 宽高比变化下的杆件轴力变化规律

根据上弦、下弦、腹杆在截面宽高比变化下得到不同的水平轴力，整理出一定的变化规律，由此可以总结出：1）随着宽高比的增大，上弦杆件轴力最大值越来越小；当高跨比W／H≤1／2.5时，上弦杆的轴力最大值出现在上弦杆2，即离杆端1／5处；当高跨比W／H＞1／2.5时，上弦杆杆件轴力最大值就在杆件10，即跨中。2）宽高比W／H≤1／1.4时，腹杆的轴力最大值出现在腹杆4；当W／H＞1／1.4时，其中W／H＝1／1.3腹杆轴力最大值出现在腹杆1，其他情况轴力最大值大都集中在杆2或杆3。3）随着宽高比改变，下弦杆件轴力最大值一直出现在下弦杆10，即跨中处。且当宽高比W／H≤1／1.4，下弦杆件轴力最大值越来越大；当W／H＞1／1.4时，下弦杆件轴力最大值越来越小。

3.4 矢跨比变化下的杆件轴力变化规律

根据上弦、下弦、腹杆在矢跨比变化下得到不同的水平轴力，整理出一定的变化规律，由此可以总结出：1）随着矢跨比的改变，上弦杆件轴力最大值一直出现在下弦杆10，即跨中处。当矢跨比F／L≥1／12时，随着矢跨比的增大，上弦杆件的轴力最大值越来越小；且在F／L＜1／12时，随着矢跨比的增大，上弦杆件的轴力最大值越来越大。2）随着矢跨比的增加，腹杆的最大值越来越大，腹杆的最大值出现在杆件2，距离拱端1／5。3）随着矢跨比的增加，下弦杆件的最大值越来越大，下弦杆件的最大值出现在杆件10，即跨中处。

3.5 取值范围分析

根据上节图表可知，高跨比的下弦杆轴力最大值起主要控制作用，当H／L＝1／30时，其值为Pmax＝47.38kN，所以在进行设计时在允许误差15%的范围里，1／30×（1－15%）＝1／25，其最大值为40.1kN，则把高跨比控制在1／25≤H／L≤1／10范围内；当Pmax≤40.1kN时，宽高比W／H≥1／3，所以宽高比最好控制在1／3≤W／H≤1；当Pmax≤40.1kN时，矢跨比W／H≤1／9，所以矢跨比最好控制在1／9以内；当Pmax≤40.1kN时，榀间距S＞9m，所以榀间距最好控制在9m以外。

4 结 论

a.影响钢管拱桁架结构自振特性的影响因素有结构的榀间距、矢跨比，截面的高跨比、宽高比；其中影响因素较大的是截面的高跨比和宽高比。

b.钢管拱桁架在榀间距、矢跨比、高跨比和宽高比的变化下呈现一定的变化规律，结构的高跨比对结构动力响应影响较明显，且分析得到在进行此类结构设计时，高跨比控制在1／25到1／10内；宽高比控制在1／3到1范围内；矢跨比控制在1／9以内；榀间距控制在9m以外，这四个参数在此范围内是比较合理的，分析结果为此类结构的概念性设计提供参考。

c.此钢管拱桁架结构的分析模型没有考虑柱子刚度对地震特性的影响，该论文对这方面的研究还比较匮乏，还需要进一步研究分析。

［1］吴连杰，张 勇.大跨度钢管结构的研究与应用［J］.钢结构，2006（增刊）：42－48.

［2］GB 50011—2010建筑抗震设计规范［S］.

［3］王丹丹.空间钢管桁架结构动力性能及抗震方法研究［D］.兰州：兰州理工大学，2012.

［4］王丽娜.空间钢管桁架结构动力性能及抗震方法研究（1）［D］.北京：北京交通大学，2008.