桥梁荷载横向分布系数研究

韩劲龙，郝艳广，刘相良

（1.中交武汉港湾工程设计研究院有限公司，武汉 430040；2.武汉港湾工程质量检测有限公司，武汉 430040）

随着有限元理论和大型有限元软件技术的发展与普及，采用有限元模型对结构进行空间分析得以实现。对于采用横隔板，桥面板或其他连接方式将T梁横向连接成一整体的梁桥，通过桥面板、横隔板将T梁横向连接在一起的梁桥，当荷载P作用于桥面时，由于桥面横向刚性的存在，荷载在横纵方向传递，使桥梁结构整体受力，结构受力与变形成空间分布，故采用空间计算理论对此问题进行分析更接近工程实际。桥梁前辈们把空间问题转化为平面问题，使桥梁横向分布系数手算变的便捷，但对于复杂的大跨度桥梁忽略某些空间问题，会造成计算的偏差变大，对桥梁设计不利，因此通过大型有限元软件进行空间计算横向分布系数更符合实际。

1 比拟正交异性板法

传统的荷载横向分布系数计算方法，是通过将T梁桥假设为一并排放置的主梁，并通过梁格或梁系的结构将其横向联系成一整体，通过相应假设对其进行力学分析。不同之处，在于不同桥梁跨径与跨度，横向连接刚性假设不同。根据桥梁跨度与跨径的特性，对于由常见公路T梁桥，当宽跨比较大时，一般可将其假设为矩形的平板，按弹性薄板对其进行力学分析，此法业内称为“比拟正交异性板法”，它采用的是古典弹性力学分析方法，具体分析方法见文献［1］。

2 有限元分析法

有限元分析法是一种数值分析方法，大型有限元软件中根据结构构件受力的不同，建立不同的单元形式，如：梁单元、壳单元、索单元、实体单元等，该文的分析对象主要为梁单元。梁单元的受力为：不仅承担拉压力，还承受剪力弯矩，而且空间梁单元每个节点均有6个自由度，分别为3个转动和3个平动。根据荷载作用下横截面受力，分自由扭转与翘曲扭转。翘曲扭转考虑截面双力矩和翘曲扭矩两项内力的作用。用空间梁单元进行离散分析，可直接计算内力和变形。

3 计算实例

3.1 概况

一座特大桥，上部构造布置为5×40预应力混凝土T梁结构，其横截面如图1所示，计算跨径39.7m，两端桥墩设GYZD25×75mm。混凝土标号为C50。

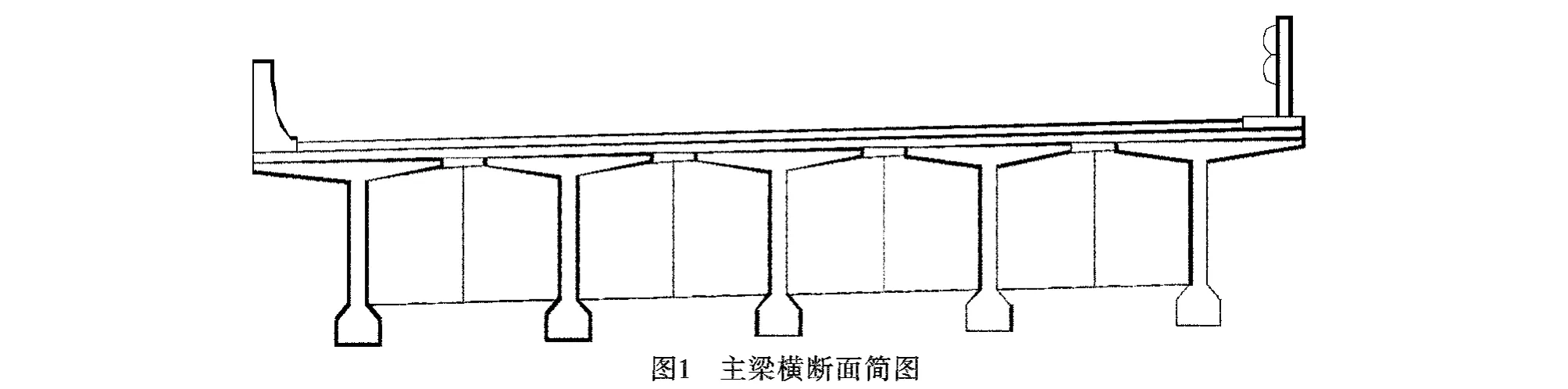
3.2 计算模型

采用通用大型有限元软件MIDAS／Civil建立T梁模型。有限元模型如图2所示。

3.3 计算方法

在桥梁横向受力特性计算中，荷载横向分布系数是为描述桥梁横向受力特性而提出的概念，其实质是“内力”横向分布，而不是荷载的横向分布，即荷载作用下，该横截面中各梁的受力大小，由文献［2］可知，每片T梁的横向分布由下式求得

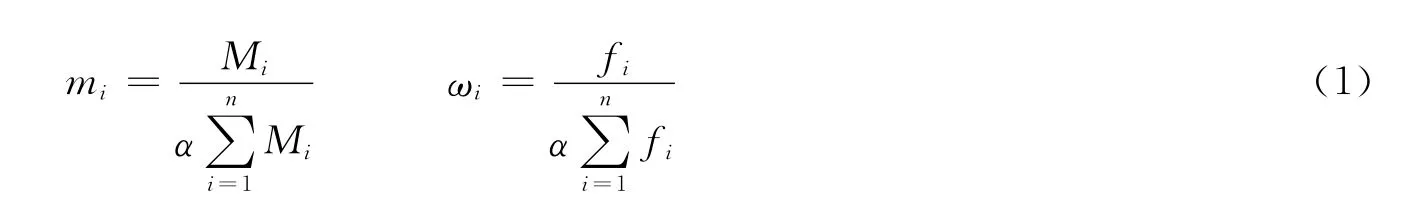
式中，Mi为荷载作用下，某一量测截面第i片梁的弯矩；ωi为荷载作用下，某一量测截面第i片梁的挠度；α为荷载系数，汽车取1／2，挂车取1／4，人群取1。

3.4 计算结果

40m T梁弯矩的计算云图如图3，挠度的计算云图如图4所示。

采用有限元软件以跨径40m、30m、20m、15m为例，通过T梁的受力和挠度，分别计算得各主梁的横向分布系数，并与文献［1］的方法（比拟正交异性板）计算结果对比，计算结果如表1所示。

表1 横向分布系数对比表

由表1可知，不同跨径的T梁的横向分布系数有限元模型根据挠度的计算值和理论计算值的相对误差百分比，随着跨径的增大而增大。因为随着跨径的增大，桥梁的空间特性更加明显，不确定因素也增加。

4 结 语

通过MIDAS建立空间桥梁结构，计算不同跨径的T梁横向分布系数与比拟正交异性板法计算值相对比，得出在桥梁设计中，当T梁跨径小于30m时可采用理论简化计算方法进行荷载横向分布计算，当跨径大于30m时，荷载横向分布系数的计算要通过有限元软件建立空间计算模型来实现，可以为工程设计提供参考。

［1］范立础.桥梁工程（上）［M］.北京：人民交通出版社，1986.

［2］李国豪 ，石 洞.公路桥梁荷载横向分布计算［M］.北京：人民交通出版社，1987.

［3］谭毅平.大跨度刚架拱桥的荷载横向分布研究 ［J］.建筑结构，2003（7）：118－120.

［4］张洪俊.SAP2000桥梁结构分析应用方法与实例［M］.北京：人民交通出版社，2005.