基于神经网络电性源半航空视电阻率反演研究

嵇艳鞠 徐 江 吴 琼 王 远 冯 雪栾 卉 关珊珊 林 君

（1.吉林大学仪器科学与电气工程学院，吉林 长春130026；2.国土资源部地球探测技术及仪器重点实验室，吉林 长春130026）

引 言

时域半航空电磁系统，融合了地面时域电磁系统和航空电磁系统的优势，具有探测深度大、分辨率高、范围广、速度快等优点［1］，尤其适合在深林覆盖区、沼泽、海陆交互带等人难以到达的恶劣地形环境中开展快速勘探工作.

国内外，在半航空电磁探测系统和数据解释方法方面开展的研究较少.虽然早在1998年，Tohru Mogi提出了电性源半航空电磁探测方法，但是该方法发展缓慢，直至2009年，Tohru Mogi将半航空电磁探测系统（Grounded Electrical-source Airborne Transient Electromagnetic，GREATEM）用于日本东北部盘梯山的火山地质结构调查，并取得了较好效果［2-4］.在2013年，Sabry Abd Allah利用GREATEM系统，在日本东南部的沿海地区，进行了海陆交汇区域地下500m的地下电阻率结构探测，并查明海水入侵的趋势［5］.在国内，2009年，嵇艳鞠等开展了大定源时域半航空电磁理论响应研究［6］，并在2012年研究了基于地面（Long Offset Transient Electromagnetic Method，LOTEM）的半航空电阻率计算方法（文中简称传统方法）［7］.2013年王远等采用自主研制的基于飞艇的电磁探测系统，在江苏省如东县岔河镇和马塘镇的龙凤村开展了飞行探测，探测结果清晰地反映了咸淡水变化趋势和咸水侵入方向，与当地的地质水文资料一致［8］.

目前，半航空电磁探测数据处理和解释主要采用地面LOTEM方法，忽略接收高度的影响.这种近似等效导致计算的电阻率与真实电阻率偏差较大，尤其在源附近，计算偏差更大.为了准确获得地下结构的电阻率值，需要研究新的电阻率反演方法.人工神经网络能够避开复杂的数值计算，高精度地拟合非线性关系.在具有不确定性和非结构性的电磁探测信号处理方面有明显优势.2010年朱凯光基于假层半空间模型，将人工神经网络方法用于航空电导率成像［9］，提高了电阻率反演解释精度；2012年J.L.Gunnink在航空电磁数据反演时，采用人工神经网络成功地识别了高导围岩中的冰碛物层识别［10］.

神经网络反演方法在航空电磁系统电阻率反演方面得到了较好的应用.但是半航空电磁探测系统的实测衰减曲线随不同收发距变化，其曲线形态和极性变化复杂［11］，不能直接利用航空电磁数据反演方法.为此，提出基于时域半航空电磁理论的快速正演方法，利用矩阵运算的优势，完成时域半航空快速高效的正演计算，形成正演样本集.对样本集进行等效变换，建立误差反向算法（Back Propagation，BP）神经网络，通过对样本集数据的训练、验证、测试、仿真，形成针对电性源时域半航空数据反演的神经网络，并对视电阻率-深度反演成像.

1 电性源时域半航空电磁响应理论分析

1.1 电性源时域长导线源响应计算

电性源时域半航空系统，采用2～3km的接地长导线源作为发射，将接收系统和接收线圈固定在直升机或飞艇上进行接收.长接地导线源在层状大地下的感应电动势垂直分量表达式为［12］

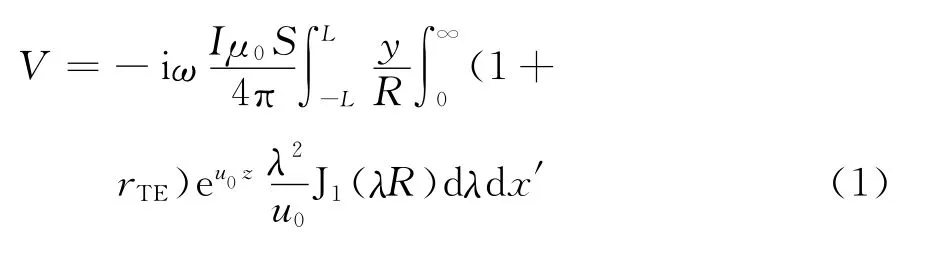
式中：Ⅰ为发射电流；J1为贝塞尔函数；y为观测点的y坐标；λ为积分变量；自然对数的底e＝2.718 28；rTE为反射系数；S为接收线圈的有效面积；μ0是空气的磁导率.

在数值计算过程中，式（1）中含有一阶贝塞尔函数的内层积分和外层积分，传统的数值迭代方法用Hankel数值积分变换算法解决内层积分［13］，Gauss数值积分解决外层积分，运算速度慢，计算单点响应值需要627.7s，计算效率不适于建立海量神经网络样本集数据.

基于矩阵运算的思想，将Hankel和Gauss数值积分中变量相乘项用矩阵相乘来实现，避免了大量的循环计算，单点响应值计算时间平均不到0.01 s.计算速度是传统数值迭代方法的7 000多倍，极大地缩短了计算时间，提高了正演计算的效率.然后，利用Guptasarma数值线性滤波法将得到的频率域响应Hz转换到时间域［14］，为数据反演奠定基础.

1.2 半航空电磁响应特征分析

根据吉林大学自行研制的电性源时间域半航空电磁系统的技术指标，具体参数如表1所示.计算了三层层状模型的电磁响应，层状模型电阻率、层厚度参数如表2，分别讨论了半航空电磁响应与飞行高度、电导率的关系.

表1 电性源半航空电磁系统工作参数

表2 三层H型层状大地模型参数

当接收高度为0m和30m、采样时间为0.2ms和5ms时，不同收发距的感应电动势值的包络曲线如图1所示.图1（a）为感应电动势早期0.2ms时的曲线，图1（b）为感应电动势晚期5ms时的曲线.

由图1可见，半航空感应电动势与地面感应电动势在早晚期的变化趋势不一致.收发距较小时的半航空感应电动势与地面感应电动势相差很大，达到100%以上，当收发距增大到一定程度时，半航空感应电动势与地面感应电动势差别变小，但仍达到30%左右.这一特征表明，半航空电磁信号与地面LOTEM电磁信号随时间和收发距的变化规律有很大区别［15］.地面长偏移距瞬变电磁方法并不适用于半航空电磁数据的解释.

图2给出了不同接收高度的层状模型在0.01～10ms范围的感应电动势曲线.可见，感应电动势在早期受接收高度的影响较大，高度每变化10m，幅值变化约为10%，不同高度的半航空感应电动势反演视电阻率的结果有较大的差异.所以，接收高度是进行电阻率反演时应该考虑的参数之一［16］.

图3给出了接收高度为30m时，不同取样时间的均匀半空间模型电阻率与感应电动势关系曲线.从图3中可见，在某一取样时间道，感应电动势和电阻率的对应关系具有二值性特征，直接采用感应电动势值无法确定唯一的电阻率值，给反演工作带来困难.

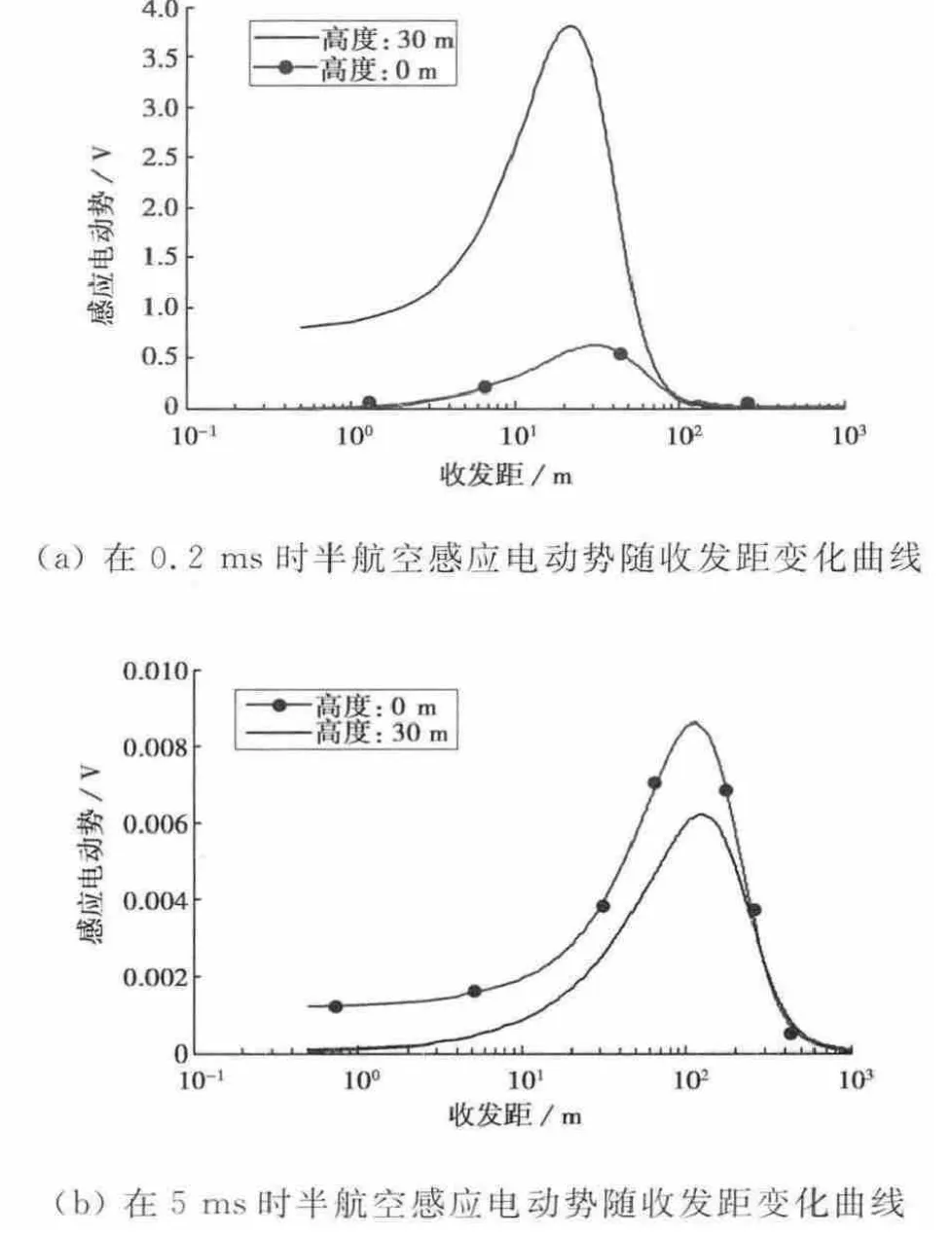
图1 不同收发距半航空电磁仿真信号变化规律

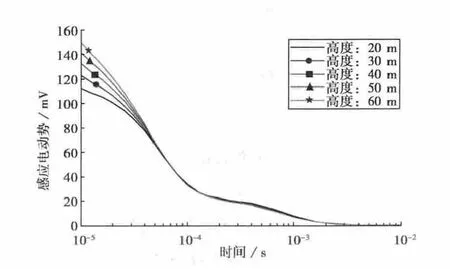
图2 层状地模型在不同接收高度的感应电动势曲线

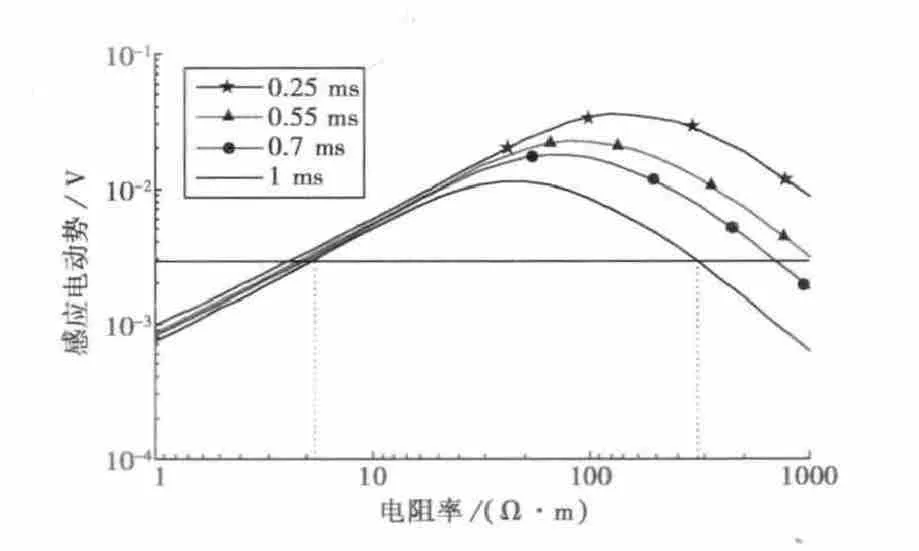
图3 均匀半空间模型的感应电动势曲线

通过分析半航空电磁响应特征，在电阻率反演时，需要考虑接收高度、收发距、感应电动势与电阻率的二值性等因素，需寻求新的反演方法.

2 BP神经网络理论

BP神经网络是一种按误差逆传播算法训练的多层前馈网络.通过误差反向传播来不断调整网络的权值和阈值，能够以任意精度逼近任意非线性关系，收敛速度快.以三层BP神经网络为例，结构如图4所示.

BP神经网络包括输入层、隐含层（中间层）和输出层.相邻各层神经元之间由权重系数相互连接，输入信号经过传递函数的作用由输入层传播到隐含层，再由隐含层传播到输出层，最后得到输出结果［17］，完成一次训练.

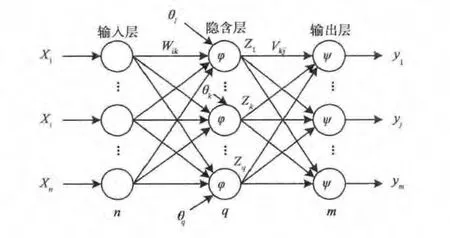
图4 三层BP神经网络结构示意图

在训练过程中，目标函数E为

式中：ti为第i个神经元的期望输出；yi为第i个神经元的实际输出；m为输出层神经元个数.

当E满足目标值时，实际输出和期望输出达到一致，网络训练结束.BP神经网络的训练过程如图5所示.

将训练样本集分为三部分：训练样本、验证样本、测试样本.将训练样本数据由输入层输入BP神经网络，经各层的权值和传递函数作用，由输出层输出.计算输出误差E（n），当E（n）小于目标误差值ζ时，结束训练，否则将E（n）反向传递，计算误差函数的梯度δ，依据δ调整每层的权值，重新训练网络.直到网络性能满足要求.同时利用验证样本对网络训练误差进行验证，若训练误差连续增大，则网络性能无法提高，应结束网络训练.训练完毕的网络，即可预测其它模型，达到反演的目的.

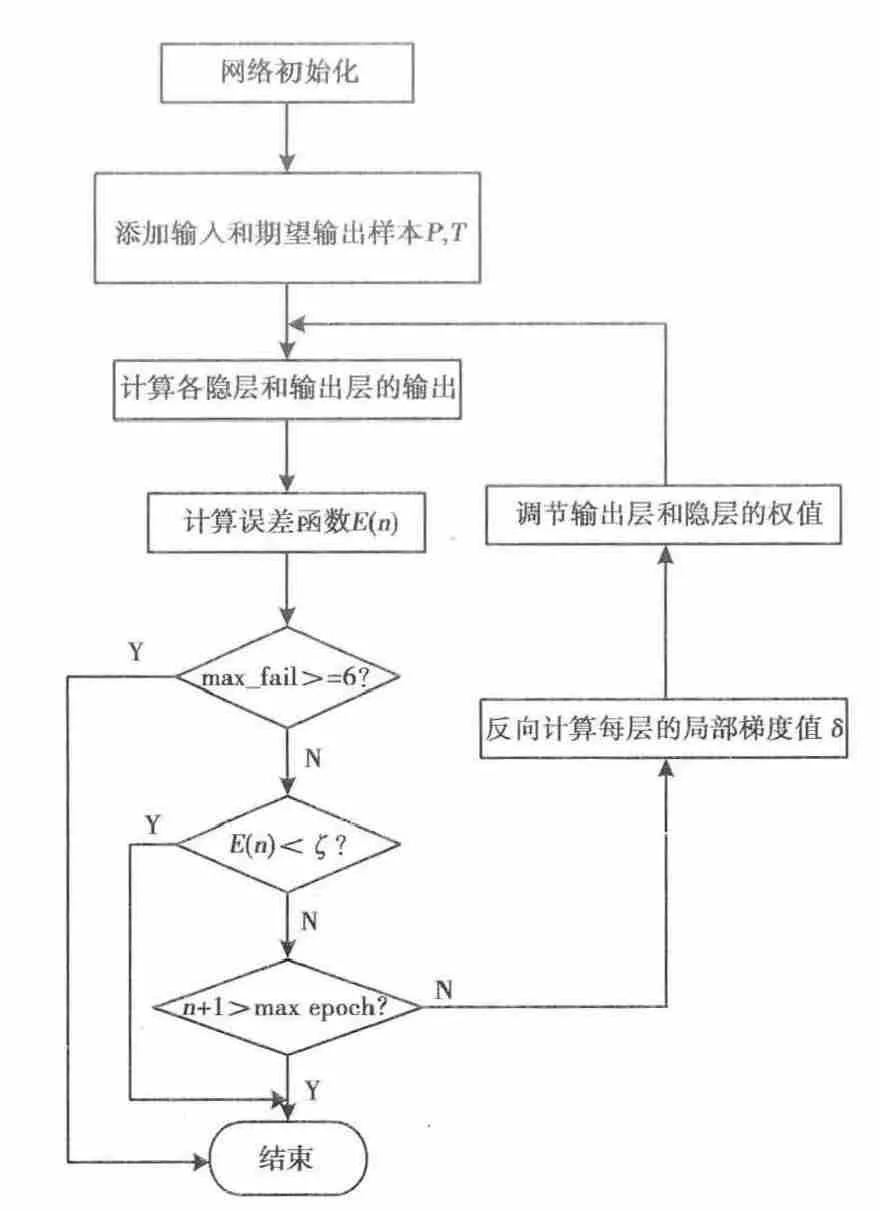
图5 BP神经网络训练流程图

3 时域半航空视电阻率反演方法

3.1 建立感应电动势与电阻率单一映射

由于视电阻率值和感应电动势之间是隐函数关系，且对应关系非唯一，是典型的非线性不适定问题.为了建立感应电动势与电阻率单一映射关系，将感应电动势在任意两个时间道进行变换，获得时间常数τi和响应幅值αi两个参数［18］.变换后，由一对τi和αi就可以唯一确定一个视电阻率值，从而解决了由感应电动势反演视电阻率值带来的非线性不适定问题.

时间常数τi和响应幅值αi的变换表达式为

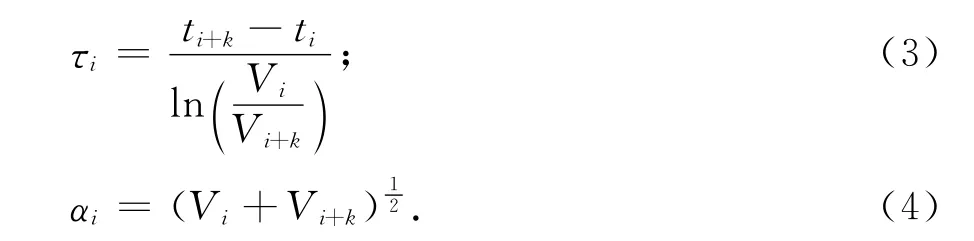
式中：ti为第i道的中心时间；Vi为第i道的感应电动势；k为时间道差.

根据公式（1）先对电阻率计算的半航空感应电动势衰减曲线进行取样处理，再利用公式（3）和（4）进行变换得到τi和αi，最终形成21个时间道的样本集.这样，建立了时间常数τi、响应幅值αi与某接收高度hi的电阻率值ρi一一映射关系.将τi和αi作为BP网络的输入，hi和ρi作为网络输出.若时间道差k＝1，则21道数据可以创建20个BP神经网络分别对20个样本集进行训练，其中，70%的样本集数据作为正常训练数据，15%的样本集数据作为验证数据，15%的样本集数据作为测试数据.

3.2 样本集网络训练

在对BP神经网络进行训练前，需对样本集数据进行预处理，主要对数据进行归一化处理和数据顺序打乱.经过归一化处理，使得样本数据的分布相对合理集中，加快网络训练收敛速度.数据顺序打乱后，将减小样本间数据相关性，提高BP网络的泛化能力.

将输入样本αi和输出样本ρi取对数后，归一化到0.1～0.9之间，将τi和hi直接线性归一到0.1～0.9之间.归一化到0.1～0.9，同时可以避免在后期利用神经网络进行预测时，输出结果反归一化后与真实结果间误差过大的现象.

经过预处理和网络参数设置后，即可进行网络训练.训练函数直接影响网络训练误差的大小，为提高网络训练的效率，选取几种常用训练函数对样本集进行训练，并比较这几种函数的训练误差，确定最优训练函数.表3给出几种训练函数的训练误差.从表3中可见，不同函数的训练误差相差较大，其中Levenberg-Marquardt（LM）法的训练效果明显优于其他算法.因此，选用LM算法对BP网络进行训练.当网络均方误差（Mean Squared Error，MSE）性能小于10-5时，认为网络性能达到要求.

在训练网络的过程中，每训练一次网络，将验证样本数据输入当前网络进行误差验证，当误差不再减小时，则停止训练.防止网络训练“过拟合”.当测试样本反演精度在5%以内，认为网络训练成功，最终确立了适用于半航空电阻率反演的BP神经网络.再根据趋肤深度公式计算深度参数，即可实现电阻率-深度成像.

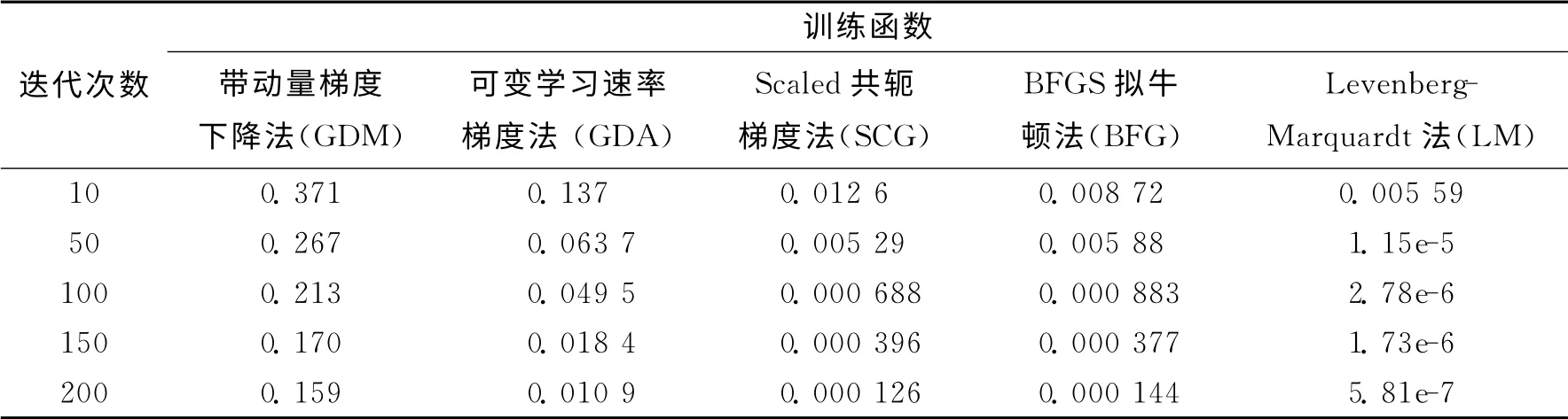
表3 不同训练函数的训练误差

4 理论模型测试结果分析

利用BP神经网络算法，分别对均匀半空间模型和层状大地模型进行反演，并与传统数值计算方法（参考文献［6］）结果对比，进而验证BP神经网络的正确性和有效性.

4.1 均匀半空间模型测试

对电阻率为100Ω·m的均匀半空间模型，分别采用引言中提到的传统方法和BP神经网络进行反演，反演结果如图6所示.从图中清晰可见，采用传统方法计算电阻率值，与真实电阻率值偏差比较大，尤其在浅部的视电阻率计算结果与真实模型的相对误差达到了60%以上，不同深度的平均误差达到20%以上.而采用BP神经网络反演结果与真实的电阻率值非常接近，最大相对误差小于5%，完全满足野外探测需求.

4.2 层状模型测试

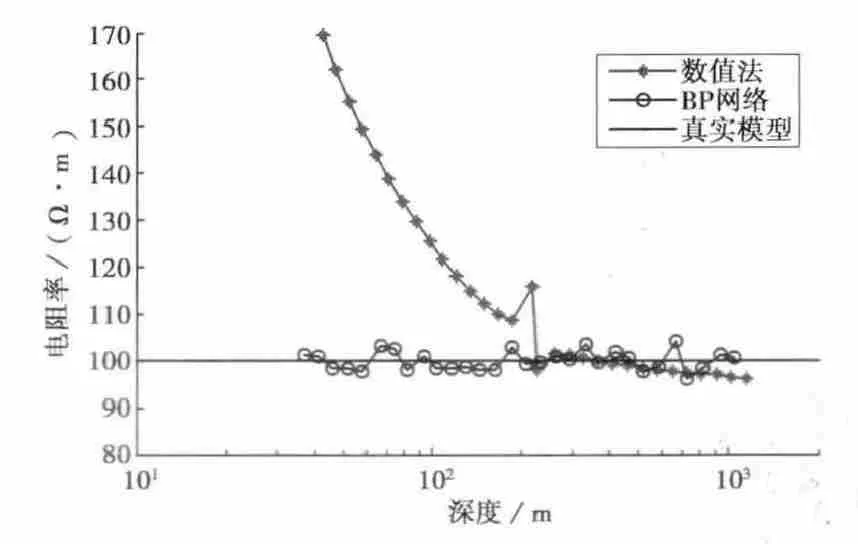
图6 均匀半空间模型视电阻率计算结果

为评价神经网络对层状模型的反演效果，设计了H型和K型层状大地模型，H型层状模型参数同表2一致，K型层状模型参数见表4，分别利用传统方法和BP神经网络算法进行反演.图7和图8为H型和K型模型反演结果.

表4 K型层状大地模型参数

从图7中可见，神经网络反演方法对低阻层的逼近程度、电性结构变化反映明显优于传统方法.在深度为20m的浅层高阻区，神经网络反演结果相对误差约为6.5%，而传统方法在此深度的电阻率信息丢失.对于深度为100～150m的低阻层和150 m以下的高阻区，神经网络反演结果相对于传统方法更加接近真实模型.

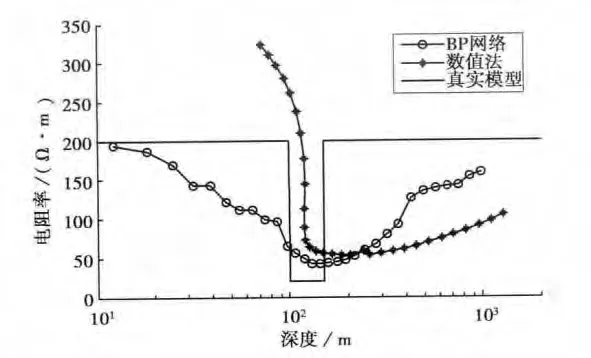
图7 H模型视电阻率反演结果

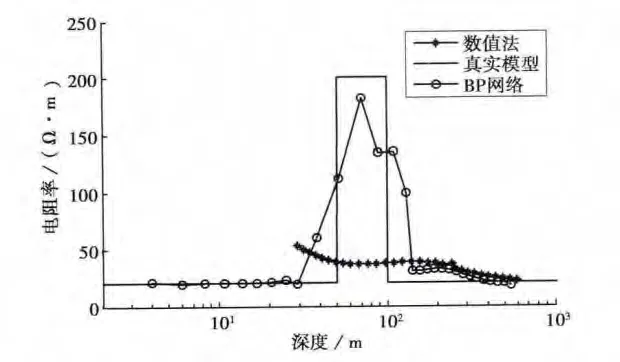
图8 K模型视电阻率反演结果

图8中可见，传统方法和BP神经网络反演在深度100m以后的结果基本一致.对于0～50m的低阻覆盖层，BP神经网络反演结果与真实模型非常接近，而传统方法在对应深度的电阻率信息大部分丢失.50～100m处的高阻层，BP神经网络反演结果也明显优于传统方法.

模型测试结果显示，传统方法在浅部反演误差较大，对深部的反演误差较小.这是由于传统反演方法将半航空数据直接等效为地面数据，利用地面数据反演方法进行反演.由上文半航空正演响应特征分析可知，地面数据在对应浅部信息的早期与半航空数据相差较大，导致反演结果误差大；随着采样时间的增大，地面数据和半航空数据之间的误差逐渐减小.反演误差随之减小.BP神经网络反演方法是基于半航空数据进行建立样本集、训练、反演的，所以反演精度较传统反演方法高.

神经网络反演精度在很大程度上取决于训练样本集的选取和网络结构的设定.神经网络算法对深部高阻层的逼近效果没有浅层好，一方面由于神经网络训练的样本集是基于均匀半空间模型的电磁响应；另一方面，对于电性结构变化的层状模型，其感应电动势曲线上存在着过渡过程［19］，因此，导致采用神经网络反演时过渡区域偏大，分辨率降低.

4.3 准二维大地模型

为了进一步检验神经网络反演的有效性，选择了H型模型的理论计算感应电动势作为仿真数据，围岩电阻率为200Ω·m，低阻层电阻率为20 Ω·m，低阻层埋深由-200m到-40m连续变化，如表5所示.

分别利用传统算法和BP神经网络反演算法得到视电阻率-深度断面图，反演结果如图9所示.

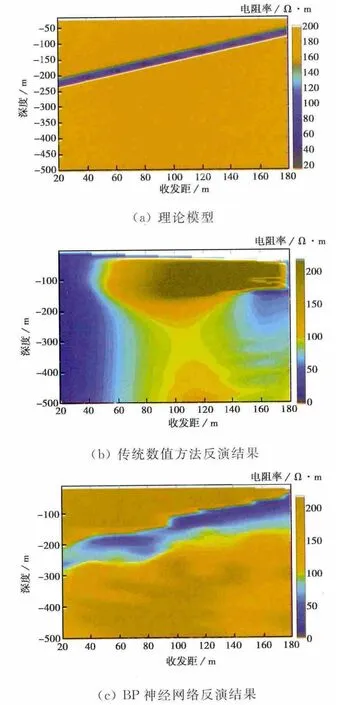
图9 三层大地模型视电阻率断面图

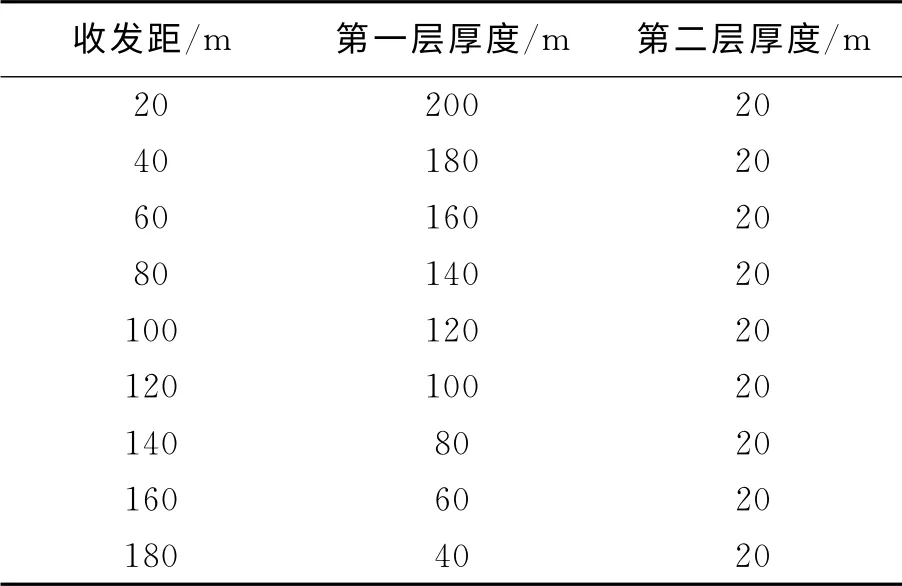
表5 三层模型埋深参数

图9（a）为理论模型示意图，图9（b）为传统方法计算成图结果，图9（c）为BP神经网络反演成图结果.从图9（b）中可以看出，收发距小于80m时的电阻率断面图与已知模型完全不吻合，呈低阻状态；当收发距大于100m时，从图中仅能分辨出存在低阻层，而无法显示出低阻层的厚度以及在深度上的变化趋势.从图9（c）中，则清晰地反映了低阻层变化趋势和厚度，与已知大地模型基本一致.

5 结 论

针对半航空瞬变电磁数据解释问题，基于BP神经网络，提出了半航空瞬变电磁视电阻率反演方法.主要结论如下：

1）通过对比分析半航空和地面电磁响应特征，讨论了收发距对感应电动势的影响，证明收发距大于5倍接收高度时，地面LOTEM方法反演半航空电磁数据结果有效.

2）在构建长导线源电磁响应样本集基础上，将理论计算的电磁响应进行等效变换，建立电磁响应与电阻率单一映射关系，解决了非线性不适定问题，通过利用BP神经网络对半航空电磁响应进行电阻率反演，提高了反演效率和精确度.

3）通过对层状模型和准二维模型的反演测试，表明BP神经网络反演方法能够清晰地反映地下电性结构变化和分辨低阻层.

全文以均匀半空间模型为基础，采用BP神经网络实现了半航空电磁数据电阻率反演，能够高效、准确地反映地下电性结构，适用于半航空瞬变电磁数据的快速反演.但本方法对于低阻层向高阻层变化趋势，分辨率还需要提高，可以通过增加样本数据、选取更合适的训练样本数据和训练方式；还需进一步研究BP神经网络反演方法，用于实测数据的处理.

［1］FOUNTAIN D.60years of airborne EM-focus on the last decade［C］／／5th International Conference on Airborne Electromagnetics.Haikko Manor，2008：1-5.

［2］MOGI T，TANAKA Y，KUSUNOKI K，et al.Development of grounded electrical source airborne transient EM（GREATEM）［J］.Exploration Geophysics，1998，29：61-64.

［3］MOGI T，KUSUNOKI K，KAIEDA H，et al.Grounded electrical-source airborne transient electromagnetic（GREATEM）survey of Mount Bandai，north-eartern Japan［J］.Exploration Geophysics，2009，40：1-7.

［4］ITO H，MOGI T，JOMORI A，et al.Further investigations of underground resistivity structures in coastal areas using grounded-source airborne electromagnetics［J］.Earth，Planets and Space，2011，63：9-12.

［5］ABD ALLAH S，MOGI T，ITO H，et al.Three-dimensional resistivity modeling of grounded electricalsource airborne transient electromagnetic（GREATEM）survey data from the Nojima Fault，Awaji Island，south-east Japan［J］.Exploration Geophysics，2013.

［6］嵇艳鞠，林 君，许洋铖.大定源时间域吊舱式半航空电磁勘探理论研究［C］／／第九届中国国际地球电磁学术讨论会论文集，2009：121-126.

［7］JI Yanju，YANG Guihong，GUAN Shanshan，et al.Interpretation research on electrical source of time domain ground-airborne electromagnetic data［C］／／World Automation Congress（WAC），24-28June，2012：1-4.

［8］WANG Yuan，JI Yanju，LI Suyi，et al.A waveletbased baseline drift correction method for grounded electrical source airborne transient electromagnetic signals［J］.Exploration Geophysics，2013.

［9］ZHU Kaiguang，MA Mingyao，CHE Hongwei，et al.PC-based artificial neural network inversion for airborne time-domain electromagnetic data［J］.Applied Geophysics，2012，9（1）：1-8.

［10］GUNNINK J L，BOSCH J H A.，SIEMON B，et al.Combining ground-based and airborne EM through Artificial Neural Networks for modeling glacial till under saline groundwater conditions［J］.Hydrol Earth Syst Sci，2012，16：3061-3074.

［11］嵇艳鞠，林 君，王 忠，等.浅层瞬变电磁法中全程瞬变场的畸变研究［J］.电波科学学报，2007，22（2）：316-320.JI Yanju，LIN Jun，WANG Zhong，et al.Analysis of distortion in all-time transient electromagnetic field based on inducing of ramp switch-off current for shallow survey［J］.Chinese Journal of Radio Science，2007，22（2）：316-320.（in Chinese）

［12］NABIGHIAN M N.Electromagnetic Methods in Applied Geophysics［M］.1988.

［13］GUPTASARMA D，SINGH B.New digital linear filters for Hankel J0and J1transforms［J］.Geophysics Prospecting，1997，45（5）：745-762.

［14］GUPTASARMA D，SINGH B.Computation of the time-domain response of a polarizable ground［J］.Geophysics，1982，47（11）：953-963.

［15］关珊珊，林 君，嵇艳鞠，等.激励信号对地-空瞬变电磁响应的影响分析［J］.电波科学学报，2012，27（4）：766-772.GUAN Shanshan，LIN Jun，JI Yanju，et al.Analysis of eacitation signal effect on grounded electricalsource airborn transient electromagnetic response［J］.Chinese Journal of radio Science，2012，27（4）：766-772.（in Chinese）

［16］朱凯光，林 君，韩悦慧，等.基于神经网络的时间域直升机电磁数据电导率深度成像［J］.地球物理学报，2010，53（3）：743-750.ZHU Kaiguang，LIN Jun，HAN Yuehui，et al.Research on conductivity depth imaging of time domain helicopte r-borne electromagnetic data based on neural network［J］.Chinese J Geophys，2010，53（3）：743-750.（in Chinese）

［17］谢林涛，付志红，谢品芳，等.基于神经网络的视电阻率快速算法［J］.地球物理学进展，2009，24（4）：1527-1532.XIE Lintao，FU Zhihong，XIE Pinfang，et al.A fast algorithm of apparent resistivity based on neural network.Progress in Geoghys，2009，24（4）：1527-1532.（in Chinese）

［18］HUANG Haoping，RUDD J.Conductivity-depth imaging of helicopter-borne TEM data based on a pseudolayer half-space model［J］.Geophysics，2008，73：115-120.

［19］蒋邦远.实用近区磁源瞬变电磁法勘探［M］.北京：地质出版社，1998：162-168.