偏心孔缝箱体屏蔽效能电磁拓扑分析算法

张亚普 达新宇 谢铁城

（空军工程大学信息与导航学院，陕西 西安710077）

引 言

空间电磁环境日趋复杂，特别是电磁脉冲武器的研究与发展，对电子设备的生存构成极大威胁.箱体作为电子设备的重要组成部分，起着屏蔽大部分空间电磁能量的作用，然而由于通风、散热、显示等孔缝的存在，势必造成箱体屏蔽效能的下降，因此，开展箱体屏蔽效能研究，进而指导箱体设计，具有极强的研究意义和实用价值.

箱体屏蔽效能分析的实质是孔缝的电磁耦合效能分析，其研究理论主要分为两类：一类是数值方法，如矩量法［1］、时域有限差分法［2］、传输线矩阵法［3］等，该类方法虽然计算准确，但效率不高，在工程实践中难以推广应用；另一类是等效电路法，该类方法准确度较数值法差，但计算简便、迅速，应用性更强.等效电路法由Robinson［4］首先提出，该方法将孔等效为两端短路的共面传输线，箱体等效为终端短路的矩形波导.近年来，虽然不断有学者在Robinson研究（①只考虑了主模TE10；②孔或孔阵位于前面板中心；③入射波垂直极化）的基础上，从不同方面对等效电路法进行拓展和完善［5-11］，然而，改进模型均未能对箱体内部电磁场的过孔辐射效应进行合理建模，只考虑了外部电磁场的向内耦合.这类单向耦合模型，建立了计算箱体内部场的驻波态方程，而非行驻波态方程（实际情况），致使该类模型计算的内部耦合场值较实测值偏大.

电磁拓扑理论（Electromagnetic Topology Theory，EMT）是由美国学者Baum.C.E.于1974年在研究核电磁脉冲与复杂电子系统相互作用时首次提出的，随后Baum.C.E.又同Liu.T.K.和Tesche.F.M.一起推导了著名的BLT（Baum-Liu-Tesche）方程，用于计算经导线路径传播的电磁干扰能量［12］.2004年Tesche［13-14］等人提出了广 义BLT方程，用于研究电磁场的传播和耦合效应.2005年，Baum［15］采用广义BLT方程对孔、缝耦合问题进行了研究.节点散射矩阵是建立BLT方程的关键，Robinson等效电路法为孔缝节点散射矩阵的求解提供了新的思路，进而建立起简洁、准确的箱体孔缝耦合模型.

本文首先基于Robinson等效电路法，建立孔缝的等效电路模型，并采用微波电路理论计算孔缝二端口网络的散射矩阵；接着，基于电磁拓扑理论，建立偏心孔缝箱体耦合问题的广义BLT方程，并对其应用范围进行拓展；然后，对单孔、孔阵箱体的屏蔽效能进行仿真验证，并与CST数据进行对比；最后，采用该算法对单孔箱体屏蔽效能进行分析研究，得出防护结论.

1 理论分析

1.1 孔缝阻抗模型

如图1所示，在箱体（a×b×d）的x-y面上开有一矩形孔（wap×lap），入射横电磁波（Transverse Electromagnetic，TEM）电场幅值为V0，沿y轴极化，沿z轴传播，观测点J1、J3与开孔面距离分别为l、p.

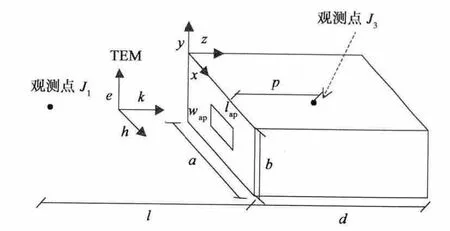
图1 平面波照射开孔箱体

依据Robinson理论，将矩形孔等效为终端负载Zl的共面传输线，其特性阻抗为

式中，we为孔缝有效高度，

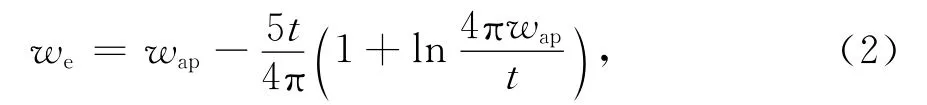
t为箱体厚度.

通过将共面传输线终端阻抗Zl转移到孔中心，可得孔缝等效阻抗Zap，引入偏心系数Cm，则任意位置孔缝的等效阻抗为［4］

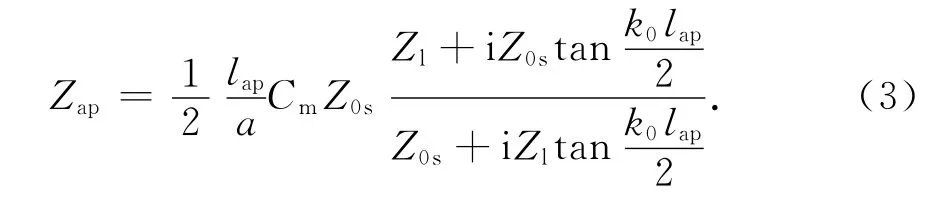
对于理想导体，Zl＝0；而实际情况，Zl由箱体材料特性决定

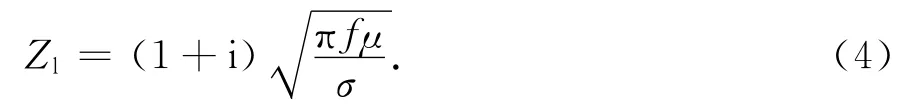
式中，μ、σ为材料的磁导率、电导率.

偏心系数Cm为［11］

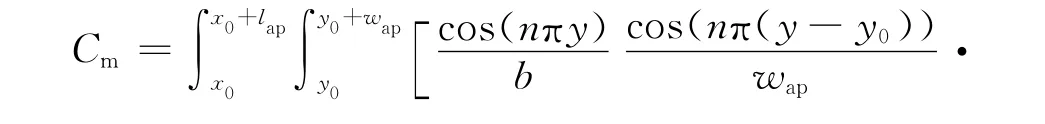
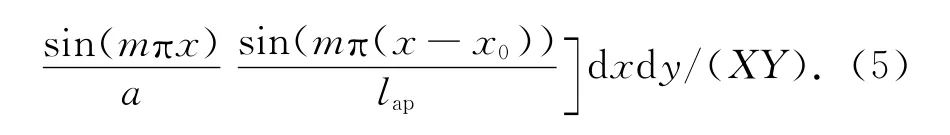
式中：m、n为沿x轴和z轴的模式数；X、Y为孔缝中心坐标；其他参数如图2所示.

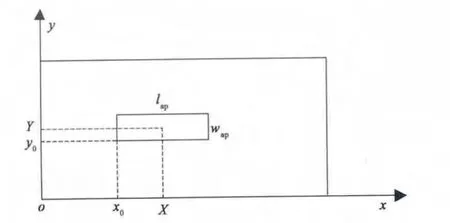
图2 孔缝平面

1.2 二端口网络模型

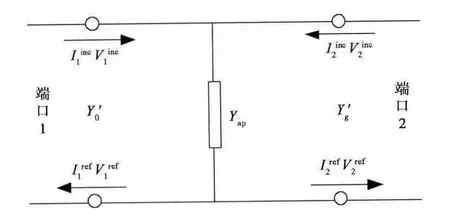
图3 孔缝二端口网络电路模型

图3所示电路模型的电路方程为

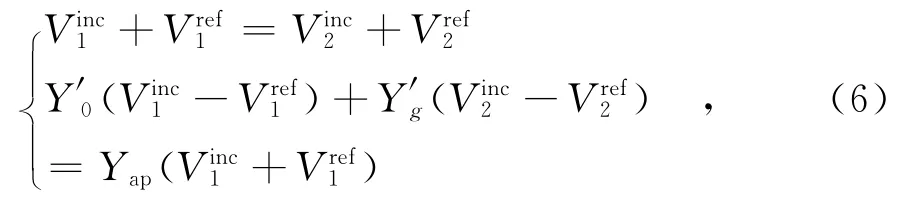
则

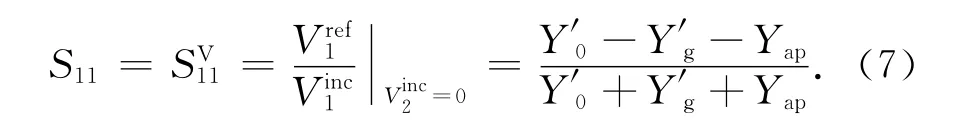
同理，可得S12、S21、S22，则孔缝二端口网络散射矩阵为

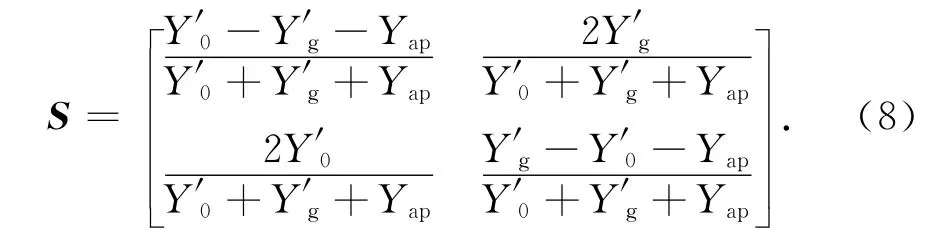
二端口网络散射矩阵S的准确性由孔缝等效阻抗Yap适用范围决定，即λ≫wap，通常

1.3 广义BLT方程

孔缝箱体耦合问题的等效电路模型如图4所示.平面波等效为内阻为Z′0，幅值为V0的电压源；自由空间和孔后箱体分别等效为特性阻抗Z′0和Z′g的传输线，且右侧传输线终端短路；孔缝等效为连接两传输线的二端口网络.

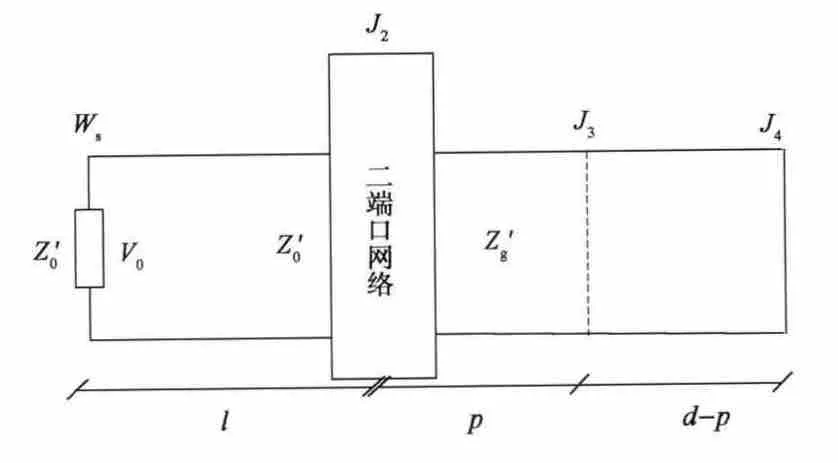
图4 孔缝耦合的等效电路模型

依EMT理论，孔缝箱体耦合问题信号流图如图5所示.其中，管道1表示自由空间，管道2和3表示矩形腔体，J1、J3分别为箱体外观测节点和箱体内观测节点，J2为孔节点，J4为矩形腔体末节点，WS为平面波激励为管道i上j节点的入射或反射电压波.

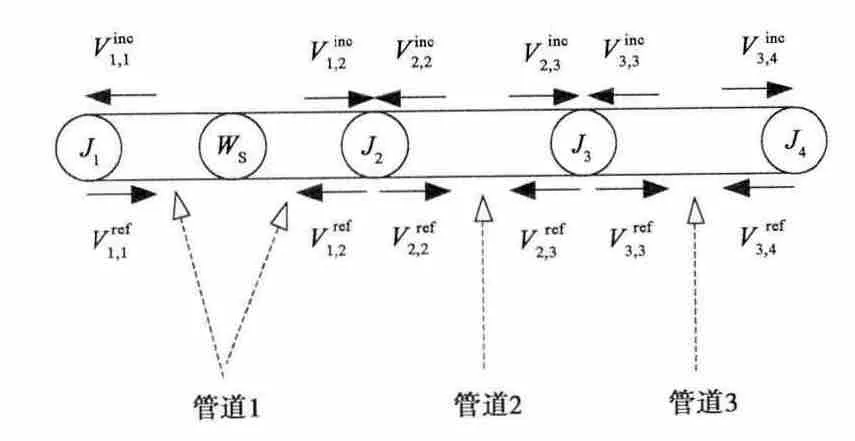
图5 孔缝耦合信号流图

传输方程为

散射方程为

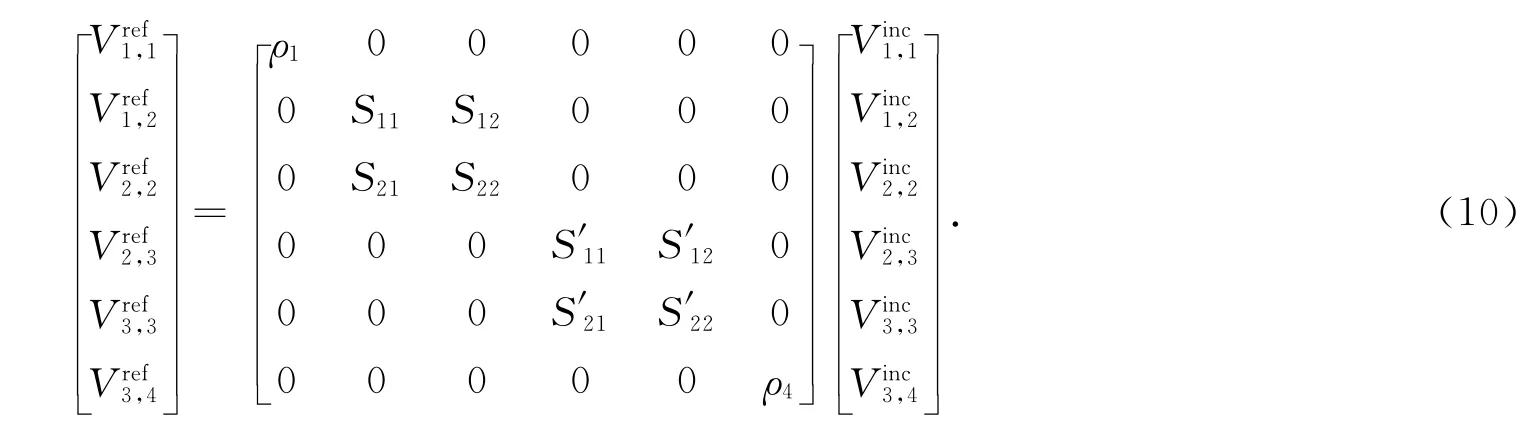
合并式（9）和（10）得BLT方程为

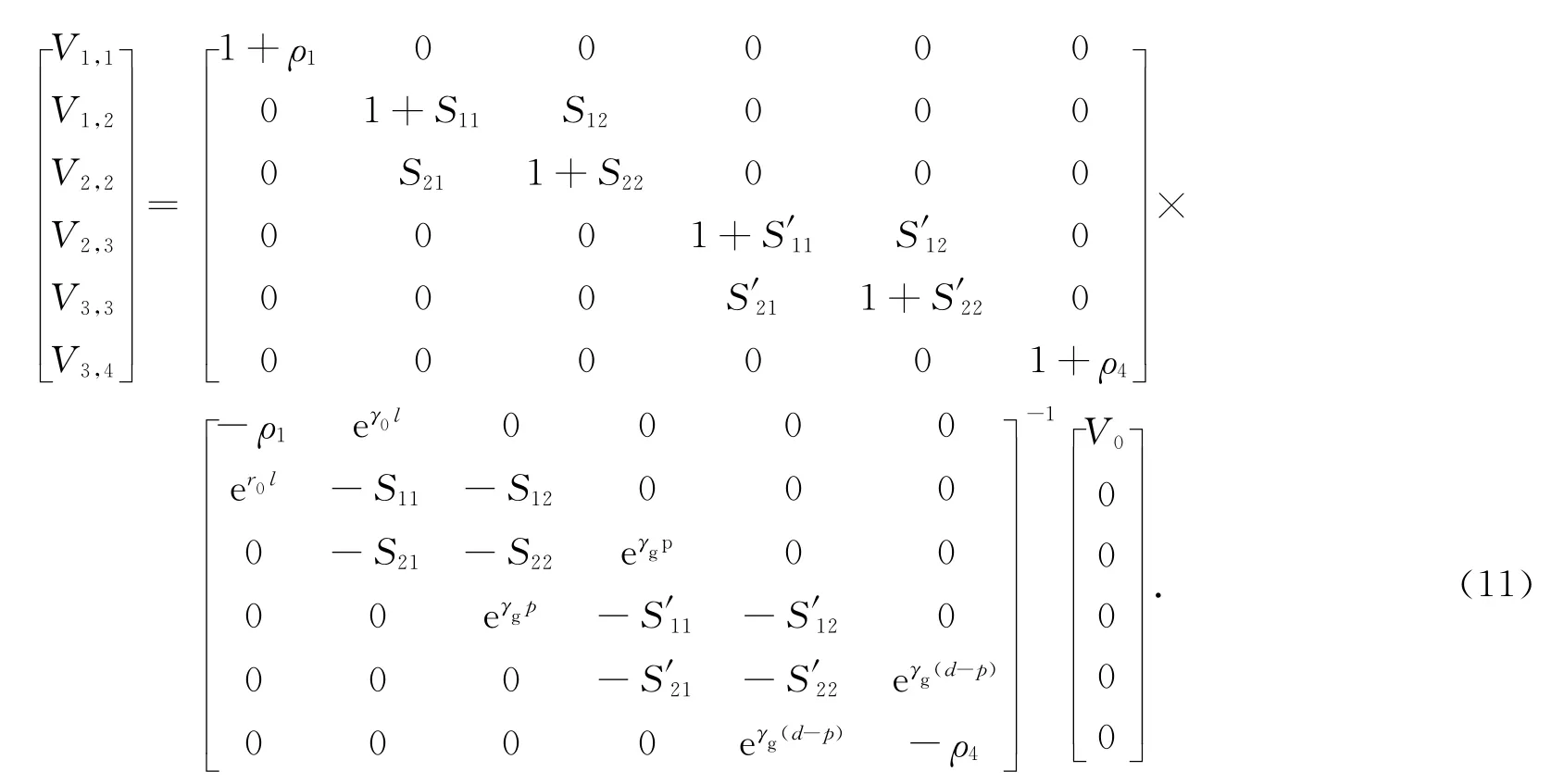
矩形波导中TE波的y轴电场分量为

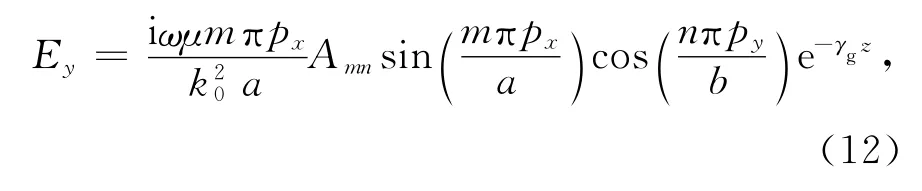
则由BLT方程计算的任意观测点TE波y轴电压分量为［10］

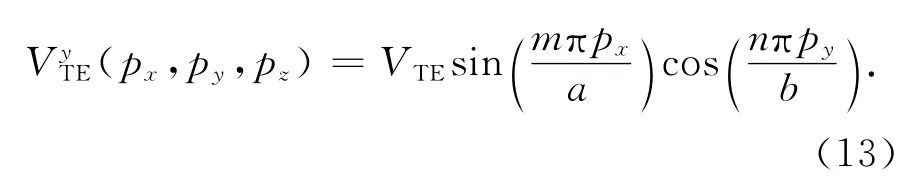
式中：（px，py，pz）为观测点坐标；VTE是由式（11）计算的观测点电压.

当横磁波（Transverse Magnetic，TM）传输时，γg、Zg由计算公式为

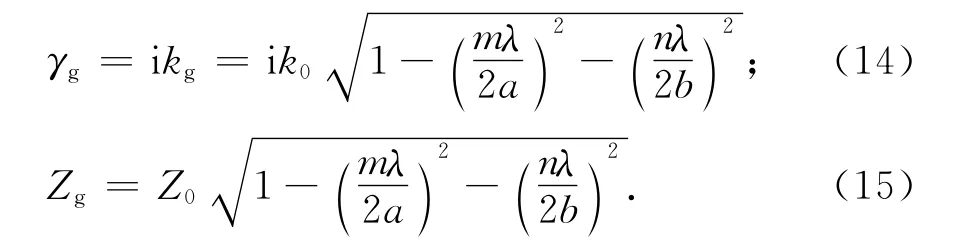
将式（14）、（15）带入式（11），可得TM波传输时，任意观测点的y轴电压分量，则任意观测点y轴电压分量为

从而得观测点总电压为

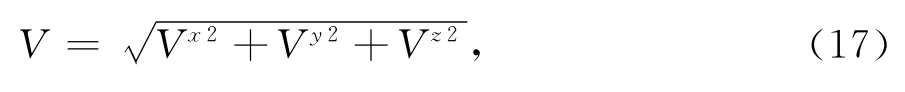
电磁屏蔽系数为

1.4 孔阵阻抗模型

当箱体存在图6所示孔阵时，孔间互耦现象必须考虑，因此，对式（3）进行修正，可得Yap为［4］

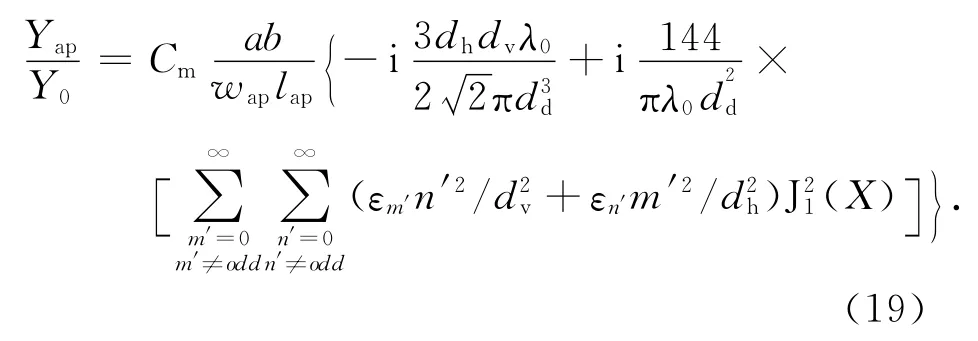
式中：λ0为自由空间波长；dv、dh如图6所示，当dv、dh和dd远小于波长时，式（19）中的二阶贝塞尔函数可忽略不计；m′，n′为横向、纵向的孔个数；J1为一类贝塞尔函数；

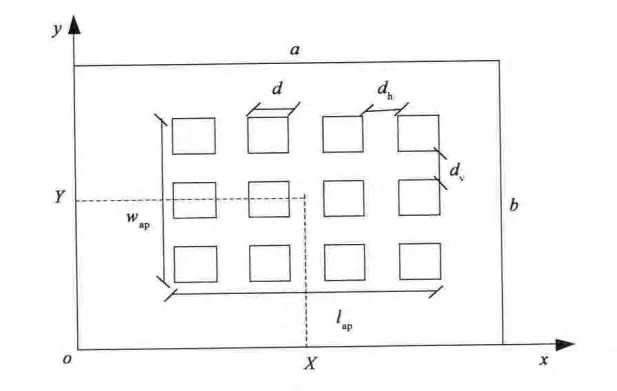
图6 箱体壁孔阵示意

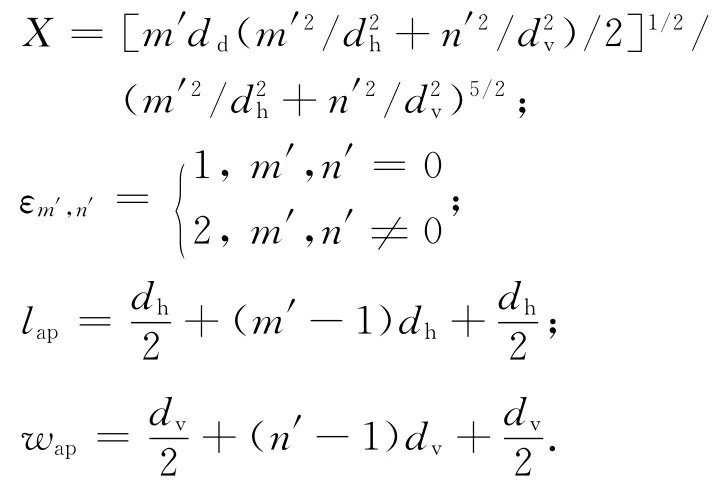
1.5 任意入射波拓展

对于任意入射波，孔缝箱体的屏蔽效能分析，可通过坐标分解的方法实现.如图7所示，入射波极化角为φ、仰角为θ、方位角为ψ，幅值为V0.

由于开孔平面为x-y面，故只需计算沿z轴传输的场参数Ex、Ey、kz，且有：

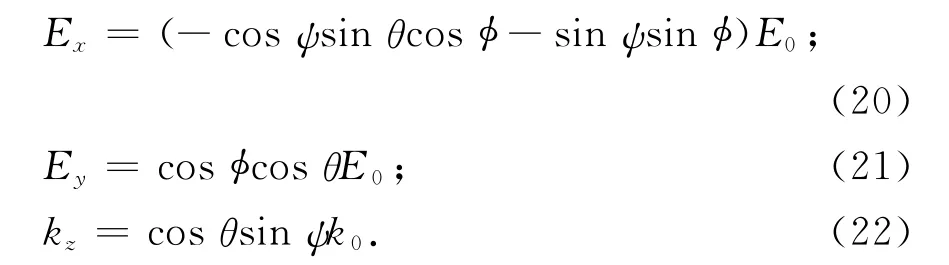
式（20）、（22）和式（21）、（22）分别带入式（11），求得Ex、Ey单独激励下，观测点J3的电压值VJ3，x、VJ3，y，则其y轴电压分量进而由式（17）得总电压值，再由式（18）计算屏蔽系数.

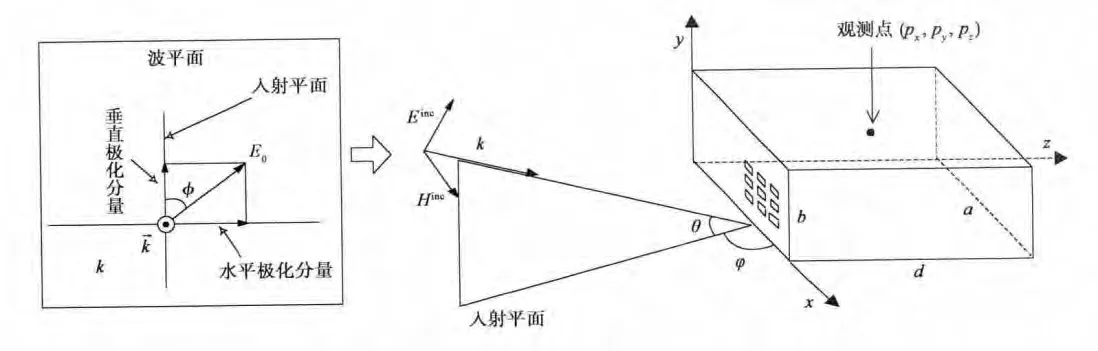
图7 任意入射波照射箱体

2 实验结果分析

基于CST仿真数据，对上述广义BLT方程计算结果的准确性进行验证.仿真实验环境为：Interl（R）Core（TM）i3-2120＠3.3GHz 3.29GHz CPU，2G内存，Windows XP系统，Matlab7.8，CST 2011.

仿真实验基本参数如下：

2）箱体参数：a＝300mm，d＝300mm，b＝120 mm，t＝1.5mm.

3）单孔参数：lap＝100mm，wap＝50mm.

4）孔阵参数：dv＝22mm，dh＝22mm，dd＝20 mm，m′＝3，n′＝3.

5）J3散射矩阵

6）l为任意常数.

在上述基本参数前提下，以X、Y、px、py、pz为可变参数，分别对单孔和孔阵箱体的屏蔽效能进行仿真分析（X、Y为孔心坐标；px、py、pz为观测点坐标）.

2.1 单孔箱体仿真验证

针对单孔箱体模型设计了4组验证性实验，实验参数如表1所示.

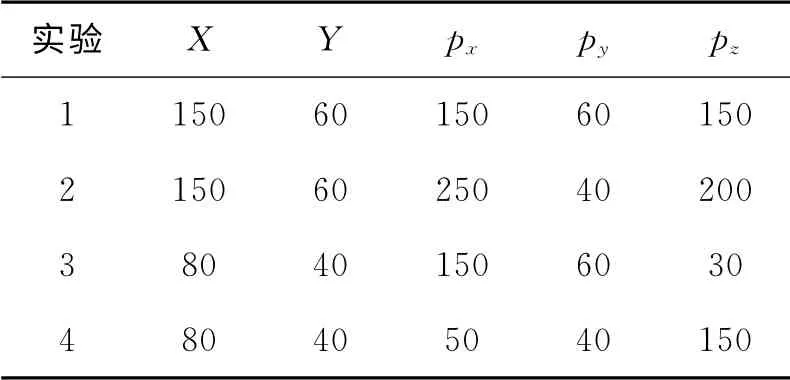
表1 单孔实验参数 单位：mm

图8所示为BLT算法与F.Tahar Belkacem算法对单孔箱体屏蔽效能的仿真实验.两算法仿真结果与CST数据对比，易知：0～2GHz频域内BLT算法明显优于F.Tahar Belkacem算法；但当频率高于1.5GHz时，随着频率的升高BLT计算结果误差增大；当频率达到1.5GHz时，λ＝4wap，达到单孔二端口网络散射矩阵S精度满足的临界波长.因此，当频率高于1.5GHz时，BLT计算出现较大误差.

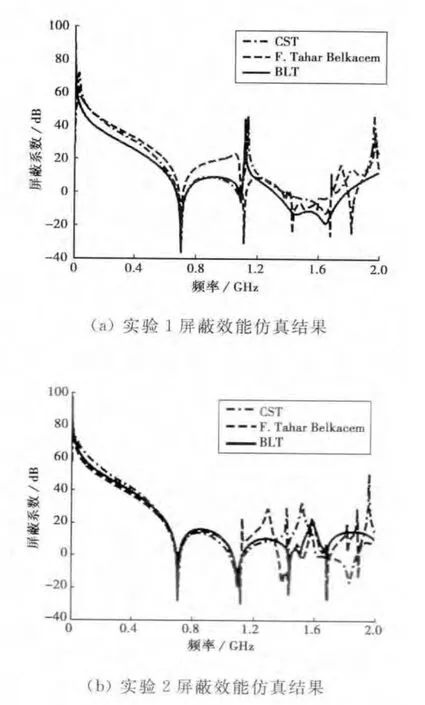
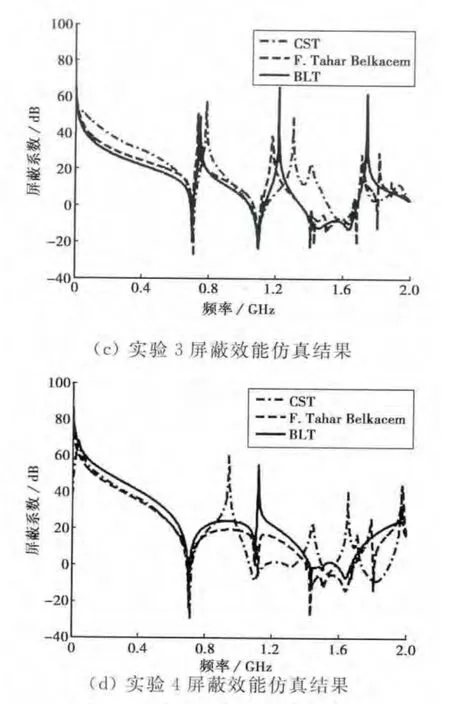
图8 单孔箱体屏蔽效能验证仿真

图8（a）、（b）为中心单孔箱体不同测试点处的屏蔽效能分析结果.两图中BLT较准确地计算出箱体700、1 100和1 600MHz三个谐振点，图8（a）对1.5～2GHz频域范围内的屏蔽效能计算结果优于图8（b），证明了BLT方法对单孔箱体中轴线上观测点的屏蔽系数计算更为精确.图8（c）、（d）为偏心单孔箱体不同测试点处的屏蔽效能分析结果.两图中BLT较准确地计算出箱体700、1 100MHz两个谐振点.

2.2 孔阵箱体仿真验证

针对孔阵箱体模型设计了4组验证性实验，实验参数如表2所示.

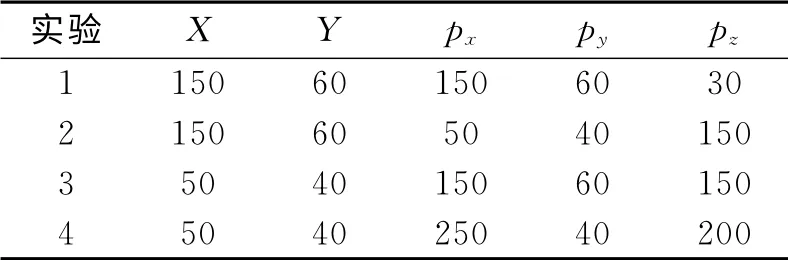
表2 孔阵实验参数 单位：mm

图9所示为BLT算法与F.Tahar Belkacem算法对孔阵箱体屏蔽效能的对比仿真，不难发现，BLT计算的屏蔽曲线与CST仿真结果在0～2GHz频域范围内吻合度较高，且明显优于F.Tahar Belkacem算法.

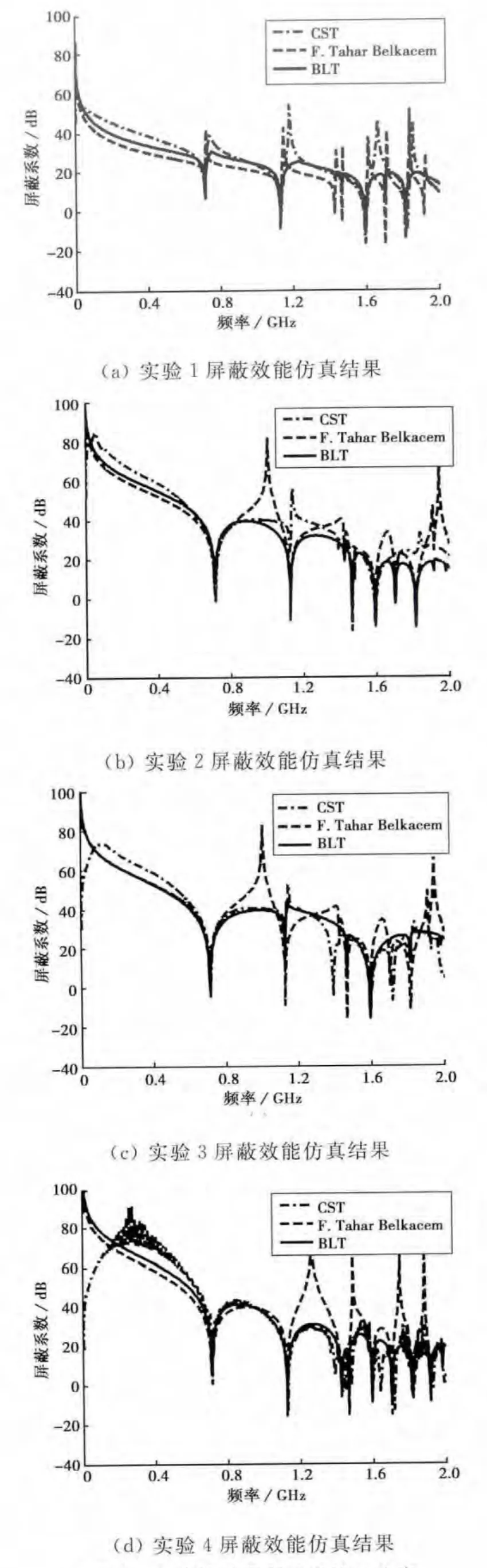
图9 孔阵箱体屏蔽效能验证仿真

图9（a）、（b）为中心孔阵箱体不同测试点处的屏蔽效能分析结果.图9（a）中BLT较准确地计算出箱体700、1 100、1 600、1 820MHz四个谐振点，优于图9（b）的三个谐振点，可见，BLT方法对孔阵箱体中轴线上观测点的屏蔽系数计算更为精确.图9（c）、（d）为偏心单孔箱体不同测试点处的屏蔽效能分析结果.两图中BLT较准确地计算出箱体700、1 120、1 600、1 710、1 820、1 930MHz六个谐振点.

与单孔箱体分析时不同，图9中BLT对1.5～2GHz频域范围内的屏蔽系数也能较为准确地给出计算结果，证明了该孔阵阻抗模型比单孔阻抗模型更为准确，且适用范围更广（0～2GHz）.

2.3 单孔箱体屏蔽效能分析

基于电磁拓扑模型，对中心单孔箱体的屏蔽效能进行分析研究，实验参数如表3所示.

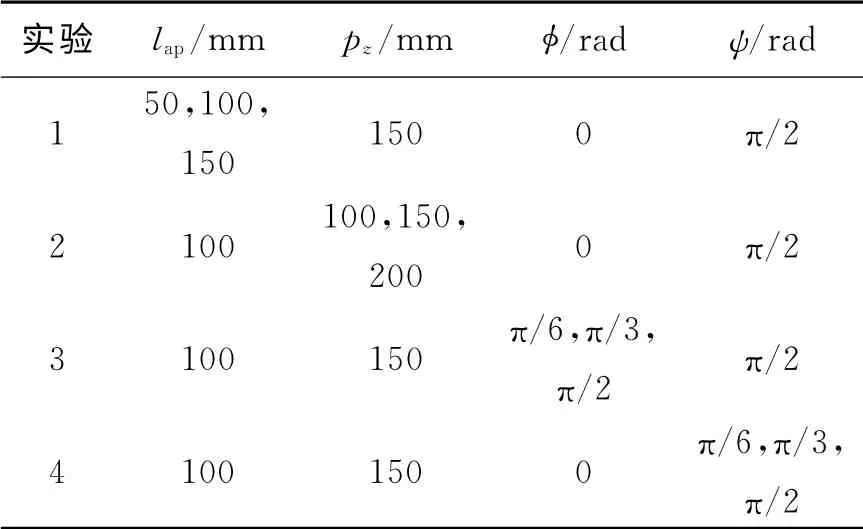
表3 实验参数

图10（a）所示为孔宽变化时，单孔箱体屏蔽效能曲线，不难发现，单孔箱体屏蔽效能随孔宽增加而下降.因为，在孔高不变前提下，随着孔宽的增加，开孔面积不断增加，透过孔缝进入箱体内部的电磁能量相应随之增加，这势必导致箱体内部耦合场增强，进而导致箱体屏蔽效能降低.

图10（b）所示为观测距离变化时，单孔箱体屏蔽效能曲线.易知，屏蔽系数在0～700Hz频域内，随距离增加而增加；频率高于700MHz时，屏蔽系数随距离的变化规律不明显，这主要是由不同频率的波在箱体内的驻波点位置不同所导致的，因此，屏蔽效能曲线在0～2GHz频域内与观测距离无明显线性关系.

图10（c）所示为极化角变化时，单孔箱体屏蔽效能曲线.由图可知，屏蔽效能随极化角的增大而增强，可见，当电场极化方向垂直孔缝长边时，耦合场值最大.

图10（d）所示为方位角变化时，单孔箱体屏蔽效能曲线.由图可知，屏蔽效能随方位角的增大而下降，可见，入射场垂直孔缝平面时，耦合场值最大.

3 结 论

基于Robinson等效电路理论和偏心理论，提出了偏心孔逢箱体屏蔽效能分析的EMT模型.该模型建立了箱体参数、孔逢参数与屏蔽系数间的直接映射，在保证计算效率的前提下，仍具有较高计算精度，可用于屏蔽箱体的快速电磁兼容设计与整改，实用性较强.对单孔和孔阵箱体的验证性仿真，证明了该方法的有效性，并得出单孔箱体屏蔽效能特性：

1）孔缝面积增大，箱体屏蔽效能下降.

2）入射场极化方向垂直于孔缝长边，屏蔽效能最差.

3）入射场传输方向垂直于孔缝平面，屏蔽效能最差.

［1］WANG T，HARRINGTON R F，MAUTZ J R.Electromagnetic scattering from and transmission through arbitrary apertures in conducting bodies［J］.IEEE Trans Antennas Propag，1990，38（11）：1805-1814.

［2］JIAO C，LI L，CUI X，et al.Subcell FDTD analysis of shielding effectiveness of a thin-walled enclosure with an aperture［J］.IEEE Trans Magn，2006，42（4）：1075-1078.

［3］RENDER M C，MARVIN A C.A multiple mode equivalent transmission line method of crosstalk between conductors in shielded environments［J］.IEEE Trans Electromagn Compat，1995，37（3）：488-494.

［4］ROBINSON M P，BENSON T M，CHRISTOPOULOS C，et al.Analytical formulation for the shielding effectiveness of enclosures with apertures［J］.IEEE Trans Electromagn Compat，1998，40（3）：240-248.

［5］石 丹，沈远茂，高攸纲.有孔屏蔽腔的高次模分析［J］.电波科学学报，2009，24（3）：510-513.SHI Dan，SHEN Yuanmao，GAO Yougang.High order modes analysis on shielding effectiveness of enclosure with off-center aperture［J］.Chinese Journal of Radio Science，2009，24（3）：510-513.（in Chinese）

［6］石 丹.平面波斜入射到有孔腔体的屏蔽效能分析［J］.电波科学学报，2011，26（4）：678-682.SHI Dan.Shielding effectiveness analysis of enclosure with center aperture irradiated by oblique incident plane wave［J］.Chinese Journal of Radio Science，2011，26（4）：678-682.（in Chinese）

［7］张旭锋，李 颖，倪谷炎，等.有孔腔体屏蔽效应分析的混合模型［J］.电波科学学报，2011，26（1）：25-29.ZHANG Xufeng，LI Ying，NI Guyan，et al.Hybrid model to evaluating shielding effectiveness of cavity with apertures［J］.Chinese Journal of Radio Science，2011，26（1）：25-29.（in Chinese）

［8］KONEFAL T，DAWSON J F，MARVIN A C，et al.A fast multiple mode intermediate level circuit model for the prediction of shielding effectiveness of a rectangular box containing a rectangular aperture［J］.IEEE Trans Electromagn Compat，2005，47（4）：678-691.

［9］DEHKHODA P，TAVAKOLI A，MOINI R.An efficient and reliable shielding effectiveness evaluation of a rectangular enclosure with numerous apertures［J］.IEEE Trans Electromagn Compat，2008，50（1）：208-212.

［10］SHIM J J，KAM D G，KWON J H，et al.Circuital modeling and measurement of shielding effectiveness against oblique incident plane wave on apertures in multiple sides of rectangular enclosure［J］.IEEE Trans Electromagn Compat，2010，52（3）：566-577.

［11］BELKACEM F T，BENSETTI M，BOUTAR A G，et al.Combined model for shielding effectiveness estimation of a metallic enclosure with apertures［J］.IET Sci Meas Technol，2011，5（3）：88-95.

［12］BAUM C E，LIU T K，TESCHE F M.On the Analysis of General Multi-conductor Transmission-line Networks［R］.Interaction Notes 350，1978：1-38.

［13］TESCHE F M，BUTLER C M.On the Addition of EM field Propagation and Coupling Effects in the BLT Equation［R］.Interaction Notes 588，2003：1-43.

［14］TESCHE F M，KEEN J，BUTLER C M.Example of the Use of the BLT Equation for EM Field Propagation and Coupling Calculations［R］.Interaction Notes 591，2004，1-34.

［15］BAUM C E.Including Apertures and cavities in the BLT formalism［J］.Electromagnetics，2005，25（7／8）：623-635.