交替隐式时域方法精确实现理想导体边界

刘丽娜 朱 峰 徐常伟 牛大鹏 邱日强

（西南交通大学电气工程学院，四川 成都610031）

引 言

时域有限差分（Finite-Difference Time-Domain，FDTD）方法在很多领域得到了广泛应用［1-3］，但是Courant稳定条件限制了时间步长，数值色散条件对空间步长提出了要求，导致FDTD方法针对较复杂模型的电磁场数值计算时间过长.Namiki提出的交替方向隐式时域有限差分（Alternating Direction Implicit Finite-Difference Time-Domain，ADI-FDTD）方法［4］很好地消除了Courant稳定条件对时间步长的影响.ADI-FDTD方法将FDTD方法中n→n＋1的过程分成的两个子时间过程，将Maxwell方程离散成隐式差分方程，通过解待求场分量系数矩阵，得到场分量，完成时间的迭代递推.针对ADI-FDTD方法，国内外学者展开了一系列关于算法稳定性［5］.数值色散［6］、计算精度［7］和适用于ADI-FDTD方法的吸收边界条件［8］等内容的研究.此外，改进ADI-FDTD方法、分析等离子体［9］和有耗介质［10］的电磁传播特性以及ADI-FDTD方法减缩时域有限差分（Reduced Finite-Difference Time-Domain，R-FDTD）方法［11］等方法相结合的探讨都是研究的热点.最近提出的理想电磁导体（Perfect Electromagnetic Conductor，PEMC）边界［12］包括了理想电导体（Perfect Electric Conductor，PEC）边界和理想磁导体（Perfect Magnetic Conductor，PMC）边界，人工磁导体［13］在天线领域的应用也备受关注.PEC边界上的切向电场和PMC边界上的切向磁场均为零［14］.当ADI-FDTD计算区域中出现PEC或PMC边界时，由于部分场分量被置零，导致待求场分量系数发生变化，如果不对系数进行修正，场分量的计算结果会出现误差.

本研究考虑三维ADI-FDTD情况，在得到待求场分量系数之前应用理想导体边界条件，推导出ADI-FDTD方法在理想导体边界处待求场分量的修正系数.对于PEC边界和PMC边界条件，作为理想导体表面还是作为对称面截断计算空间的不同情况加以区分，讨论了修正系数与传统ADI-FDTD系数的区别.采用修正系数计算了单个金属立方体和具有对称结构的两个金属立方体的双站雷达散射截面（Radar Cross-Section，RCS），计算结果与传统ADI-FDTD方法和FDTD方法的计算结果进行比较，结果表明：对于理想导体表面，采用修正系数的计算结果与传统FDTD方法计算结果更为吻合；理想导体边界条件作为对称面截断计算空间的情况，采用修正系数的计算结果与传统ADI-FDTD方法计算结果相同，验证了理论推导.修正系数方法处理实现理想导体边界的优点在于具有统一的表达式，无需区分理想导体边界是理想导体表面还是截断计算空间的对称面，计算理想导体表面较传统ADIFDTD方法有较小的计算误差.

1 理论分析

1.1 PEC边界的ADI-FDTD实现

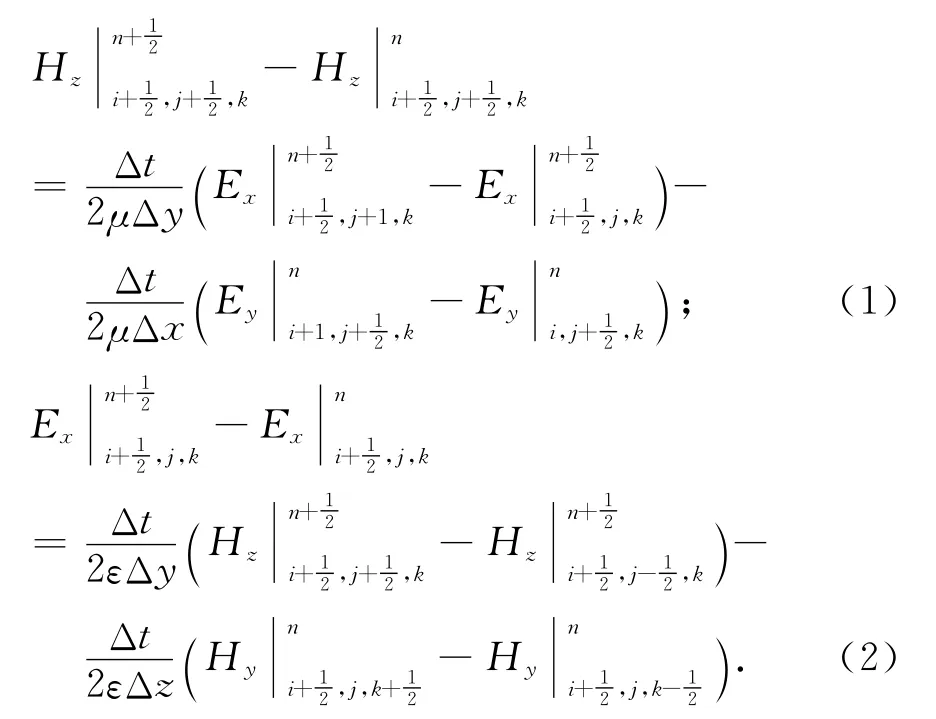
将式（2）代入式（1）整理可以得到传统ADI-FDTD方法计算Hz的公式：

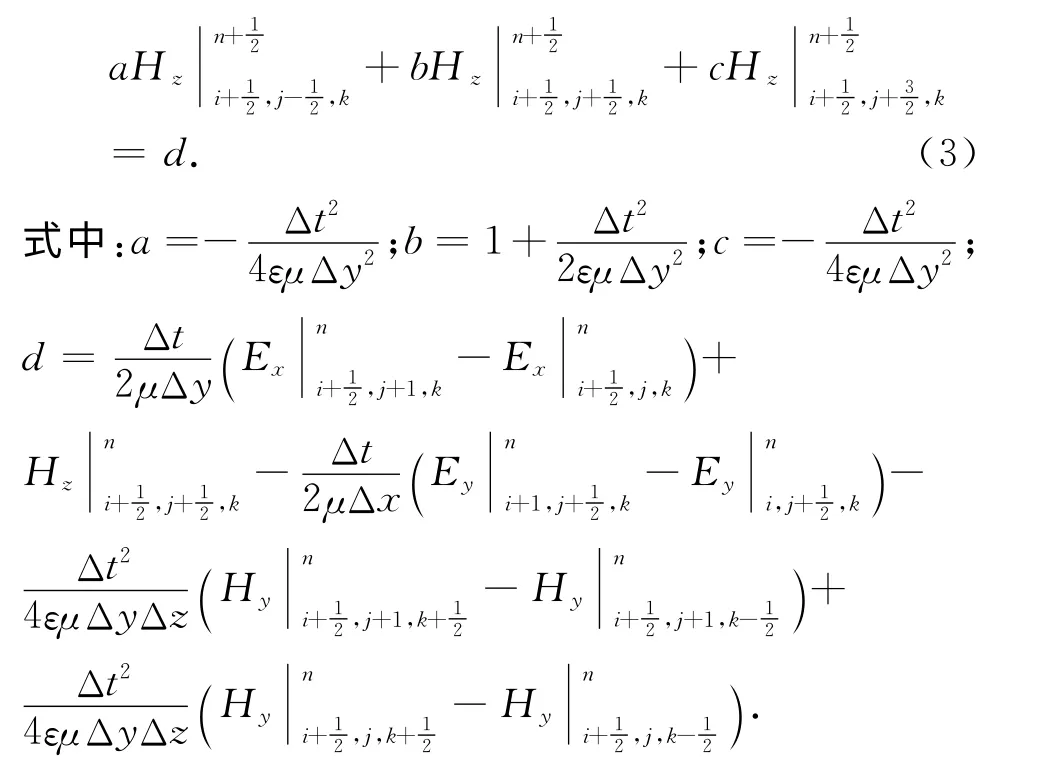
①传统ADI-FDTD方法：得到式（3）之后将PEC边界条件代入得到

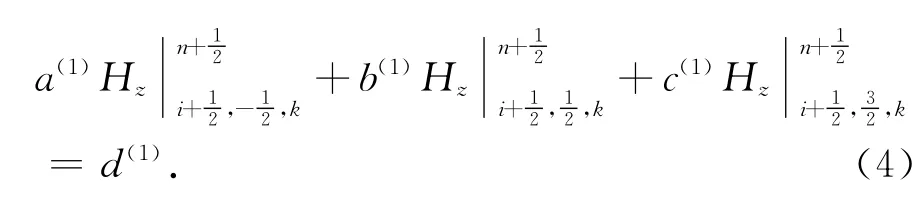
式中：系数a（1）＝a；b（1）＝b；c（1）＝c；d（1）＝

②修正系数方法：得到式（3）之前，即在式（2）代入式（1）之前考虑PEC边界条件仅将用式（2）展开代入式（1）得到

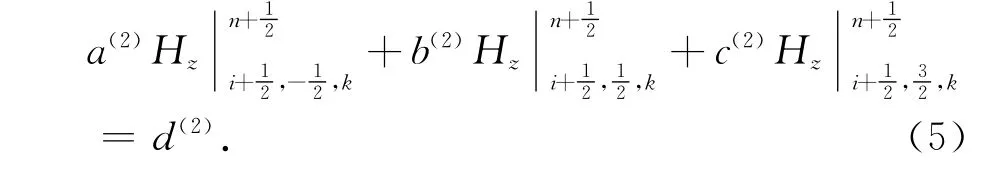
此处需要对PEC边界的情况加以区别对待：当PEC边界作为理想电导体表面时，在理想电导体内部有，此处为了和修正系数方法对比，修正传统ADI-FDTD方法的式（4）系数a（1）＝0，其他系数b（1），c（1），d（1）不变.传统ADI-FDTD方法与修正系数方法比较的结果是的系数不同；当PEC边界作为对称面截断计算空间时，由镜像原理可以得到将传统ADI-FDTD方法的式（4）中两个场分量合并，可以得到和修正系数方法完全相同的场分量表达式.

1.2 PMC边界的ADI-FDTD实现

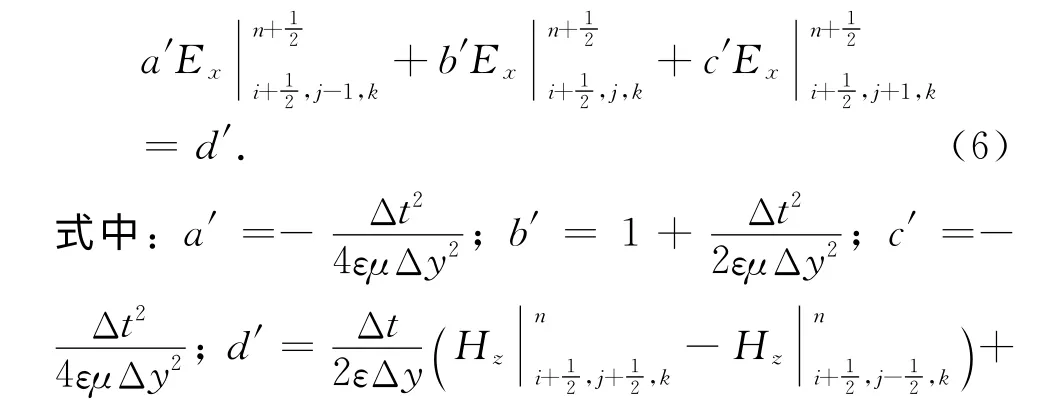
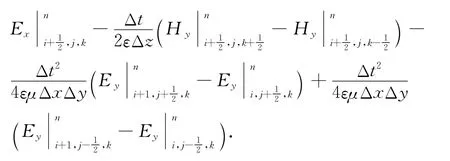
①传统ADI-FDTD方法：得到式（6）之后将PMC边界条件代入得到

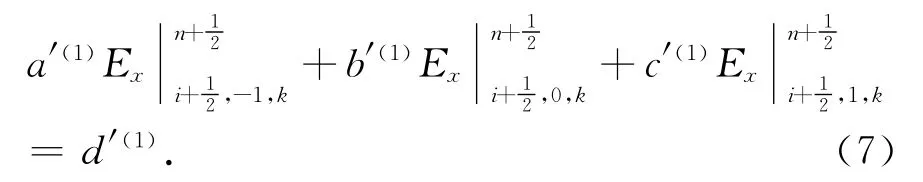
式中：系数a′（1）＝a′；b′（1）＝b′；c′（1）＝c′；d′（1）＝

②修正系数方法：得到式（6）之前，即在式（1）代入式（2）之前考虑PMC边界条件0，仅将用式（1）展开代入式（2）得到

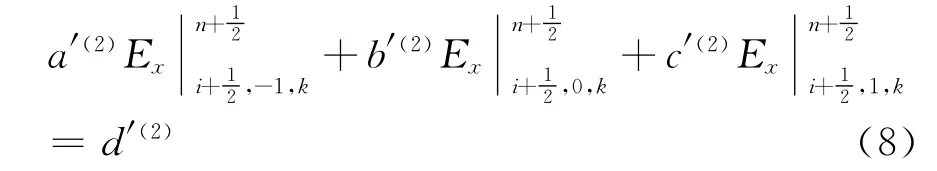
此处需要对PMC边界的情况加以区别对待：当PMC边界作为理想磁导体表面时，在理想磁导体内部有此处为了和修正系数方法对比，修正传统ADI-FDTD方法的式（7）系数a′（1）＝0，其他系数b′（1），c′（1），d′（1）不变.传统ADI-FDTD方法与修正系数方法比较的结果是的系数不同；当PMC边界作为对称面截断计算空间时，由镜像原理得到，将传统ADI-FDTD方法的式（7）中两个场分量合并，得到和修正系数方法完全相同的场分量表达式.

2 数值计算结果

采用修正系数方法计算单个金属立方体和对称的两个金属立方体的双站RCS，与传统ADI-FDTD方法和FDTD方法的计算结果进行比较.平面波频率3GHz沿z方向入射，x方向极化.计算空间由PML吸收边界截断.FDTD算法的时间步长Δt＝8.333×10-12s，空间步长Δx＝Δy＝Δz＝0.005m，修正系数方法和传统ADI-FDTD方法的时间步长ΔtADI＝5Δt.

算例1 理想导体表面的情况：计算一个金属立方体的双站RCS，金属立方体每个面都采用PEC边界条件，金属立方体边长为L＝0.1m.计算模型如图1所示，三种方法对比计算得到的金属立方体的双站RCS如图2所示.

分析对比计算结果，对于设置在导体表面的PEC边界，三种方法的计算结果吻合，修正系数方法的计算结果更接近FDTD方法的计算结果.说明了导体表面采用修正系数计算的正确性和必要性.

图1 算例1的计算模型

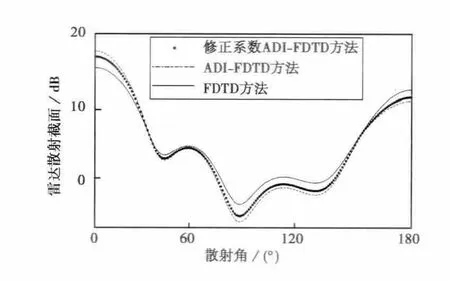
图2 不同方法计算算例1的双站RCS

算例2 PMC边界截断对称空间的情况：计算对称的两个金属立方体的双站RCS，每个金属立方体边长为L＝0.1m，两个金属立方体中心间距0.2 m.在与y轴垂直的整个计算区域的对称面处设置PMC边界截断，只计算FDTD方法的一半空间.计算模型如图3所示，三种方法对比计算得到的两个金属立方体的双站RCS如图4所示.

分析对比计算结果，对于PMC边界作为对称面截断计算空间的情况，修正系数方法和传统ADIFDTD方法的结算结果吻合.截断面的表面虽然同样满足PMC边界条件，但是由于截断面以外的场分量不再为零，所以，采用镜像原理从理论上得到的修正系数方法和传统ADI-FDTD方法等同的结论得以验证.

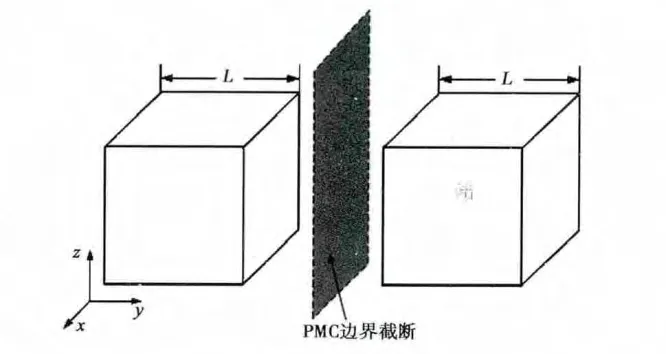
图3 算例2的计算模型

图4 不同方法计算算例2的双站RCS

3 结 论

本研究针对三维ADI-FDTD方法，在得到待求场分量系数之前应用理想导体边界条件，推导出在理想导体边界处与传统ADI-FDTD方法不同的待求场分量的修正系数.当理想导体边界作为理想电（磁）导体表面时，修正系数与传统ADI-FDTD方法的系数不同；当理想导体边界作为对称空间的截断面，应用镜像原理，修正系数与传统ADI-FDTD方法的系数相同.计算了单个金属立方体和对称的两个金属立方体的双站RCS，采用修正系数的计算结果与传统ADI-FDTD方法和FDTD方法的计算结果进行了对比.对于理想导体表面，采用修正系数的计算结果与传统FDTD方法计算结果更为吻合，因此，建议在处理导体表面时，在得到待求场分量系数之前就考虑理想导体边界条件，采用修正系数计算场分量，以便得到更精确的场分量的值.理想导体边界条件作为对称面截断计算空间时，采用修正系数的计算结果与传统ADI-FDTD方法计算结果相同，与理论推导结果一致.针对将理想导体边界条件作为理想导体表面和截断计算空间的对称面的两种情况，修正系数方法实现理想导体边界的优点在于具有统一的表达式.本研究探讨的内容，有助于减小ADI-FDTD方法实现PEC边界和PMC边界的计算误差.

［1］任晶晶，柴守刚，陈卫东.基于混合计算方法的脉冲超宽带穿墙散射建模［J］.电波科学学报，2012，27（5）：859-866.REN Jingjing，CHAI Shougang，CHEN Wei-dong.Hybrid technique combining time domain ray-tracing and FDTD method for IR-UWB signal through-thewall scattering modeling［J］.Chinese Journal of Radio Science，2012，27（5）：859-866.（in Chinese）

［2］姜彦南，李思敏，曹卫平，等.相控阵天线时域有限差分计算中激励源分析［J］.电波科学学报，2011，26（5）：894-898.JIANG Yannan，LI Simin，CAO Weiping，et al.Excitation source in FDTD method calculate phased array antenna［J］.Chinese Journal of Radio Science，2011，26（5）：894-898.（in Chinese）

［3］张 品，陈亦望，傅 强.一种提高内存使用效率的时域有限差分算法［J］.电波科学学报，2011，26（4）：814-819.ZHANG Pin，CHEN Yiwang，FU Qiang.A memoryefficient FDTD algorithm［J］.Chinese Journal of Radio Science，2011，26（4）：814-819.（in Chinese）

［4］NAMIKI T.3-D ADI-FDTD method-unconditionally stable time-domain algorithm for solving full vecto Maxwell＇s equations［J］.IEEE Trans Microwave Theory and Techniques，2000，48（10）：1743-1748.

［5］GUILIN S，TRUEMAN C W.Some fundamental characteristics of the one-dimensional alternate-directionimplicit finite-difference time-domain method［J］.IEEE Trans Microwave Theory and Techniques，2004，52（1）：46-52.

［6］ANPING Z.The influence of the time step on the numerical dispersion error of an unconditionally stable 3-D ADI-FDTD method：a simple and unified approach to determine the maximum allowable time step required by a desired numerical dispersion accuracy［J］.Microwave and Optical Technology Letters，2002，35（1）：60-65.

［7］GONZALEZ G S，LEE T，HAGNESS S C.On the accuracy of the ADI-FDTD method［J］.IEEE Antennas and Wireless Propagation Letters，2002，1：31-34.

［8］PEREDA J A，SERROUKH A，GRANDE A，et al.Implementation of absorbing boundary conditions based on the second-order one-way wave equation in the LOD-and the ADI-FDTD methods［J］.IEEE Antennas and Wireless Propagation Letters，2012，11：981-983.

［9］殷 雄，赵振维，张 厚，等.等离子体散射分析的改进型交替隐式时域方法［J］.电波科学学报，2013，28（2）：354-361.YIN Xiong，ZHAO Zhenwei，ZHANG Hou，et al.An improved ADI-FDTD method for computing the scattering properties of unmagnetized plasma［J］.Chinese Journal of Radio Science，2013，28（2）：354-361.（in Chinese）

［10］张玉廷，蔡 智，刘 胜.交替隐式时域有限差分分析有耗介质电磁波传播［J］.电波科学学报，2011，26（6）：1088-1094.ZHANG Yuting，CAI Zhi，LIU Sheng.Electromagnetic wave propagation in loss media based on ADIFDTD［J］.Chinese Journal of Radio Science，2011，26（6）：1088-1094.（in Chinese）

［11］JIN X H，CHEN Y W，ZHANG P.An algorithm of 3-D ADI-R-FDTD based on non-zero divergence relation-ship［J］.Advanced Materials Research，2011，317-319：1172-1176.

［12］VAHID N，MOHAMMAD S，MOJTABA D，et al.Reflection from stratified media backed by aperfect electromagnetic conductor（PEMC）［J］.IEEE Trans Antennas and Propagation，2012，60（10）：4969-4973.

［13］鲁 磊，屈绍波，马 华，等.宽带雷达散射截面减缩人工磁导体复合结构［J］.物理学报，2013，62（3）：170-175.LU Lei，QU Shaobo，MA Hua，et al.A broadband artificial magnetic conductor composite structure for radar cross section reduction［J］.Acta Physica Sinica，2013，62（3）：170-175.（in Chinese）

［14］张 岩，吕善伟，苗俊刚，等.FDTD-PWS法用于分析毫米波透镜天线焦面场［J］.北京航空航天大学学报，2007，33（6）：682-685.ZHANG Yan，LÜShanwei，MIAO Jungang，et al.Hybrid FDTDPWS method for focal field analysis of lens antenna at millimeter wave band［J］.Journal of Beijing University of Aeronautics and Astronautics，2007，33（6）：682-685.（in Chinese）