扩展孔径的电磁矢量多入多出雷达目标定位算法
樊劲宇 苏卫民 顾 红 王 钊
(南京理工大学电子工程与光电技术学院,江苏 南京210094)
引 言
源于无线通信多输入多输出(Multiple-Input Multiple-Output,MIMO)技术的双基地MIMO雷达最近受到了广泛关注.其最早是由Parker.P等人在文献[1]中提出的,相比传统雷达而言具有更大的阵列孔径、更高的阵列自由度和更好的低截获性能[2-4].双基地MIMO雷达目标定位主要是利用阵列信号处理算法同时测量目标的波达角(Direction of Departure,DOA)与波离角(Direction of Departure,DOD),从而实现交叉定位.文献[5]将多重信号分类(Multiple Signal Classification,MUSIC)算法应用到MIMO雷达,利用2维谱峰搜索同时估计目标的DOD和DOA.文献[6]利用两次独立的旋转不变子空间技术(Estimating Signal Parameters via Rotational Invariance Techniques,ESPRIT)算法分别估计多个目标的DOD和DOA,避免了谱峰搜索,但需要额外的配对算法.文献[7]利用MIMO雷达输出数据的多维结构构造测量张量,通过CP分解(CANDECOMP/PARAFAC decomposition)求解其因子矩阵,可以同时估计多个目标的方位向波离角(Azimuth DOD,ADOD)、俯仰向波离角(Elevation DOD,EDOD)、方位向波达角(Azimuth DOA,ADOA)、俯仰向波 达角(Elevation DOA,EDOA),各参数自动配对.以上算法均要求阵元间距小于半波长,否则得到的角度估计值存在周期性模糊.
电磁矢量天线(Electromagnetic Vetor Antenna,EMVA)同时获取信号的空域信息和极化域信息,具有比传统阵列更高的检测性能,不受阵元间距限制.文献[8]提出了一种矢量叉积测向法(Vector Cross-Product Direction-Finding,VCPDF),仅用一个完备的EMVA实现目标2维DOA估计.该阵元由3对正交放置的电磁偶极子对组成,对阵元位置无特殊要求,但估计精度不高.文献[9]利用EMVA阵列获取入射波电磁场矢量的方向信息,以解决ESPRIT算法中的角度模糊问题,但仅针对无源测向.文献[10]将完备的EMVA用于MIMO通信领域,利用偶极子天线的极化分集特性增大了信道容量.文献[11]将EMVA技术引入MIMO雷达,实现了目标DOD和DOA联合估计,通过扩展孔径提高DOA估计精度.但该算法无法显著提高DOD估计精度,且只讨论了平面内的目标定位问题,没有充分利用EMVA中的多维角度信息.
针对双基地DOD和DOA估计问题,文章提出了一种新的EMVA-MIMO雷达系统.采用完备的EMVA阵元组成均匀矩形发射阵列,在MIMO雷达阵元间发射信号的正交约束条件下,还要求每个阵元的6个偶极子天线发射的信号相互正交,收发阵列几何结构相同.算法从输出数据中构造3阶测量张量,通过CP分解求取4维阵列流形矩阵、极化信息矩阵和多普勒矩阵.先借鉴ESPRIT算法从阵列流形矩阵中获取2维收发角的模糊估计.再根据目标极化散射模型,推导出极化信息矩阵的奇异值分解表达式,提出了一种通过该矩阵实现解模糊的算法,最终得到多目标2维DOD和DOA的高精度不模糊估计.该算法无需进行额外的参数配对,且通过扩展收发阵列孔径使得DOD和DOA估计性能均得到提高.
1 系统模型
双基地MIMO雷达的发射阵列为x-z平面内的均匀矩形阵列,由M=Mx×Mz个EMVA构成,其参考阵元位于x轴上,对第k个远场窄带目标的空间响应为

式中:λ表示信号波长;(·)T表示转置;ptk=[utk,vtk,wtk]T=[sinθtkcosφtk,sinθtksinφtk,cosθtk]T为第k个目标的方向余弦,φtk∈[0,2π)和θtk∈[0,π)是第k个目标的ADOD和EDOD;ti=[xi,yi,zi]T为第i个EMVA的坐标.每个EMVA包含3对电磁偶极子天线对,且相互正交放置于空间同一点,其响应为[12]

设 发 射 信 号 为S=[s1,…,sm,…,s6M]T∈C6M×L,且满足SSH=I6M,其中(·)H表示共轭转置,L为脉内采样点数,I6M为6 M维单位矩阵.第m路发射信号表示为时变向量的形式wm=,其中为式(2)中矩阵αptk的第i行,由天线的类型和朝向决定.则照射到第k个目标的信号为

ξH,ξV分别为发射波的两个正交极化分量,“⊗”为Kronecker积.设第k个目标的极化散射矩阵Ck恒定,在(H,V)基下表示为[13]

式中:chh,cvv为共极化系数;chv,chv为正交极化系数;参数a,b,c和d由散射点类型决定.接收阵列为y-z平面内均匀矩形阵列,由N=Ny×Nz个EMVA构成,其参考阵元位于y轴上,具有同式(1)和式(2)类似的响应αrk和αprk.则第q个脉冲的接收信号Xq=[x1,…,xn,…,x6N]T∈C6N×L可写成

复系数βk包含第q个脉冲内目标雷达截面积(Rada Cross-Section,RCS)信息和多普勒信息,Nq为零均值加性高斯白噪声.用Q个脉冲的匹配滤波输出数据构造矩阵Y=[y1,…,yQ],其中yq=vec(XqSH),vec(·)表示矩阵的列向量化.令E=[e1,…,eQ],其中eq=vec(NqSH),则

式中:“⊕”表示Khatri-Rao积;Β=[β1,…,βK],βk=[β1k,…,βQk]T∈CQ×1,在 目 标RCS满 足Swerling-I模型的条件下可从Β中获取目标多普勒频率[7];A=[α1,…,αK]∈CMN×K表示收发阵列的4维阵列流形矩阵,等同于相同几何结构下标量阵MIMO雷达收发阵列流形矩阵的Kronecker积,其列向量满足

Ap=[αp1,…,αpK]∈C36×K为极化信息矩阵,包含偶极子天线的响应与目标散射矩阵信息,由式(5)可得,其列向量满足

基于上述回波模型,提出一种从极化信息矩阵中得到目标二维收发角度不模糊估计的算法,将在2.2节中详细讨论.
2 角度估计算法
2.1 CP分解
为了从观测数据中得到目标角度和极化信息,在此引入CP分解算法.由式(5)和式(6)可得矩阵Y的任一元素可写成

式中[·]h,[·]i和[·]j分别表示对应向量的第h,i和j个元素.
定义1[14]:若张量为N个向量的外积,即张量的每个元素等于这N个向量相应元素的乘积,则X为秩1张量.
根据定义1将式(6)中矩阵Y构造成测量张量Y,使其等于K个秩1张量的和,有

“◦”表示向量外积.CP分解就是将张量Y分解成式(10)所示结构,从而得到因子矩阵的估计和.交替最小二乘算法(Alteranting Least Squares,ALS)可以利用3阶张量Y的3种模式展开矩阵Y(1),Y(2)和Y(3)求解CP分解问题,算法步骤可以参考文献[7]中相关内容.
Remark 1:当目标个数K满足2 K+2≤kA+kAp+kB的条件时,ALS算法得到的估计矩阵各列仅存在幅度和顺序上的模糊[14],其中kA,kAp和kB分别表示矩阵A,Ap和B的秩.当快拍数Q≥K时有kB=K,此时当目标数满足K≤MN+34时可以唯一分解出K个秩1张量.每个秩1张量仅包含对应目标的方向余弦信息,因此可以实现目标角度估计的自动配对.
2.2 二维收发角估计算法

其中arg[·]表示复数的幅角.同理可得wtk,vrk和wrk的估计.当阵元间距大于λ/2时,方向余弦存在周期性模糊.下面提出一种基于EMVA极化特性的解模糊算法.

式中,ui和vi分别为σi对应的左、右奇异向量.由式(2)易得和均为列满秩矩阵与Ck等秩.假设Ck满秩,则有2个非零奇异值,由式(12)可得

式中:gu1,gu2,gv1和gv2为未知复常数,且满足均为正实数;(·)*表示取复数的共轭;04表示4×4全零矩阵和分别组成矩阵和的零空间的标准正交基;即为秩等于2时的2个非零奇异值,且虑到矩阵Ck可能存在未满秩的情况,因此仅利用最大奇异值所对应的左、右奇异向量和估 计目标角度.将划分为两个3×1向量,由式(2)和式(13)可得


[·]i表示向量第i个元素.由式(2)和式(15)得

c3为未知实常数,不难得到



下面的表1中列出了算法的基本步骤:

表1 算法基本步骤
3 仿真实验
通过蒙特卡罗实验验证了本文算法的有效性,并与文献[7]和文献[11]中算法对比.本文的收发阵列为完备EMVA构成的2×3均匀矩形阵列.为保证可比性,文献[7]中收发阵列采用6×6均匀矩形标量阵列.文献[11]中发射阵列与文献[7]中发射阵列相同,接收阵列与本文接收阵列相同.7个远场不相关目标的参数如表2所示.快拍数均为100,噪声为独立零均值加性高斯白噪声,以所有目标角度估计均方根误差衡量算法性能,实验次数为100次.各图中实线、虚线和点画线分别表示本文算法、文献[7]算法和文献[11]算法的仿真数据,对应下标分别为v,s和sv.

表2 仿真目标参数
图1为3种MIMO雷达多目标DOD和DOA估计误差随信噪比变化曲线.空间中存在表2中的目标1~3,信噪比变化范围为[0dB,30dB],本文和文献[11]所用EMVA阵元间距为5λ,文献[7]和文献[11]中所用标量阵元的间距为λ/2.由图1(b)可知本文及文献[11]的算法扩展了接收阵列孔径,DOA估计精度大于标量阵MIMO雷达.在此基础上,本文算法还扩展了发射阵列孔径,由图1(a)可知本文算法可以获得更高的DOD估计精度,这一优势在低信噪比时仍然保持.
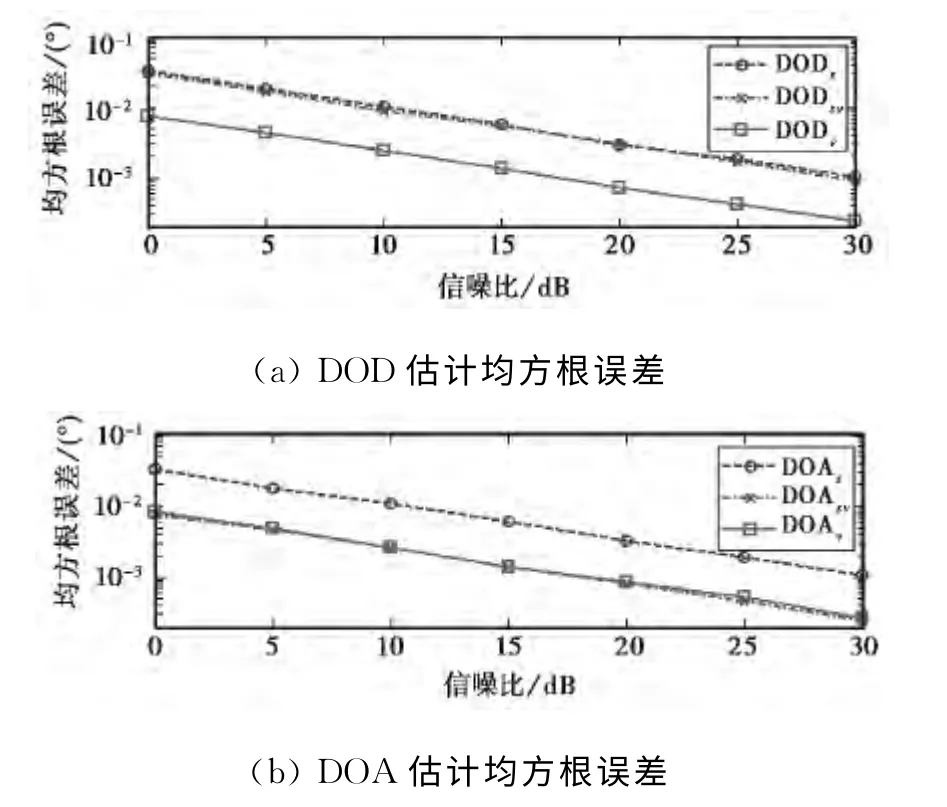
图1 估计误差与信噪比关系曲线
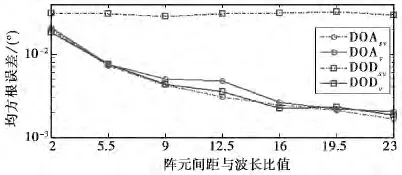
图2 估计误差与阵元间距关系曲线
图2为本文和文献[11]所提算法的角度估计误差随收发阵元间距变化的对比曲线.空间中存在表2中目标1~3,信噪比为0dB,所有EMVA阵元间距变化范围为[2λ,23λ],文献[11]发射阵列阵元间距为λ/2.由图2可知,文献[11]未能提高MIMO雷达的DOD估计性能,而本文算法在保证相同的DOA估计性能的情况下,DOD估计性能也得到了显著提升.
图3为MIMO雷达估计性能随目标个数变化的关系曲线.空间目标个数变化范围为[1,7],信噪比为0dB,标量阵元间距为λ/2,EMVA阵元间距为5λ.由图3可知,随着目标个数增多,本文所提算法的DOD估计误差上升幅度低于另两种MIMO雷达,DOA估计误差上升幅度低于标量阵MIMO雷达.

图3 估计误差与目标个数关系曲线
4 结 论
文章提出了一种收发阵列均采用EMVA技术的双基地MIMO雷达多维角度估计方法,给出了更严格的发射信号正交约束条件.首先利用经典算法(如ESPRIT算法)从张量分解后的4维阵列流形矩阵中估计出存在周期性模糊的目标角度,然后从目标极化散射矩阵出发分析了接收信号极化信息的构成,以此为基础推导了从极化信息矩阵中求解收发角的不模糊估计的算法,且实现了自动配对.仿真结果表明该算法在不同的信噪比和目标数条件下均具有良好的角度估计性能,且阵元间距无半波长限制,通过扩展孔径提高了参数估计精度.
[1]RABIDEAU D J,PARKER P.Ubiquitous MIMO multifunction digital array radar[C]//The Thirty-seventh Asilomar Conference on Signals,Systems and Computers,Pacific Grove,2003:1057-1064.
[2]曾建奎,何子述.慢起伏目标的多输入多输出雷达检测性能分析[J].电波科学学报,2008,23(1):158-161.ZENG Jiankui,HE Zishu.Analysis of MIMO detection performance for slow fluctuating target[J].Chinese Journal of Radio Science,2008,23(1):158-161.(in Chinese)
[3]程院兵,顾 红,苏卫民.双基地MIMO雷达发射波束形成与多目标定位[J].电波科学学报,2012,27(2):275-281.CHENG Yuanbing,GU Hong,SU Weimin.Transmit beamforming and multi-target localization in bistatic MIMO radar[J].Chinese Journal of Radio Science,2012,27(2):275-281.(in Chinese)
[4]陈显舟,杨 源,韩静静,等.双基地多入多出雷达收发方位角联合估计算法[J].电波科学学报.2013,28(1):176-182.CHEN Xianzhou,YANG Yuan,HAN Jingjing,et al.Joint DOD and DOA estimation using polynomial rooting for bistatic MIMO radar[J].Chinese Journal of Radio Science,2013,28(1):176-182.(in Chinese)
[5]JI L,CONAN J,PIERRE S.Joint Estimation of channel parameters for MIMO communication systems[C]//Second International Symposium on wireless Communication System,5-7September,2005:22-26.
[6]DUOFANG C,BAIXIAO C,GUODONG Q.Angle estimation using ESPRIT in MIMO radar[J].Electronics Letters,2008,44(12):770-771.
[7]YUANBING C,HONG G,WEIMIN S.Joint 4-D angle and Doppler shift estimation via tensor decomposition for MIMO array[J].IEEE Communications Letters,2012,16(6):917-920.
[8]NEHORAI A,TICHAVSKY P.Cross-product algorithms for source tracking using an EM vector sensor[J].IEEE Transactions on Signal Processing.1999,47(10):2863-2867.
[9]ZOLTOWSKI M D,WONG K T.ESPRIT-based 2-D direction finding with a sparse uniform array of electromagnetic vector sensors[J].IEEE Transactions on Signal Processing.2000,48(8):2195-2204.
[10]SVANTESSON T,JENSEN M A,Wallace J W.Analysis of electromagnetic field polarizations in multian-tenna systems[J].IEEE Transactions on Wireless Communications.2004,3(2):641-646.
[11]王克让,贺亚鹏,朱晓华.多输入多输出电磁矢量阵列雷达的DOD和DOA联合估计[J].航空学报.2011(2).WANG Kerang,HE Yapeng,ZHU Xiaohua.Joint DOD DOA and polarization estimation for MIMO radar with electromagnetic vector sensors[J].Journal of Electronics &Information Technology,2012,34(1):160-165.(in Chinese)
[12]GU C,HE J,LI H,et al.Target localization using MIMO electromagnetic vector array systems[J].Signal Processing,2013,93(7):2103-2107.
[13]WEI P S P,HUYNEN J R,BRADLEY T C.Transformation of polarisation bases for radar target scattering matrix[J].Electronics Letters,1986,22(1):13-14.
[14]KOLDA T G,BADER B W.Tensor decompositions and applications[J].Society for Industrial and Applied Mathematics.2009,51(3):455-500.
[15]NEHORAI A,PALDI E.Vector-sensor array processing for electromagnetic source localization[J].IEEE Transactions on Signal Processing,1994,42(2):376-398.

