一种分析多目标散射问题的区域分解方法

崔志伟 韩一平 于美平

（西安电子科技大学物理与光电工程学院，陕西 西安710071）

引 言

关于单个复杂目标的电磁散射问题已经有很多研究成果.然而实际中的许多目标并不是单独存在的，如自然界中的雨滴、阵列结构、军事编队等都是多个目标共同存在的.研究这些复杂多目标的电磁散射特性是一项基础又很有实用价值的工作，但是由于在计算过程中需要考虑多次散射，因此这又是一项难度很大的工作.近年来，随着计算机技术和数值计算技术的迅速发展，众多学者提出了用于分析多目标散射问题的各种不同的数值计算方法，如稀疏矩阵规则网格法［1］、特征基函数方法［2-3］、多层快速多极子方法［4-5］、多区迭代方法［6］、以及有限元区域分解方法［7］等.这些方法都有各自的优缺点，这里不进行评论，而是提出一种基于混合有限元-边界积分-特征基函数方法的新的区域分解方法.其基本思路是采用矢量有限元方法对每个目标进行分析，各个目标之间通过基于格林函数的边界积分方程进行耦合，所得到的耦合线性方程组采用基于Foldy-Lax多径散射方程的特征基函数方法进行求解［2-3，8-9］.

1 基本理论

待分析的多目标散射问题如图1所示.为了阐述问题方便，将自由空间所在区域记为Ω0，第i个目标所在的区域记为Ωi，相应的边界面为Si，其中i＝1，2，…，N，N为目标的个数.区域Ωi内的电场Ei满足下面泛函的变分［10］：

图1 多目标散射示意图

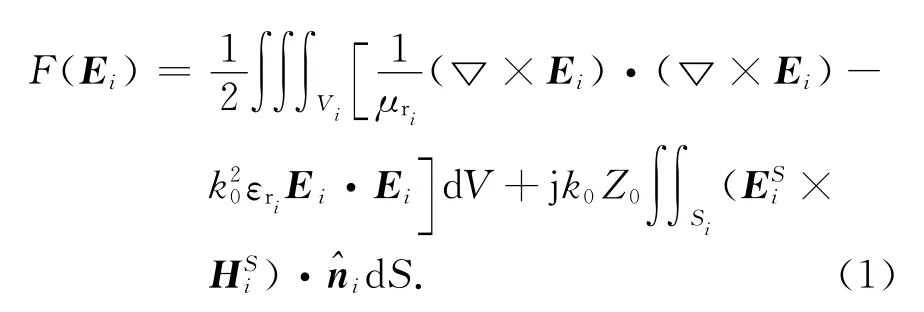
式中：Vi表示Si所包围的区域；表示边界Si的外法向单位矢量；εri和μri为第i个目标的相对介电常数和相对磁导率；k0和Z0是自由空间中的波数和波阻抗；和分别表示边界面Si上的电场和磁场.采用基于四面体单元的Whitney矢量基函数离散上述泛函得到［10］

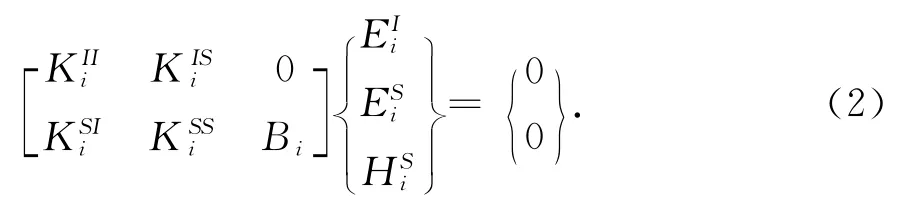
式中

对所有目标而言，边界面上的未知电场和未知磁场之间的关系可表示为

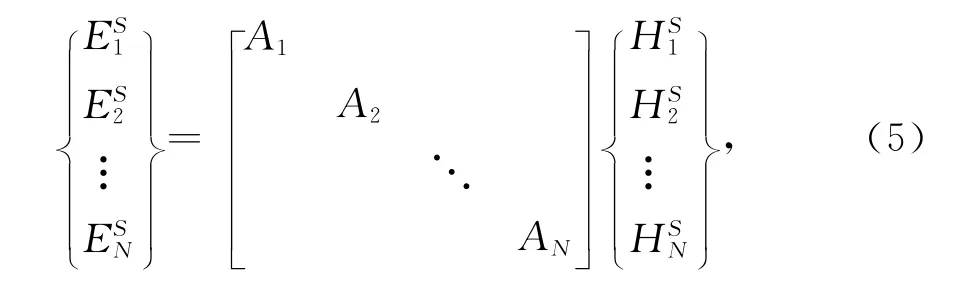
这里

如果所考虑的多个目标具有相同的形状与内部结构，则与各个目标相关的矩阵Ai是完全相同的，只计算与其中任何一个目标相关的Ai即可，这样可大大提高计算效率.为了能唯一地求解边界面上的未知电场和未知磁场，在边界面Si上引入等效电磁流源Ji和Mi，这组等效源满足

根据等效原理，在边界面Si上可建立如下的电场 积 分 方 程（Electric Field Integral Equation，EFIE）和磁场积分方程（Magnetic Field Integral Equation，MFIE）：

其中G0（r，r′）为自由空间中的格林函数.为了克服内谐振问题可将上面的电磁场积分方程联合得到如下的混合积分方程

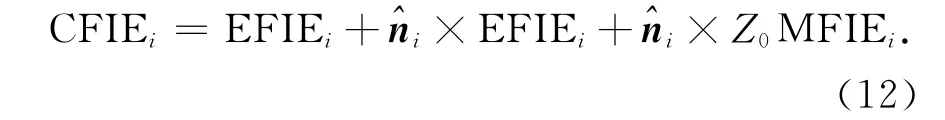
采用基于三角面元的RWG（Rao-Wilton-Glisson）基函数离散上述混合积分方程得到［11］

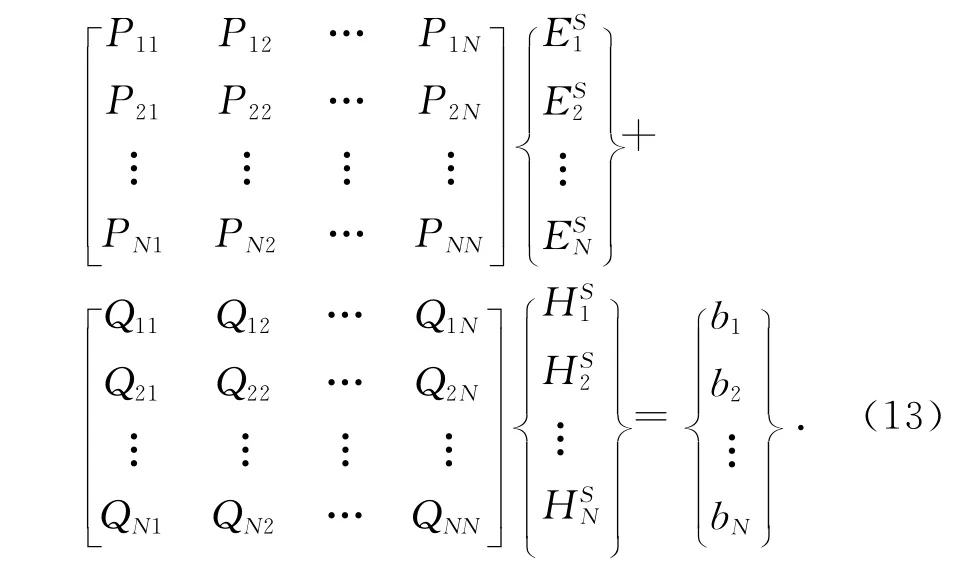
将式（5）代入式（13）得到

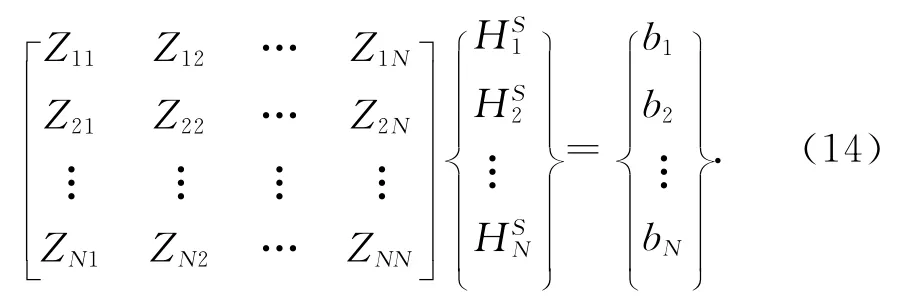
式中，Zij＝PijAi＋Qij（i，j＝1，2，…，N）.对此方程的求解，可以采用文献［2］中提出的特征基函数方法.在该方法中，特征基函数根据Foldy-Lax多径散射方程构造，即第个i目标最终的激励场等于入射场加上除此目标之外其他所有目标的散射场.每个目标初次特征基函数的激励场为初始的入射场，初次特征基函数的建立忽略了所有本目标与其他目标间的互耦.而一阶高次特征基函数是通过将所有其他目标的初次特征基函数产生的散射场代替入射场后计算出来的.类似地，可计算出其他的更高次的特征基函数.所构造的特征基函数可以有效的降低阻抗矩阵的尺度，从而可以使用直接法而不需要使用迭代来求解积分方程离散后的矩阵方程，具体的求解过程见文献［2］.

需要指出的是，由于矢量有限元方法的灵活性，本文提出的区域分解方法既适用于多个均匀目标，也适用于多个非均匀目标，同时还适用于多个各向异性目标，尤其适合于求解多个具有相同结构目标的散射问题.

2 数值结果

为了验证公式和程序的正确性，首先考虑2×2×2的阵列均匀各向同性介质球，每个球的半径为r＝0.2λ，相对介电常数和磁导率分别为εr＝2.0和μr＝1.0，在x，y方向上的周期为T＝2.0λ.图2给出了该阵列均匀各向同性介质球的双站雷达散射截面（Radar Cross-Section，RCS），并将本文的数值结果和广义多球米理论的解析解进行了对比.从图中可以看出，两者吻合很好.

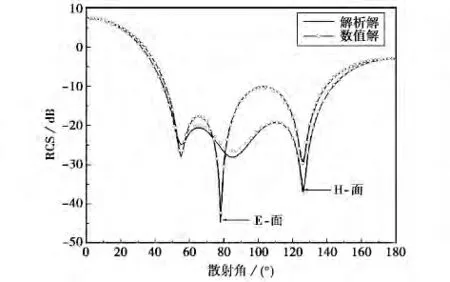
图2 2×2×2阵列均匀各向同性介质球的RCS

为了说明该方法处理复杂多目标散射问题的能力，下面给出三个算例.第一个算例考虑的是2×2的阵列均匀各向异性介质球，每个球的半径为r＝0.5λ，在x，y方向上的周期为T＝0.2λ.相对磁导率分别μr＝1.0，相对介电常数为

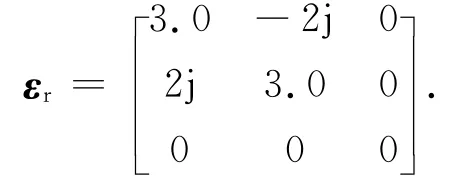
图3给出了该阵列均匀各向异性介质球的RCS.

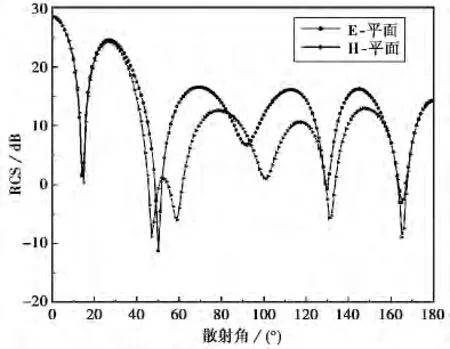
图3 2×2阵列均匀各向异性介质球的RCS

第二个算例考虑的是8×8的阵列介质涂层导体圆柱，每个导体圆柱的半径和高分别为r＝0.5λ和h＝1.0λ，介质涂层的厚度为t＝0.1λ，相对介电常数和磁导率分别为εr＝2.0和μr＝1.0，在x，y方向上的周期为T＝2.0λ.图4给出了该阵列圆柱的RCS.

最后一个算例考虑的是采用蒙特卡罗方法模拟的1 000个随机离散均匀介质球形粒子的散射，如图5所示.其中每个小球的半径为r＝50nm，复折射率为m＝1.6-j0.6，占空比为f＝10%，入射平面波的波长为λ＝532nm.图6给出了这些随机离散球形粒子的RCS.

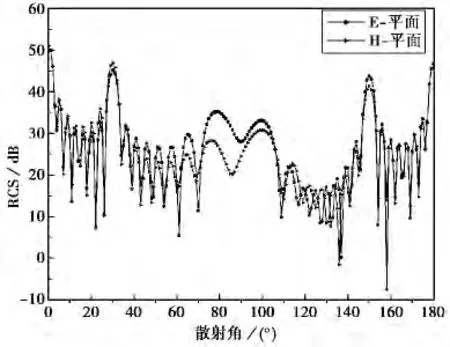
图4 8×8阵列介质涂层导体圆柱的RCS

图5 采用蒙特卡罗方法模拟的1 000个随机离散粒子分布图

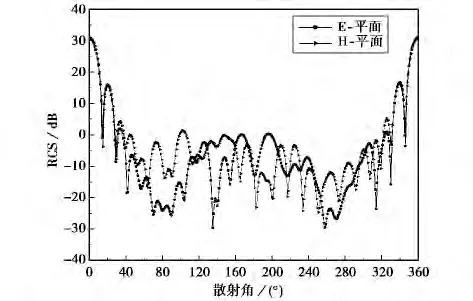
图6 1 000个随机离散均匀介质球形粒子的RCS

3 结 论

针对多目标散射问题，本文提出了一种基于混合有限元-边界积分-特征基函数方法的区域分解方法.该方法采用矢量有限元方法对每个目标进行分析，并通过高斯消去法把求解区域内部未知量的问题转化为求解边界面上未知量的问题；各个区域之间通过基于格林函数的边界积分方程进行耦合；所得到的耦合矩阵方程采用基于Foldy-Lax多径散射方程的特征基函数方法进行求解.该方法既适用于多个均匀目标，也适用于多个非均匀目标，同时还适用于多个各向异性目标.文中给出的数值结果证明了这种方法的准确性和处理复杂多目标散射问题的能力.

［1］CHAN C H，TSANG L.A sparse-matrix canonicalgrid method for scattering by many scatterers［J］.Microwave and Optical Technology Letters，1995，8（2）：114-118.

［2］SUN Y F，CHAN C H，MITTRA R，et al.Characteristic basis function method for solving large problem arising in dense medium scattering［C］／／IEEE Antennas and Propagation Society International Symposium.Columbus，June 22-27，2003：1068-1071.

［3］孙玉发，张 奕，徐善驾，等.二维多导体柱电磁散射特性的特征基函数法分析［J］.电波科学学报，2006，21（2）：229-232.SUN Yufa，ZHANG Yi，XU Shanjia，et al.EM scattering analysis of 2-D multiple conducting cylinders using characteristic basis function method［J］.Chinese Journal of Radio Science，2006，21（2）：229-232.（in Chinese）

［4］LI L，HE J Q，LIU Z J，et al.MLFMA analysis of scattering from multiple targets in the presence of a half-space［J］.IEEE Transactions on Antennas and Propagation，2003，51（4）：810-819.

［5］RUI X，HU J，NIE Z P.Solving scattering from multiple conducting objects by hybrid multi-level fast multi-pole algorithm with generalized forward-andbackward method［J］.Electromagnetics，2008，28（8）：572-581.

［6］芮 锡，胡 俊，聂在平.基于多区迭代的多导体目标散射分析［J］.系统工程与电子技术，2008，30（11）：2116-2118.RUI Xi，HU Jun，NIE Zaiping.Electromagnetic scattering analysis of multipole conductor by multiregion iterative method［J］.Systems Engineering and Electronics，2008，30（11）：2116-2118.（in Chinese）

［7］ZHAO K Z，RAWAT V，LEE J F.A domain decomposition method for electromagnetic radiation and scattering analysis of multi-target problems［J］.IEEETransactions on Antennas and Propagation，2008，56（8）：2211-2221.

［8］孙玉发，卢 克，王国华.介质目标电磁散射特性的多层特征基函数法分析［J］.电波科学学报，2013，28（1）：92-95.SUN Yufa，LU Ke，WANG Guohua.Analysis of electromagnetic scattering characteristics from dielectric objects using multilevel characteristic basis function method［J］.Chinese Journal of Radio Science，2013，28（1）：92-95.（in Chinese）

［9］王国华，孙玉发，于君之.特征基函数法快速分析导体目标电磁散射特性［J］.电波科学学报，2013，28（3）：438-442.WANG Guohua，SUN Yufa，YU Junzhi.Fast analysis on electromagnetic scattering characteristics of conducting targets using characteristic basis function method［J］.Chinese Journal of Radio Science，2013，28（3）：438-442.（in Chinese）

［10］盛新庆.计算电磁学要论［M］.2版.合肥：中国科学技术大学出版社，2008.

［11］CUI Z W，HAN Y P，Zhao W J.Scattering of arbitrarily incident Gaussian beams by fractal soot aggregates［J］.Journal of Optics A：Pure and Applied Optics，2012，14（3）：035703.