求解多尺度目标电磁散射的积分方程快速算法

郑宇腾 赵延文 贾苗苗 蔡强明 聂在平

（电子科技大学电子工程学院，四川 成都611731）

引 言

基于频域表面电场积分方程（Electric Field Integral Equation，EFIE）的矩量法可用于许多电磁问题的求解.然而由于传统矩量法的计算复杂度高，对于大未知量问题需要采用快速算法以降低计算复杂度.多层快速卡特森展开算法（Multilevel Accelerated Cartesian Expansion Algorithm，MLACEA）［1］是一种更适合于模拟电小尺寸目标电磁散射／辐射问题的快速算法.该算法与多层快速多极子算法（Multilevel Fast Multipole Algorithm，MLFMA）［2-4］相似，采用了基于八叉树结构对基函数进行分组，将矩矢相乘分解为聚合、转移、配置的三个过程以降低计算复杂度；而不同之处在于采用了卡特森张量来展开格林函数［5-6］.卡特森张量展开是三元函数泰勒展开的张量表达形式，适用于小宗量的函数展开，并可通过调整张量的阶数来控制展开精度.对于电大目标的电磁问题，由于格林函数的宗量较大该方法无法求解.

另一方面，在传统的MLFMA算法中，对于含有精细结构的电大目标的电磁散射／辐射问题，为避免快速算法的低频不稳定现象［7］，MLFMA算法的最细层分组大小一般要求不能小于0.25个波长.这样，在目标被精细剖分（如低频问题或具有精细结构）的情况下，MLFMA算法的单个分组内未知量数目会显著上升、导致计算量及内存开销增大.因而，若采用MLFMA算法与MLACEA算法的混合算法可大幅度降低求解多尺度问题的计算复杂度［8］.

1 多层快速卡特森展开算法

假设S为位于均匀背景介质（通常选取为自由空间）中的理想导体表面，入射电场为Einc（r）.利用导体表面上切向电场所满足的边界条件，可得到理想导体表面S上感应电流J（r）所满足的混合位电场积分方程，

而标量格林函数G（r，r′）为

式中

为了降低电场积分方程矩量法的计算复杂度，可采用MLACEA及其与MLFMA的混合算法MLACEA-MLFMA算法，该算法基于八叉树结构对目标进行多层递推分组.最细层分组盒子边长可按照实际需求（如最细层分组内的平均未知量数目等）设置，算法不会出现低频不稳定问题，更适合于求解包括含精细结构的多尺度目标电磁散射／辐射问题.

利用卡特森张量可将任意标量函数ψ（r-r′）展开为

式中，▽（q）表示关于r的q次复合梯度算子，它将所作用的标量函数映射成为一个q阶张量函数.而A（p＋q）·q·B（q）则表示张量A（p＋q）与张量B（q）之间的张量压缩运算，张量r′（q）以及张量▽（q）G（r，r′）均为完全对称张量.

式中，Anear、Φnear和Afar、Φfar分别表示对应于标量位和矢量位的近区及远区场源组对之间的阻抗矩阵.利用（9）可以将远区场源组对对矩阵与矢量乘积的贡献）表示为

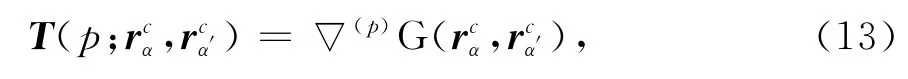
而标量位对应的聚合因子、配置因子及聚合量分别为

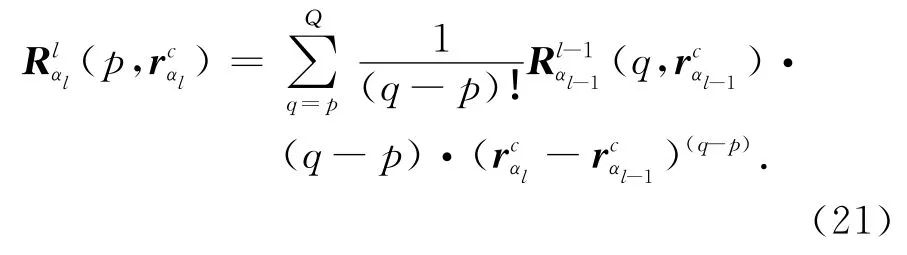
2 MLACEA-MLFMA混合算法

在MLFMA算法中，远区组作用对矩矢相乘的贡献Vfar可以表示为

而快速多极子的配置因子

设映射张量Tmap（p·R）为，

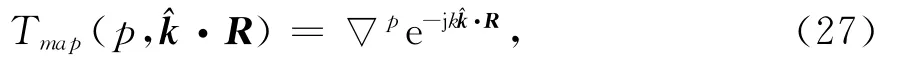
在此基础上再结合MLFMA的递推公式（21）～（22），即可构建完整的MLACEA-MLFMA混合算法.

3 数值计算结果

通过数值算例来对比分析混合算法的精度与计算效率.计算平台采用Intel Core-i5处理器，主频3.0GHz，内存8GB，采用单精度浮点数计算.在以下各例子中，矩阵方程均采用收敛门限为0.01的广义最小残差迭代法求解.

第一个实例为半径为1.5个波长的理想导体球，基函数总数为12.8万.入射波沿＋z方向传播、电场极化沿x轴方向.采用3层的MLFMA算法、而MLACEA-MLFMA混合算法则是在MLFMA算法基础上再细分一层，且MLACEA算法采用4阶卡特森张量展开.表1对比了MLFMA算法和MLACEA-MLFMA混合算法的计算复杂度，图1对比分析了MLFMA算法和MLACEA-MLFMA混合算法所计算的双站雷达散射截面积.由表1和图1可以看出，与单独采用MLFMA算法相比，混合算法显著地降低了内存需求，加快了附近组的阻抗矩阵填充和矩阵与矢量乘积的计算速度.

表1 MLFMA与MLACEA-MLFMA的计算复杂度对比

图1 两种方法计算理想导体球双站雷达散射截面积结果对比

第二个例子结合实际应用，以载体天线阵列一体化模型的散射计算作为实例.载体及天线单元尺寸如图2所示，天线阵列为8×8的Vivaldi天线阵.由于天线阵列较载体的复杂程度高，因而在剖分时对载体采用边长约为0.125稀疏网格剖分出11 722个三角单元，而对天线以边长约为0.025λ的高密度网格剖分出21 750个三角单元，总未知量为48 963.平面波传播方向平行于xoz面，与＋z轴夹角θ＝135°，电场极化沿y轴方向.从表2统计的计算开销对比可以看出，MLACEA-MLFMA通过细分底层盒子，减少了近区组元素，因而在近区组阻抗矩阵的计算时间与总内存消耗上都远远小于MLFMA方法.另外，对比前一算例可以看出，多尺度网格对近区组计算时间及内存开销的影响相当剧烈.图3的双站雷达散射截面积对比可以反应出，混合形式的快速算法在计算实际工程问题时依然能够具有与MLFMA方法相当的计算精度.并且为提高矩阵矢量相乘的计算效率，该算例虽仅采用了3阶的卡特森张量展开，但依然能保证计算结果的准确性.

图2 车载天线阵列模型示意图

表2 MLFMA与MLACEA-MLFMA的计算复杂度对比

图3 两种方法计算车载天线阵列模型双站雷达散射截面积结果对比

4 结 论

详细阐述了多层快速卡特森展开算法（MLACEA）及其与多层快速多级子算法（MLFMA）的混合算法MLACEA-MLFMA.MLACEA算法大幅度降低了精细剖分网格条件下积分方程矩量法的计算复杂度；而MLACEA-MLFMA混合算法能够更高效地模拟含精细结构的电大尺寸目标（宽带）电磁散射及辐射问题.

［1］HANKER B，and Huang H.Accelerated Cartesian expansions-a fast method for computing of potential of the form r-νfor all realν［J］.Journal of Computational Physics，2007，226（1）：732-753.

［2］SONG J，LU C and CHEW W C.Multilevel fast multipole algorithm for electromagnetic scattering by large complex objects［J］.IEEE Transaction on Antenna and Propagation，1997，45（10）：1488-1493.

［3］胡 俊，聂在平，王 军，等.三维电大目标散射求解的多层快速多极子方法［J］.电波科学学报，2004，19（5）：509-514.HU Jun，NIE Zaiping，WANG Jun，et al.Multilevel fast multipole algorithmfor solving scattering from 3 D electrically large object［J］.Chinese Journal of Radio Science，2004，19（5）：509-514.（in Chinese）

［4］潘小敏，盛新庆.电特大复杂目标电磁特性的高效精确并行计算［J］.电波科学学报，2008，23（5）：888-893.PAN Xiaomin，SHENG Xinqing.Efficient and accurate parallel computation of electromagnetic scattering by extremely large targets［J］.Chinese Journal of Radio Science，2008，23（5）：888-893.（in Chinese）

［5］APPLEQUIST J.Cartesian polytensors［J］.Journal of Mathmatic and Physics，1983，24（4）：736-742.

［6］APPLEQUIST J.Traceless cartesian tensor forms for spherical harmonic functions：new theorems and applications to electrostatics of dielectric media［J］.J Phys A：Math Gen，1989，22（20）：4303-4330.

［7］ZHAO J S，CHEW W C.Applying LF-MLFMA to solve complex PEC structures［J］，Microwave and Optical Technology Letters，2001，28（3）：155-160.

［8］VIKRAM M，HUANG H，SHANKER B，et al.A novel wideband FMM for fast integral equation solution of multiscale problems in electromagnetics［J］.IEEE Transaction on Antenna and Propagation，2009，57（7）：2094-2104.