基于能量法的车辆稳定性判断研究*

罗玉涛，来恩铭

(华南理工大学机械与汽车工程学院，广东省汽车工程重点实验室，广州 510640)

前言

目前，国内外操纵稳定性控制的失稳判断常用的方法有质心侧偏角的相平面法。比较成熟的车辆稳定性控制系统主要有博世的ESP等。博世的ESP系统是一个状态反馈控制器，其中状态变量为汽车的质心侧偏角与横摆角速度，且车辆的质心侧偏角的控制权值随着侧偏角的增大而增大。对带有独立四轮车辆模型的动力学方程进行线性化，采用了黎卡提线性二次最优控制方法设计控制器，控制器的输入信号为通过2自由度模型估算得到的理想质心侧偏角和横摆角速度与实际值之间的差值。状态控制器的输出为需求的横摆力矩[1]。德国大陆公司提出一种可以区分不同驾驶工况的控制仲裁器。基于车辆不同的行驶工况(部分制动工况、全力制动工况、驱动工况和四轮驱动工况)和车辆失稳转向倾向(过度转向和不足转向)，其中对横摆角速度、质心侧偏角偏差采用PID控制，同时对车辆车轮制动力与发动机转矩进行了相应的控制，并与ABS、TCS系统进行相应的协调控制[2]。Mando公司则是基于理想横摆角速度和实际横摆角速度的偏差，采用PID控制估算车辆所需的补偿横摆力矩，并计算相应制动轮的滑移率，通过车辆滑移率模块对车轮进行主动制动和介入发动机管理系统对发动机转矩进行控制，使得车辆处于稳定状态[3]。

车辆稳定性控制系统中的一个关键部分就是对车辆的行驶稳定性进行判断。目前常用来表征车辆行驶稳定性状态的参数是车辆的横摆角速度和质心侧偏角[4-9]。因此可以通过比较横摆角速度和质心侧偏角的实际值与理想值之间的差值确定出车辆行驶状态。当两者的差值较小时，可认为车辆处于稳定状态，无需稳定性控制系统的介入；若两者差值过大，说明车辆处于不稳定状态，需要车辆稳定性控制系统的介入，使车辆保持行驶稳定。但车辆的质心侧偏角不像横摆角速度那样可以直接测得，因此有必要研究并设计用于车辆的稳定性的新的判断方法。

本文中提出了一种基于能量法的车辆稳定性判断方法。将车辆的侧向运动动能与横摆动能之和定义为失稳动能。通过建立失稳动能与纵向运动动能的比值及其变化率来表征车辆的行驶稳定性。在汽车行驶过程中，希望在各种行驶条件下，车辆的失稳动能与纵向运动的动能的比值保持在一定的可控范围内。若侧向运动的动能过大，则会引起能量比变大，从而使车辆失去稳定性。因此本文中根据相平面法设计了基于失稳能量比的车辆稳定性判断式。在Vedyna软件中进行车辆的双移线仿真分析，证明了该稳定性判断的有效性。

1 车辆的动力学模型

图1为汽车运动受力简图。选用常用的坐标系，即x轴指向车辆前进方向；y轴指向车辆左侧；z轴按右手定则，垂直向上。对于简化的汽车模型而言，具有纵向位移、横向位移、横摆角速度3个方向的整车运动和4个车轮的回转运动。

根据图1可以得到车辆运动基本方程。

纵向动力学方程为

(1)

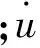
侧向动力学方程为

(2)

横摆运动方程为

(3)

式中：Iz为车辆绕z轴的转动惯量；df为前轮距；dr为后轮距；lf为质心到前轴之间的水平投影距离；lr为质心到后轴之间的水平投影距离。

由于轮胎的侧向力很难测量，因此本文中采用了HSRI轮胎模型[10]进行估算：

(4)

(5)

(6)

由式(4)和式(5)可推导出轮胎的侧向力和纵向力具有关系：

(7)

式中：Cx为轮胎滑移刚度；Cy为轮胎侧偏刚度；λ为轮胎的滑移率；α为轮胎的侧偏角；FN为轮胎的法向力；μ为轮胎与路面之间的最大的附着系数。

2 车辆稳定性判断

2.1 失稳能量比的定义

车辆的稳定性判断是稳定性控制策略的基础。汽车在正常路面上行驶经常需要转弯或受到侧向风的影响。当轮胎的侧向力接近饱和时，轮胎与路面之间的侧向力将不再与轮胎侧偏角成线性关系。

车辆在行驶过程中其总动能可以分解为前轴质量动能ETf和后轴质量动能ETr[11]，其中每项包括平动动能和转动动能项。前、后轴的动能ETf和ETr分别为

(8)

(9)

其中：uf=ur=u；vf=v+lfωr；vr=v-lrωr

式中：mf、mr分别为等效至前、后轴的车辆前半部和后半部的质量;Izf和Izr分别为车辆前半部和后半部绕z轴的转动惯量;uf、ur分别为前后轮的纵向速度;vf、vr分别为前后轮的侧向速度。

车辆的纵向运动动能为

(10)

车辆的失稳动能为

(11)

因为正常行驶中车辆的横摆角速度非常小，假设车辆的横摆角速度不高于0.2rad/s，车辆的时速为60km/h，通过估算可知一般车辆的横摆能量小于车辆的平动动能的0.1‰。当行驶中的车辆出现较大的横摆运动时，横摆角速度可以侦测到车辆的运动，并进行干预，同时车辆较大的横摆运动也会间接影响车辆的侧向和纵向速度。

因此，车辆的横摆角速度引起的能量相对于侧向动能基本可以忽略。

综上所述，定义失稳能量比为

(12)

当失稳能量比越大，则表示侧向运动与横摆运动的成分越多。在直线行驶中，驾驶员希望失稳能量比尽可能接近零。

2.2 能量比的特性分析

在车辆稳定性控制中，车辆的行驶稳定性非常重要。车辆失去稳定则表征着很难恢复到稳定区域，因此正常情况下不允许出现过大的能量比。当估算能量比较小时，若车辆不出现失稳，系统可以不施加控制。若能量比过大时，控制系统则需要通过间接控制来抑制这种能量比绝对值增大的趋势，使其接近理想值。相平面法可对这一类非线性问题进行分析研究。结果表明，在实际控制中，只要相轨迹在稳定的区域内，在扰动存在的情况下，轨迹会自动收敛至稳定的焦点。当轨迹处于不稳定的区域时，控制系统对能量比进行间接控制，通过施加控制使其回到稳定区域。

能量比也间接影响着车轮的侧偏角，简化模型的前后轮侧偏角与能量比的关系为

(13)

(14)

式中：αf、αr分别为前后轮的侧偏角(忽略左右轮侧偏角的差别，αfl=αfr=αf,αrl=αrr=αr);δ为前轮转向角。

因此，将前后轮侧偏角代入轮胎模型中估算轮胎力和横摆力矩，得到如图2所示的关系图，车辆在一定的稳态转向时，车辆横摆力矩与能量比之间的关系曲线。

由图2分析可知，当能量比较小时，横摆力矩与能量比处于线性区域，近似成正比；随着能量比的增大，横摆力矩在某一能量比时开始减少，并趋于稳定值，此时即使是有经验的驾驶员也很难通过操纵转向盘来有效控制车辆。引起这种现象的原因主要是由于后轮侧偏特性进入了非线性饱和区域所导致的。车辆前轮的侧偏特性对横摆力矩的影响不大。随着能量比的增大，横摆力矩的减少主要是由于后轮侧偏特性趋于饱和所导致的。所以，在低附着路面上应该严格限制车辆的失稳动能与纵向运动动能的能量比，才能使车辆保持稳定。

由于轮胎侧偏特性的影响，在图2中，当能量比较大时，轮胎的侧向力将趋于饱和，使得车辆的横摆力矩也趋于饱和。由于前后轴侧向力处于饱和状态，对质心的横摆力矩不能够抵消，所以当能量比增大时，横摆力矩将偏离M=0。当斜率为正时，车辆表现出一定的不足转向特性。当斜率为负时，车辆就表现为一定的过多转向特性，此时若车速超过车辆的极限车速，则会导致车辆失稳。车辆在加速过程中横摆力矩将会增大，由于轮胎的载荷向后转移，车辆将表现出很强的不足转向特性。过量的不足转向和过度转向都会导致车辆失去稳定性。因此，可以将失稳能量比作为车辆稳定性控制系统的一个重要的控制量。

2.3 稳定性判断准则

相平面法是一种求解常微分方程的图解方法，其实质是将系统的动态过程在相平面内用运动轨迹的形式绘制成相平面。根据相平面图全局的几何特性，判断系统所固有的特性。本文中利用失稳能量比作为横坐标，将失稳能量比变化率作为纵坐标。在能量比与能量比变化率相图中存在一个稳定区域，在该区域内，从任意初始点出发的相轨迹最终都收敛于稳定的焦点，即车辆能恢复到相应的稳定状态。同时由于车辆稳定域由奇点近似界定，分析奇点也可以分析车辆稳定性的变化[12]。

综上所述，建立失稳能量比的相平面法判断汽车的失稳状态，采用如下稳定性判定准则：

(15)

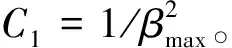
3 仿真计算与结果分析

以某车辆为例，在Vedyna软件中建立该车辆的动力学模型。该车辆的整备质量为1 435kg，轴距为2 710mm。确定判别式中的参数C1、C2，在大侧偏角下，当转向盘转角改变时，横摆力矩几乎不发生变化，特别是在物理极限条件下，在较好的路面条件下，物理极限的质心侧偏角约为12°，横摆角速度约为22°/s，将车辆的极限质心侧偏角与横摆角速度带入方程中求解：C1=19.36，C2=6.76。因此，稳定性判断准则曲线如图3所示。

由图3可知，当车辆行驶过程中失稳能量比与能量比变化率的坐标点落在两条直线之间，则认为车辆此时处于稳定状态，没有发生失稳现象；反之则认为车辆出现了失稳，此时稳定性控制系统对车辆进行主动干预。

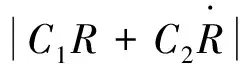
分析图4可知，当7.6s时稳定性判断式计算结果大于1时，此时车辆出现了失稳现象。观察无稳定性控制系统时，车辆在该时刻的质心侧偏角。从质心侧偏角观测数据可知，在7.6s时车辆即开始产生了较大的质心侧偏角，并伴随着不断增大的趋势，说明此时车辆已经发生了较明显的侧偏，失去了行驶稳定性。其中失稳程度越严重，判据式的计算结果也越大，进一步证明该稳定性判据的有效性。

图6为车辆加装了稳定性控制系统后的稳定性判断式计算结果。对比图4的计算结果可知，当系统判断7.6s时车辆失稳，稳定性控制系统进行干预。稳定性判断式计算结果在该稳定性控制系统多次介入下大幅减小，并且最终小于1趋于0，使车辆进入稳定区域。

假设车辆在高附着路面行驶，其中路面附着系数为0.8，车辆的行驶车速为80km/h，进行车辆的双移线仿真实验，仿真结果如图7和图8所示。

由图7可知，当路面附着系数为0.8时，计算的稳定性判断结果均小于1，对比此时车辆的质心侧偏角，可知行驶过程中车辆的质心侧偏角始终较小，因此车辆并没有发生失稳现象，稳定性判定准则也有效地跟踪了车辆的行驶状态。

综上所述，当车辆在低附着路面和高附着路面时，稳定性判断准则都能有效地表征车辆的行驶稳定性状态。

4 结论

本文中针对汽车的操纵稳定性控制系统中车辆的失稳判断进行详细研究。通过能量法建立车辆的失稳动能与纵向运动动能，并将两者的比值定义为失稳能量比，结合相平面法设计了车辆行驶过程中的稳定性判断准则，识别车辆的行驶状态。最后在Vedyna仿真分析软件下对车辆在高附着路面和低附着路面进行了双移线仿真分析。结果表明，当车辆在高、低附着路面时，稳定性判断准则都能有效地表征车辆的行驶稳定状态。

[1] Anton T Van Zanten,Rainer Erhardt,Klaus Landesfeind,et al.VDC Systems Development and Perspective [C].SAE Paper 980235.

[2] 陈帧福.ESC 的工作原理与发展前景 [R].法兰克福: 德国大陆公司,2007.

[3] Kim Dongshin,Kim Kwangil,Lee Woogab,et al.Development of Mando ESP(Electronic Stability Program) [C].SAE Paper 2003-01-0101.

[4] 程军.车辆动力学控制的模拟[J].汽车工程，1999,21(4)：199-205.

[5] 王德平,郭孔辉,宗长富.车辆动力学稳定性控制的仿真研究[J].汽车技术，1999,2:8-10.

[6] A T Van Zanten.Bosch ESP System:5 Year of Experience[C].SAE Paper 2000-01-1633.

[7] Tseng H E,et al.Technical Challenges in The Development of Vehicle Stability Control System[C].IEEE,1999.

[8] Yoshiki Fukada.Slip-Angle Estimation for Vehicle Stability Control[J].Vehicle System Dynamics,1999,32:375-388.

[9] Hideaki Sasaki,Takatoshi Nishimaki.A Side-slip Angle Estimation Using Neural Network for a Wheeled Vehicle[C].SAE Paper 2000-01-0695.

[10] Van Zanten,et al.Control Aspects of the Bosch-VDC,AVEC’96[C].International Symposium on Advanced Vehicle Control,Aachen,June 24-28,1996: 576-607.

[11] 喻凡，林逸.汽车系统动力学[M].北京：机械工业出版社，2005.

[12] 盖玉先,等.汽车动力学稳定性的研究[J].哈尔滨工业大学学报，2006(12):12-17.