关于缸压传感器替代发动机凸轮轴和曲轴位置传感器的研究*

王金力,杨福源,欧阳明高,黄 颖,方 成,2,杨学青

(1.清华大学汽车工程系,北京 100084；2.北京易控凌博汽车电子技术有限公司,北京 100084)

前言

缸压信号作为反映发动机工作状况的最直接的信号，一直以来都是研究的热点[1-6]。由于技术的限制，缸压传感器的成本一直很高，因而其应用一直停留在试验阶段。近年来随着技术的发展，压阻式缸压传感器目前已经实现了在量产车型中的应用。其中Insignia 2009款车型就加装了PSG型缸压传感器[7]，该车型被美国《Motor Trend》杂志评选为2009年度车型。可以预见，随着技术的不断进步，缸压传感器的价格会越来越低，而且HCCI新型燃烧方式等前沿技术的兴起，也为缸压传感器在更大范围内发挥作用提供了舞台[8-10]。

缸内压力信号包含丰富信息，能反映缸内气体压缩过程、燃烧放热过程和膨胀做功过程，与曲轴位置信息结合，可以解析出放热始点、最大缸压及其位置、5%燃烧放热率位置和50%燃烧放热率位置等等，多个缸压信号可以解析出上述指标的缸间差异。因此，基于缸压实时监测的发动机燃烧过程闭环控制正成为研究热点[11-15]，基于缸压的燃烧闭环电子控制平台正在形成。

凸轮轴和曲轴信号所提供的相位基准是传统发动机控制体系的基础。凸轮轴信号的主要作用是判定第1缸的压缩上止点，因此凸轮轴位置传感器又被称为气缸识别传感器(cylinder identification sensor,CIS)。它通常通过缺齿或者多齿来实现这一功能，因而能提供一定的相位信息。曲轴信号的主要作用是提供更精确的相位信息和生成用于控制与诊断的转速信息。

在传统燃油喷射控制体系中[16]，如果凸轮轴信号丢失，通常通过试喷的策略来识别气缸。这种策略算法比较复杂，在冷起动的情况下其可靠性也较难保证，而且会产生不必要的燃油消耗。如果曲轴信号丢失，则只能依靠凸轮轴信号所提供的较低的角度分辨率来确立其相位基准。此时，喷油定时的控制精度，以至于发动机转矩、油耗和排放等性能都会受到影响。由于这两种情况下，发动机仍有可能以非正常状态工作，为发动机“跛行回家”提供条件，这两种控制通常也被称为跛行回家功能。

本文中通过理论与试验相结合，探讨用缸压传感器替代凸轮轴和曲轴传感器的可行性，具体包括基于缸压信号的发动机气缸识别、相位估计和转速估计的理论分析与建模和燃烧解析单元的开发与试验评估。

1 理论基础与建模

1.1 基于缸压信号的气缸识别

当发动机位于压缩上止点时，封闭气体经压缩后，压力明显升高；当发动机位于进、排气上止点时，缸内压力与进气压力位于同一数量级，变化十分平缓。根据气缸压力这一特征即可实现气缸识别。

1.2 基于缸压信号的曲轴相位估计

基于缸压信号进行曲轴相位估计针对的缸压是燃烧放热之前的缸压(严格地讲是燃油喷射之前)，即倒拖缸压信号。相位估计分为两个步骤：(1)确定缸内压力与气缸容积的关系;(2)确定气缸容积与曲轴相位之间的关系，其公式为

(1)

式中：V(φ)为对应曲轴转角为φ时的气缸总容积；Vc为活塞在上止点时的气缸容积；d为气缸直径；r为曲柄半径；l为连杆长度。下面给出3种估计模型。

1.2.1 理想气体压缩模型

在压缩冲程中，忽略气体泄漏损失和缸壁传热损失，将缸内气体视为理想气体，则有

pVκ=const

(2)

式中：p为缸内压力；V为气缸容积；κ为绝热指数。部分文献根据缸内气体温度对κ进行一定程度的修正[17-19],本文中将κ取为固定值。以压缩冲程始点为参考点，有

(3)

1.2.2 简单漏气模型

根据理想气体状态方程：pV=nRT，发动机的有效压缩比与活塞环漏气损失对气体摩尔数n和缸壁传热损失对温度T的影响，都会影响到缸内压力p。假设在整个压缩冲程存在这些损失，且设该等效“漏气率”为η，则可将式(3)预测公式修正为

(4)

1.2.3 理论倒拖最大缸压模型

将纯压缩过程倒置，如果能获取或者估计上止点的缸内压力，并据此反推该膨胀逆过程中的压力，上止点处的误差就会减小。如此，问题就转换为该纯压缩曲线在上止点处的压力值的准确估计问题。该压力即为理论倒拖最大缸压，计算公式为

pdrag_max=εeκpBOOST

(5)

式中：pdrag_max为理论倒拖最大缸压；pBOOST为增压压力；εe为有效压缩比。

1.3 基于缸压信号的转速估计

转速信息是通过发动机ECU计数曲轴传感器信号经过处理后相邻两个方波脉的时间差来计算的。通过缸压信号可以计算出对应的曲轴相位，只需要找到两个相位参考点即可计算得到转速信息。因此本文中采用两种估计转速的方案：(1)在同一压缩冲程内，定义两个参考位置估算转速；(2)在相邻的压缩冲程内各定义一个参考位置，通过该参考位置的时间差估算转速。

2 试验设置

2.1 试验用发动机

试验用发动机为某直列4缸高压共轨柴油机；控制器为自主研发的发动机控制单元EC3200D，并通过自主研发的缸内燃烧解析单元(in-cylinder combustion analysis tool,iCAT)分析缸压数据。发动机主要参数如表1所示。

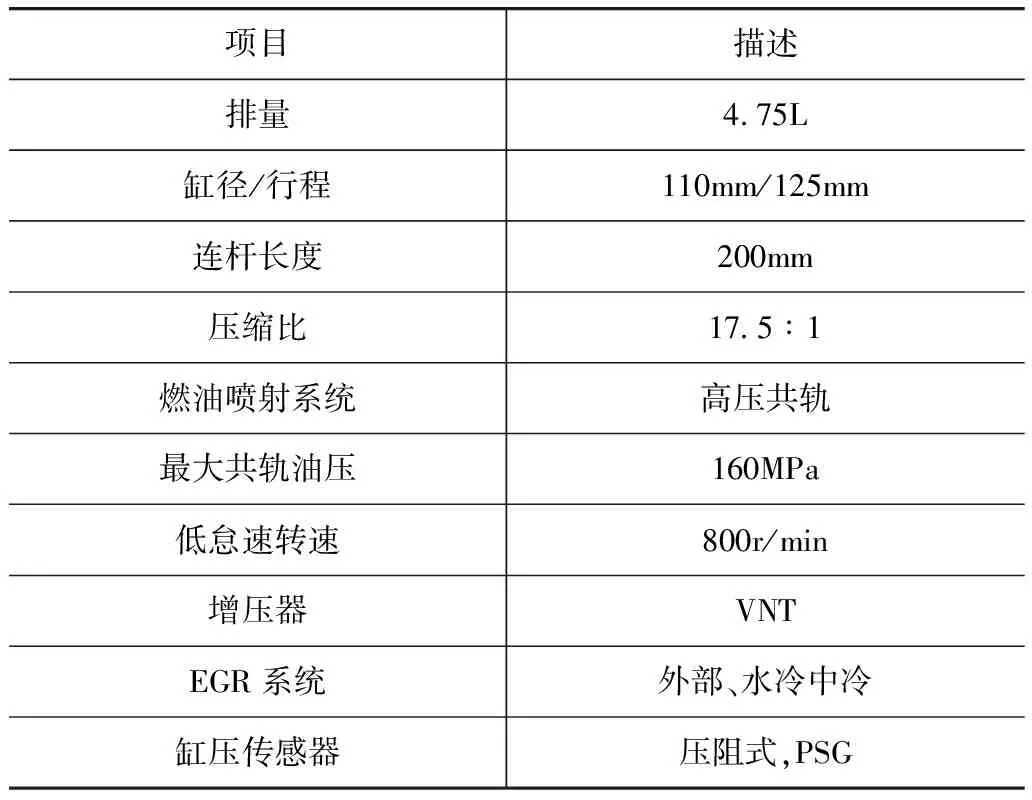
表1 发动机主要参数

2.2 缸内燃烧解析单元iCAT

缸压采集处理装置采用自主研发的新一代iCAT，其解析框图如图1所示。

iCAT负责缸压信号的采集与处理和指标的实时计算与反馈，由ECU负责发动机管理，两者之间通过CAN总线或者BDM通信方式进行数据交换。

2.3 试验设置

试验均在发动机台架测试系统上完成。试验设置如图2所示。

3 试验结果与分析

3.1 基于缸压信号的气缸识别

图3显示了在凸轮轴信号丢失时发动机某次起动中的同步过程。图中黑色脉冲为控制器中设置的标志信号，以表征控制器运行中一些特殊的状态。在连续校验几个曲轴齿形间隔之后，控制器确认已经出现曲轴信号，发动机处于起动状态；在控制器发现某齿间时间间隔为普通齿间时间间隔的3倍时(对应两个缺齿)，则认为发现缺齿，此时曲轴信号已同步。根据曲轴缺齿所处的相位位置可以知道缺齿之后第17个齿附近为第1、4气缸的上止点，此时检测发现第4缸缸内压力明显升高至2MPa左右，而第1缸缸内压力依然保持进、排气压力，因此可以判定该上止点为第4缸的压缩上止点，第1缸的进、排气上止点，此时相位完全同步，相位基准已经确立，可以准备进行燃油喷射并开始起动过程。至此，发动机已经可以完全脱离凸轮轴信号而正常运行。

3.2 基于缸压信号的曲轴相位估计

3.2.1 理想气体压缩模型

发动机倒拖至1 100r/min时采用理想气体压缩模型的预测结果如图4中虚线所示。由图可见，用该模型得到的缸压曲线预测效果并不好，实际缸压曲线始终在预测缸压曲线的下方，在上止点处预测值的缸压误差达到约16%。造成这些误差的主要原因包括：(1)用几何压缩比作为有效压缩比产生的误差；(2)忽略缸壁传热损失和活塞环漏气损失以及将绝热指数简化为定值所产生的误差。

3.2.2 简单漏气模型

同样的1 100r/min倒拖工况，使用简单漏气模型的缸压预测结果如图4中点线所示。使用简单漏气模型，压缩末期的缸压预测误差已经降低到0.12MPa之内，而且该模型对压缩起始阶段的缸压预测结果影响很小。

简单漏气模型的关键是确定等效“漏气率”，由于该等效“漏气率”与发动机倒拖工况之间难以建立物理模型，只能依靠标定的方法确定全工况的等效“漏气率”。另一方面，在简单漏气模型里，对进气压力进行一次性修正，进气时缸内压力的误差在压缩过程中会被因压缩比的存在而放大。若在进气压力的测量上有0.01MPa的误差，以压缩比为17.5计算，压缩至上止点时的预测缸压会产生约0.5MPa的误差。这对曲轴相位的估计会带来约6.6°CA的误差。因此，简单漏气模型虽然有效，但并不实用。

3.2.3 理论倒拖最大缸压模型标定

为了建立假想最大倒拖缸压随发动机转速与增压压力而变化的模型，首先进行发动机稳态工况点试验。试验点选取覆盖发动机的转速范围800～2 400r/min，间隔为100r/min，共选取58个稳态工况点。假想最大倒施缸压等高线图如图5所示。由图可见，理论倒拖最大缸压随转速变化十分平缓，而与增压压力有直接的关系。因此理论倒拖最大缸压与增压压力之间的关系变成如下简单的线性关系：

pdragmax=εeκpBOOST=kpBOOST

(8)

对试验数据进行拟合，可以得到最大倒拖缸压与增压压力的关系为

pdrag_max=0.04087pBOOST+0.28136

(9)

式中：pdrag_max以MPa为单位；pBOOST以kPa为单位。拟合结果如图6所示。对比式(8)，该拟合直线并不通过零点，除了误差的影响之外，各种简化所包含的非线性环节也是重要原因。其线性相关系数也说明该最大倒拖缸压只与进气压力相关。

3.2.4 理论倒拖最大缸压模型验证

为了验证基于缸压信号的曲轴相位估计的效果，选取了与标定试验点不同的工况进行试验，结果见图7～图11。由图可见，对于所选验证工况点，在曲轴相位估计范围内，相位估计的误差都在3°CA之内；在主喷开始前10°CA范围内，相位估计的误差都在1°CA之内。这样的相位估计精度不仅足以满足曲轴信号失效时“跛行回家”的需要，同时也为建立基于缸压的燃油喷射控制体系的提供了良好的基础。

3.3 基于缸压信号的转速估计

如原理分析部分所述，转速的估计是在相位估计的基础上进行的，选取的试验点与相位估计选取的试验点相同。方案1，同一压缩冲程内选取的两个参考相位点是(-30°CA，-10°CA)；方案2，相邻缸间的参考相位点是-15°CA。结果如表2所示。

由表2可见，方案1的计算误差波动较大，绝对误差范围为2～56r/min，对应的相对误差为0.1%～4.7%；方案2的绝对误差和相对误差都很小，分别为2～6r/min和0.2%～0.6%。二者的绝对误差相差较大，采用方案2进行转速估计的精度很高，这是由高精度的相位估计保证的；此外从理论上说，较长时间间隔的计算也可减小误差。然而，不可否认的是，试验是在稳态条件下进行的，对于瞬态变化时两个方案的精度问题还有待研究，尤其是对于方案2，其计算结果更接近于平均转速的概念。总之，两种方案的转速估计都满足精度要求，可以配合使用相互校验，甚至设计数字处理递推算法来得到更加精确和稳定的结果；但相对而言，方案2的转速估计精度较高，一般情况下，宜优先考虑。

4 结论

本文中从基于缸压信号的气缸识别、曲轴相位估计和转速估计3个方面探索了用缸压信号替代凸轮轴信号和曲轴信号的可能性，得出的结论如下。

(1) 基于缸压信号的发动机判缸:本研究中实现了发动机的无凸轮轴信号起动试验，证明发动机缸压传感器可以完全取代凸轮轴传感器。

(2) 基于缸压信号的曲轴相位估计:本文中从理想气体压缩模型出发，提出了实用的理论倒拖最大缸压模型，定义了理论倒拖最大缸压这一参量，发现该参量与增压压力之间有较好的线性关系。验证了该模型在燃烧放热之前的缸压明显上升阶段的精度为3°CA，在上止点前10°CA范围内的精度为1°CA。因此，基于缸压信号的曲轴相位估计作为曲轴信号的后备信息，可以在曲轴信号失效时为“跛行回家”提供相位基准。

(3) 基于缸压信号的曲轴转速估计：对两种转速估计方案的精度进行了分析。结合判缸和相位估计方法，为建立基于缸压的发动机控制体系奠定了基础。

[1] 陈林.混合动力柴油发动机HCCI-CI燃烧控制系统研究[D].北京:清华大学,2009.

[2] 杨雨平.柴油机基于缸压的燃烧闭环控制技术研究[D].北京:清华大学,2010.

[3] 周能辉,谢辉,赵华,等.汽油HCCI发动机实时控制系统的开发[J].中国机械工程,2009(8):970-974.

[4] 杨福源,杨雨平,欧阳明高,等.柴油机基于缸压的闭环反馈控制技术[J].内燃机学报,2012,30(2):172-178.

[5] Schiefer D,Maennel R,Nardoni W.Advantages of Diesel Engine Control Using In-Cylinder Pressure Information for Closed-Loop Control[C].SAE Paper 2003-01-0364.

[6] Liebig D,Krane W,Ziman P,et al.The Response of a Closed Loop Controlled Diesel Engine on Fuel Variation[C].SAE Paper 2008-01-2471.

[7] Beru A G.Pressure Sensor Glow Plug(PSG)[EB/OL].[2009-09-03].http://www.beru.com/english/produkte/psg.php.

[8] Yoon M,Lee K,Sunwoo M,et al.Cylinder Pressure-Based Combustion Phasing Control of a CRDI Diesel Engine[C].SAE Paper 2007-01-0772.

[9] Schten K,Ripley G,Punater A,et al.Design of an Automotive Grade Controller for In-Cylinder Pressure Based Engine Control Development[C].SAE Paper 2007-01-0774.

[10] Gangopadhyay A,Frederick M,Paul B,et al.Control of Diesel HCCI Modes Using Pressurebased Controls[C].Proceedings of FISITA 2006 World Automotive Congress,Yokohama,Japan: JSAE,2006.

[11] Yang Fuyuan,Gao Guojing,Ouyang Minggao,et al.Research on a HCCI Engine Assisted by an ISG Motor[J].Applied Energy,2013,101:718-729.

[12] Kolbeck A F.Closed Loop Combustion Control-Enabler of Future Refined Engine Performance Regarding Power,Emissions & NVH Under Stringent Governmental Regulations[C].SAE Paper 2011-24-0171.

[13] Quillen K P,Viele M,Ciatti S A.Next-Cycle and Same-Cycle Cylinder Pressure Based Control of Internal Combustion Engines[C].Proceedings of the ASME 2010 Internal Combustion Engine Devision Fall Technical Conference,San Antonio,USA,September,2010.

[14] Seongeun Y,Han H S,Kyoungdong M,et al.Development of Engine Control Using the In-Cylinder Pressure Signal in a High Speed Direct Injection Diesel Engine[C].SAE Paper 2011-01-1418.

[15] 黄颖.面向柴油机燃烧闭环控制的新一代控制平台研究及应用[D].北京:清华大学,2011.

[16] 张科勋,周明,李建秋,等.曲轴、凸轮轴传感器故障时的电控柴油机喷射控制[J].汽车工程,2007,29(1):54-58.

[17] Brunt M,Rai H,Emtage A L.The Calculation of Heat Release Energy from Engine Cylinder Pressure Data[C].SAE Paper 981052.

[18] Brunt M F J,Platts K C.Calculation of Heat Release in Direct Injection Diesel Engines[C].SAE Paper 1999-01-0187.

[19] Grau J H.Modelling Methodology of a Spark-Ignition Engine and Experimental Validation-Part I: Single-Zone Combustion Model[C].SAE Paper 2002-01-2193.