车辆临界稳定情况下相关状态变量变化对稳定性判定准则的影响*

石 文，余卓平，熊 璐

(1.同济大学汽车学院，上海 201804；2.同济大学新能源汽车工程中心，上海 201804；3.钢铁研究总院，北京 100081)

前言

1 车辆动力学模型的建立

1.1 3自由度车辆动力学模型

首先建立单轨车辆模型动力学方程组，并假定3自由度非线性微分方程组[3]代表了本文中研究车辆的实际动力学关系：

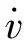
(1)

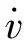
(2)

(3)

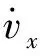
(4)

(5)

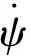
车辆纵向加速度和质心加速度之间的关系为

(6)

线性轮胎模型为

FyV=CaVαV

(7)

FyH=CaHαH

(8)

非线性轮胎模型采用魔术公式简化形式[7,10]：

(9)

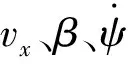
(10)

(11)

(12)

式(11)和式(12)表征了稳定性控制所跟踪的车辆侧向动力学关系。在非匀速工况下，须联立式(10)考虑车速变化对式(11)和式(12)解的影响。

车辆的运动学关系为

(13)

(14)

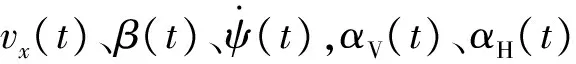
1.2 车辆瞬态稳定性分析模型

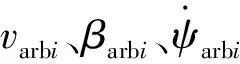
(15)

其中：

(16)

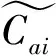
(17)

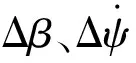
(18)

其中：

(19)

线性化之后微分方程组的齐次通解可用以下结构表示：

(20)

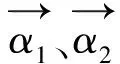
(21)

其中车辆瞬态转向特性为

(22)

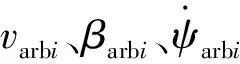
2 稳定性判定准则的常用方法

2.1 跟踪相平面稳定区域方法

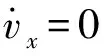
(23)

(24)

通常在使用相平面法作为稳定性判据时，须对车辆在各个匀速工况下的受力和各项可变参数进行准确分析，得到与该工况对应的常微分系统方程。之后将各个常微分方程组所对应相图的稳定区域特征信息进行综合，建立查表数据库，供稳定性控制系统调用[7,13]。从理论上讲，相平面法是一种定性判断车辆侧向动力学特性的方法，但该控制方法要求查表数据库可以完整覆盖车辆可能出现的各个匀速工况，且要求选用的理论模型具有足够高的精度以准确反映对应工况下车辆的动力学特性。由此可知，基于相平面稳定区域的判定准则需要大量数据库作为支撑，其判断的准确度与轮胎模型精度和数据量成正比。但是，车辆实际转向过程中并不总能保证匀速行驶，某些情况，由于车轮切向力的变化，使得车辆出现纵向加速度或者减速度，并且耦合前后车轴载荷变换进而改变了前后车轴的侧偏特性。瞬态下，可能使得由式(23)和式(24)得到的相图发生本质变化。由于纵向加速度会随时间对车速产生影响，相平面轨线已不能准确反映相关状态变量的变化趋势，须借助相空间分析方法。因此，这类基于匀速假设的相平面稳定区域判据存在纵向动力学影响情况下的适用性问题，还须进一步研究[14]。

2.2 跟踪线性参考模型方法

线性参考模型方法是一个相对简单、实用且有效的方法。目前产品化的稳定性控制系统大多以此方法作为稳定性控制的触发判据。其理论依据[3-4,8]为

(25)

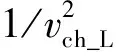
(26)

有一些厂商如MANDO[5]，通过前期试验建立查表数据库，用于限制不同路面摩擦因数情况下的理论横摆角速度最大值。以上理论模型也可用前轮转向角δV表示,须注意，此处并不考虑转向系刚度对前轴侧偏特性的影响：

(27)

在此主要关心由式(27)计算的横摆角速度理论值所对应的数学意义，及其与车辆侧向动力学非线性微分方程组中心平衡点之间的关系。

统计表明，一般驾驶员在弯道行驶时，95%情况下所能达到的侧向加速度不会超过4m/s2，即认为在轮胎侧偏特性的线性范围[1]，如图1所示。

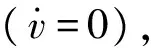
(28)

(29)

通过对式(28)和式(29)中参数的标定，可以使参考模型具有与所控车辆在轮胎侧偏特性线性范围内基本一致的不足转向性能。工业化应用时，厂家还会通过微调稳定性控制器敏感度等方法，增加参考模型对于参数变化影响的鲁棒性，使稳定性控制系统适应于各种驾驶条件。并且针对多种多样的道路条件和车辆条件(主要是载荷和轮胎变化对跟踪模型精确性的影响)制定了上百种鲁棒性测试[5]。

由于实际车辆的侧向动力学关系具有高度的非线性因素，车辆弯道行驶过程中轮胎力的变化，可能会瞬时改变前后车轴侧偏关系，从而改变中心平衡点在相平面上的位置和性质，有可能使式(11)和式(12)微分方程组的特性发生质的变化。由于式(11)和式(12)车辆侧向动力学非线性微分方程组具有参数依赖方程组的典型特点，因此，行驶工况变化所引起的轮胎切向力、车轴载荷、行驶车速和前轮转向角等参数切换均会改变车辆瞬态下常微分方程组的解析表达式。本文中研究的内容侧重于车辆瞬态情况下相平面全局特性的改变，分析式(11)和式(12)方程组中对应的可变参数不难看出：由于车速是加速度的数值积分，车轮转角的变化受到驾驶员操纵转向盘频率的影响，受到人体工程学极限的约束。所以，能够在瞬态下改变微分方程组稳定性质的因素主要是轮胎力变化，即纵向加速度引起的载荷变化和轮胎所受切向力的变化等因素对前后车轴侧偏特性的综合影响。这种前、后车轴之间具体侧偏关系的变化，既决定了车辆侧向动力学系统稳定性变化的程度，也决定了不稳定中心平衡点与之前相平面稳定中心平衡点的偏离程度。可通过特定工况说明这种由于非线性微分方程组特性瞬态变化对线性判据有效性产生的影响。

3 载荷变化工况下的车辆瞬态稳定性对现有判据有效性的影响

仿真工况取自弯道行驶车辆加速踏板松开所产生的载荷变化。选取思路是考虑到此工况出现的约-1m/s2减速度使得前轴加载、后轴减载，对于不同驱动方式车辆，该工况均拉近了前后车轴等效侧偏关系，大多数车辆不足转向程度降低甚至出现过多转向以至于失去稳定性。需要说明的是：由于减速度是由驱动轮制动力矩产生的切向反力(不考虑滚动阻力)与各种等效车身阻力(如空气阻力和曲线行驶阻力)的合力产生，大多数情况下，驱动轮总的切向反力不会大于500N，因此，在干燥路面条件下，不同驱动方式的影响均小于车轴载荷变化对车轴侧偏特性的影响[3]。车辆参数如表1所示。

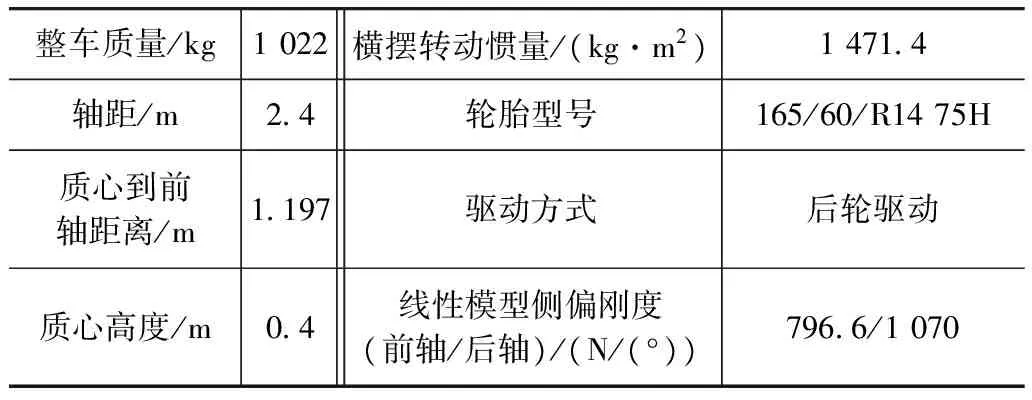
表1 车辆参数

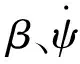
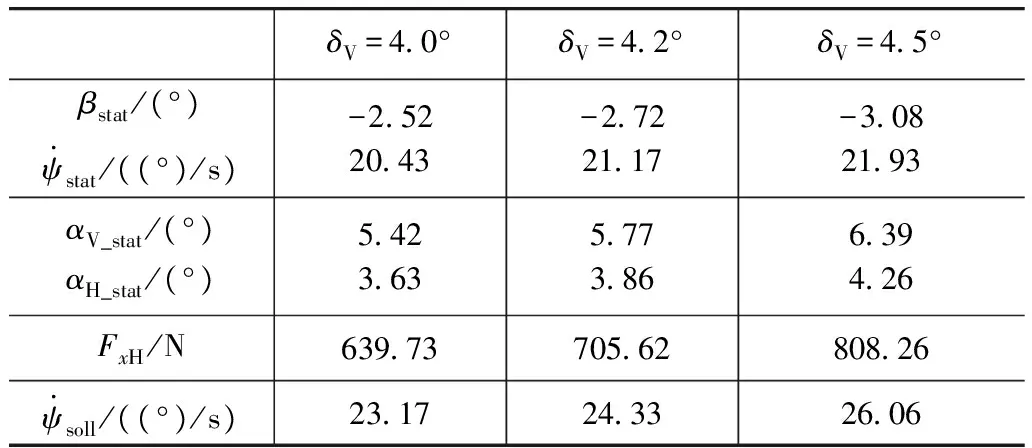
表2 车辆匀速圆周行驶时的数值计算结果

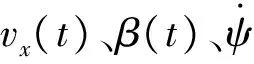
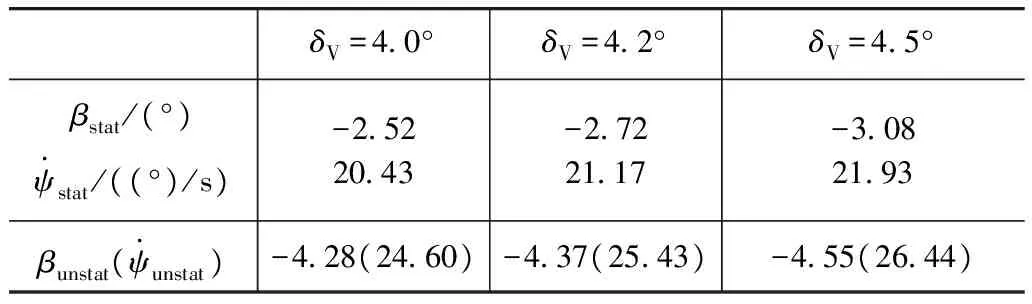
表3 载荷变化前后中心平衡点位置的变化

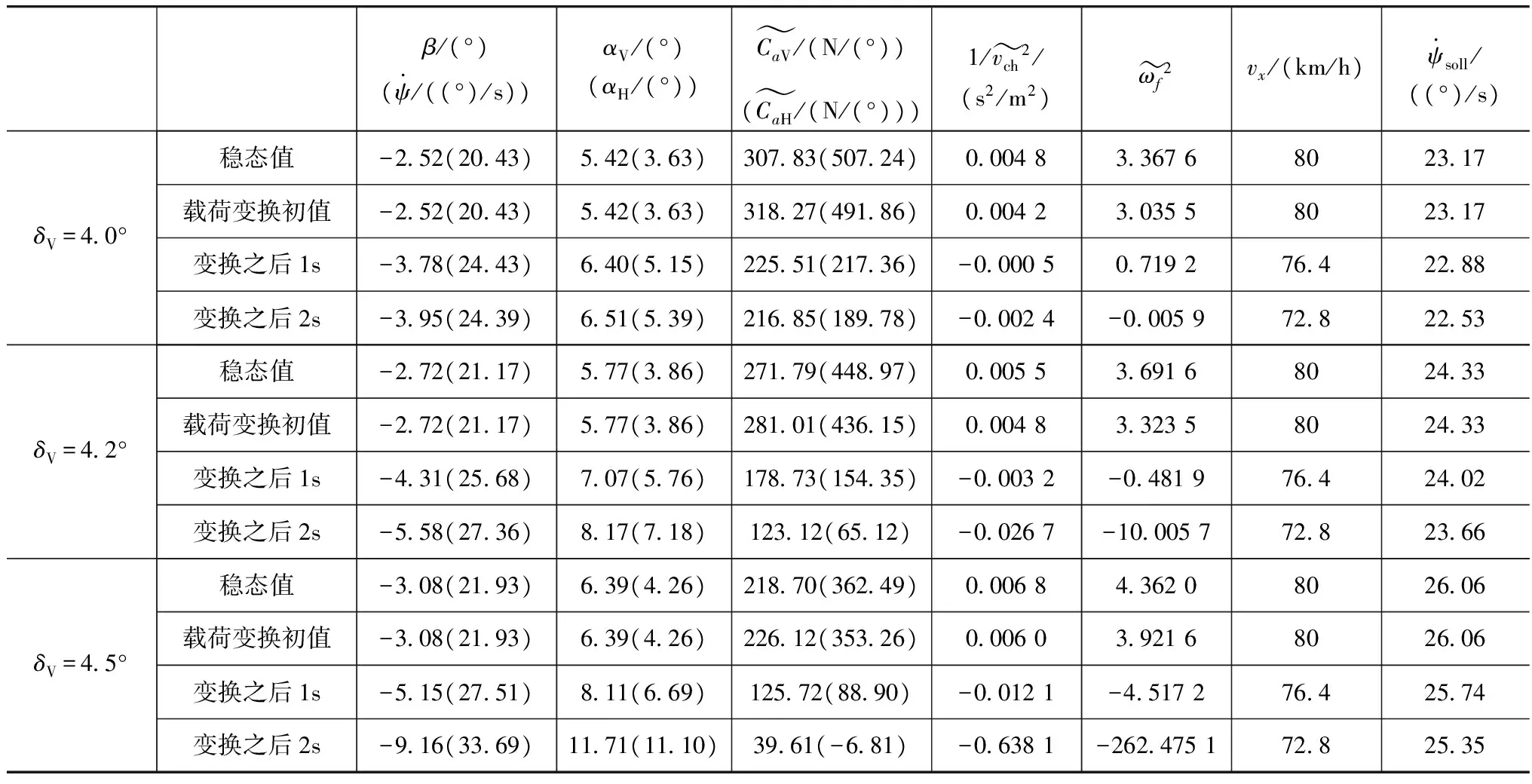
表4 3种前轮转角情况下车辆瞬态稳定性的变化过程

特定工况下，虽然车辆侧向动力学非线性微分方程组特性发生质的变化，即式(11)和式(12) 2自由度系统的中心平衡点特性由之前的稳定焦点变为鞍点，但是其位置并没有发生很大变化。由式(27)得到的横摆角速度理论值与非线性系统中心平衡点所对应的非稳定稳态横摆角速度值接近。虽然稳定性判据可能认为此时车辆是稳定的，但实际车辆的侧向动力学特性不稳定。由于线性参考模型方法不是跟踪车辆系统自身稳定性变化，因此，研究这一类工况中式(10)～式(12) 3自由度非线性微分方程组的特解在非稳定中心平衡点连续统邻域内的变化规律，对于了解参考模型方法在该类工况下的有效性就具有积极的意义。

4 结论

相平面法可以定性研究车辆侧向动力学系统特性和特解轨线的变化过程。在相平面法用于稳定性判据时要求理论模型的精确性，且需要前期对各种匀速工况细分以建立尽可能完备的查表数据库。不同于非线性系统方程数学意义上的稳定性，车辆瞬态稳定性变化需要一个过程。对于车辆实时稳定性控制所跟踪的最重要状态变量横摆角速度和质心侧偏角的数值增量，更是描述车辆瞬态稳定性所对应线性化微分方程组数值积分的结果，这两个变量增量的变化具有明显的连续性。因此，定性分析车辆侧向动力学微分方程组解的稳定区域作为控制判据和控制决策的方法不如跟踪线性参考模型方法效率高。在某些考虑纵向动力学影响的临界稳定情况下，由于车辆稳定性控制所跟踪的状态变量会在不稳定中心平衡点连续统邻域内一段时间变化缓慢，且数值接近于线性参考模型理论值，可能使得稳定性控制系统不能及时响应而错过最佳时机。因此，须针对此类工况特点，对线性参考模型参数或者误差门限值进行调整，从而达到更好的控制效果。

[1] Inagaki Shoji,Kshiro Ikuo,Yamamoto Masaki.Analysis on Vehicle Stability in Critical Cornering Using Phase-Plane Method[C].AVEC’94,No.9438411:287-292.

[2] Ko Young Eun,Lee Jang Moo.Estimation of the Stability Region of a Vehicle in Plane Motion Using a Topological Approach[J].International Journal of Vehicle Design,2002,30(3):181-192.

[3] 米奇克,瓦伦托维茨.汽车动力学[M].陈荫三,余强,译.北京:清华大学出版社,2009.

[4] Van Zanten Anton T,Robert Bosch GmbH.Evolution of Electronic Control Systems for Improving the Vehicle Dynamic Behavior[C].AVEC’02,No.20024481.

[5] Kim Dongshin,Kim Kwangil,Lee Woogab,et al.Development of Mando ESP (Electronic Stability Program) [C].SAE Paper 2003-01-0101.

[6] 哈里尔.非线性系统[M].朱义胜,等译.北京:电子工业出版社,2011.

[7] Von Vietinghoff A.Nichtlineare Regelung von Kraftfahrzeugen in Querdynamisch Kritischen Fahrsituationen[D].Universität Karlsruhe,2008.

[8] Rajesh Rajamani.Vehicle Dynamics and Control[M].New York,Dordrecht,Heidelberg,London: Springer,2012.

[9] 王德平,郭孔辉,宗长富.车辆动力学稳定性控制的理论研究[J].汽车工程,2000,22(1):7-9.

[10] Von Vietinghoff A,Lu H,Kiencke U.Detection of Critical Driving Situations Using Phase Plane Method for Vehicle Lateral Dynamics Control by Rear Wheel Steering[C].The International Federation of Automatic Control,2008:5694-5699.

[11] True H.On the Theory of Nonlinear Dynamics and its Applications in Vehicle Systems Dynamics[J].Vehicle System Dynamics,1999,31(5-6):393-421.

[12] Crolla D,喻凡.车辆动力学及其控制[M].北京:人民交通出版社,2003.

[13] 邓律华.极限工况下车辆行驶的稳定性判据[D].上海:同济大学,2013.

[14] Tchamna R,Youn I.Yaw Rate and Side-slip Control Considering Vehicle Longitudinal Dynamics[J].International Journal of Automotive Technology,2013,14(1):53-60.