对一道课本习题的思索

俞相顺

(南京市溧水区石湫中学，江苏南京，211222)

一、例题

在九年级数学的教学中有这样一道题：如图1，在直角梯形ABCD中，∠B=∠C=90°，E是BC的中点，DE平分∠ADC，求证：AE平分∠BAD。此题可以用多种方法证明。

图1

(一)证法一，如图1

作EF⊥AD，垂足为F

∵EC⊥CD，EF⊥AD

DE平分∠ADC

∴EC=EF

又∵E是BC的中点，EB=EC

∴EB=EF，且EF⊥AD，EB⊥AB

∴ 点E在∠BAD的平分线上

即AE平分∠BAD

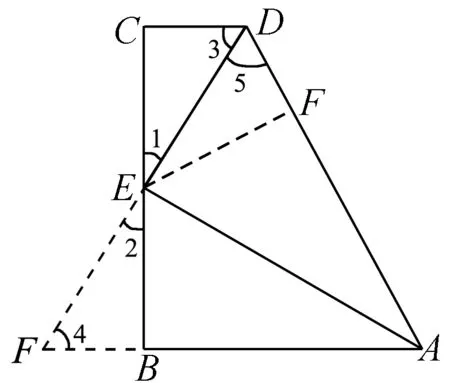
图2

(二)证法二，如图2

延长DE与AB的延长线交于点F

∵EC=EB， ∠C=∠EBF=90°， ∠1=∠2

∴ △ECD≌△EBF

∴ED=EF， ∠3=∠4

又∵ ∠3=∠5

∴ ∠4=∠5

∴ △ADF为等腰三角形，且AE是底边上的中线

∴AE平分∠BAD

图3

(3)证法三，如图3

作EF∥AB

∵E是BC中点

∴F是AD中点

∵ ∠1=∠2，∠1=∠3

∴ ∠2=∠3

∴DF=EF=AF

∴ ∠4=∠5

又∵ ∠4=∠6

∴ ∠5=∠6，即AE平分∠BAD

二、条件与结论的变式

初做此题，并未多想，只是觉得它是一道很普通的一题多解题。但在以后的教学中发现这个基本图形经常出现，这引起了笔者进一步思考。

(一)结论变式

不难发现此题还有AE⊥DE，AD=AB+CD这两个结论。在解完此题后对这两个结论的证明应该很容易了。

(二)条件变式

如果把题中的直角梯形换成一般梯形，问题还能解决吗？上面的两个结论还能成立吗？仔细思考，会发现两个结论仍然成立，只不过证明时，不能用证法一来证明。

(三)条件和结论互换变式

又经过一番思考，笔者有了一个猜想，对于此题中的五个条件(或结论)，即EC=EB，DE平分∠ADC，AE平分∠BAD，AE⊥DE，AD=AB+CD，只要知道了其中两个就可以用来证明其他三个，于是又有了以下变式。

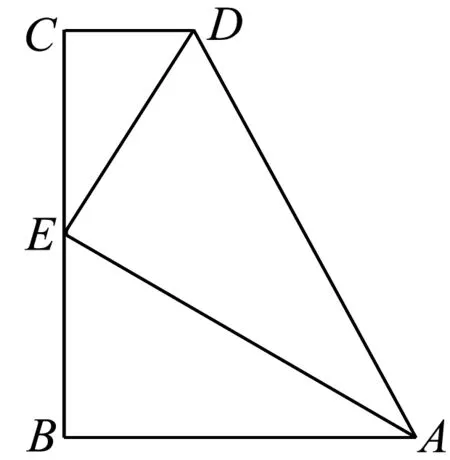
图4

变式一：如图4，在梯形ABCD中，AB∥CD，E是BC上一点，且DE、AF分别平分∠BAD、∠CDA。求证：①AE⊥DE；②E是BC中点；③AD=AB+CD。

变式二：如图4，在梯形ABCD中，AB∥CD，E是BC上中点，且AE⊥DE。求证：①DE、AF分别平分∠BAD、∠CDA；②AD=AB+CD。

变式三：如图4，在梯形ABCD中，AB∥CD，E是BC上中点，AD=AB+CD。求证：①AE⊥DE；②DE、AF分别平分∠BAD、∠CDA。

变式四：如图4，在梯形ABCD中，AB∥CD，AD=AB+CD，且DE平分∠CDA。求证：①AE⊥DE；②AF平分∠BAD；③E是BC中点。

变式五：如图4，在梯形ABCD中，E是BC上的一点，AD=AB+CD，且AE⊥DE。求证：①E是BC中点；②DE、AF分别平分∠BAD、∠CDA。

对以上变式，经过论证，意外地发现前四个变式都可以证明出来，而只有变式五无法证明。所用的证明方法就是前面证法的一些逆向思维。

三、进一步思考

从这道题的一系列变式中可以发现我们运用了许多知识，同时也可以归纳出一些方法，找到题目中一些规律性的结论，可是仍有一个变式不能证明。再回到原题，笔者又想到了这样一个问题，即在满足条件“一腰等于两底和”的梯形中，另一腰的中点与前腰两端点的连线互相垂直且分别平分两个底角，在这样的梯形中，这几个关系应达到一种和谐的统一。但为什么变式五无法证明呢？把原来直角梯形这一条件加上去呢？

已知：如图5，在直角梯形ABCD中，∠B=∠C=90°，E是BC上一点，AD=AB+CD，且DE⊥AE，求证：E是BC中点，DE平分∠CDA。

分析：此题用“同一法”可以证明。

取AD中点F，过F作FG⊥CB，垂足为G，连接EF

∴GF=1/2(AB+CD)=1/2AD

图5

又∵EF=1/2AD

∴EF=FG，而FG⊥CD

∴FE与FG重合

∴FE∥CD

∴E是BC中点，易证DE平分∠CDA

由此可见，在一腰等于两底和的直角梯形中，一定能在另一腰上找到一点，使得该点与前腰两端点连线互相垂直，且这一点必定是该腰的中点，也就是说这样的点有且只有一个。

用上面的分析去思考前面无法证明的变式五，变式五中的图形其实就相当于将图6中的BC绕点E旋转一定角度得到，如图9，显然，此时⊙F与B1C1有两个交点，也就是说B1C1上满足条件ED⊥AE的点E不止一个，这就很好地解释了为什么变式五无法证明。

图6

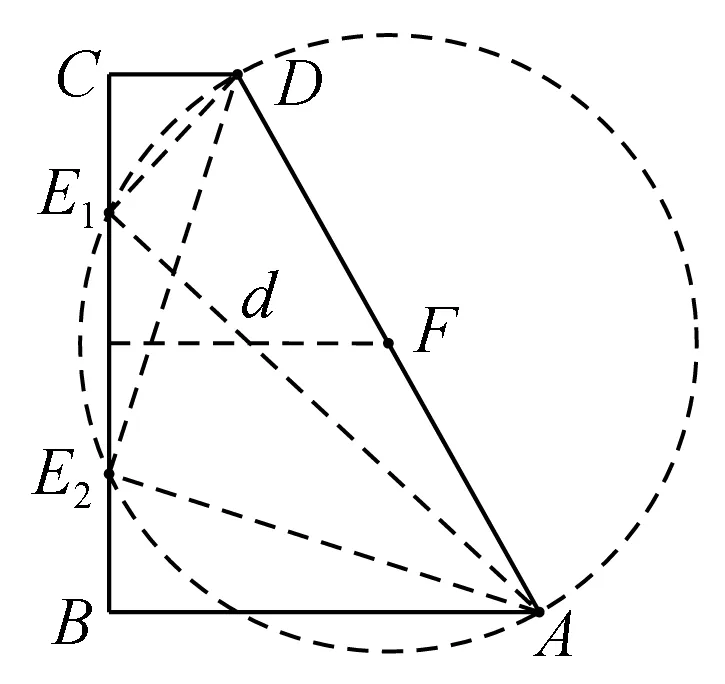
图7

图8

图9

[1] 李德忠，董方英.圆与梯形相珠联——对一道课本习题的探究[J].中学数学，2010(7).

[2] 方先进，张连姣.习题·模式·应用[J].中学生数学，2005(3).

[3] 端凡侠.从《梯形》中一道习题得出的重要结论[J].初中生世界，2004(1).