如何寻求计算教学中的“理法”交融

浦冬梅

(南通市如东县大豫镇兵房小学，江苏南通，226412)

一、厘清算理和算法的关系

算理为运算过程中的道理，是用来证明计算过程中的理由和正确性，说明“为何要这么算”的。算法则是阐述在计算过程中所要遵循的规则和计算顺序，它往往是依据算理人为制定的一些规则。

以两位数加两位数笔算(进位)运算法则为例，“个位与个位对齐，十位和十位对齐，从个位加起。个位相加满10，要向十位进1”，这个运算法则非常清晰地规定了计算时的方法和先后顺序。 规定“个位和个位对齐，十位和十位对齐”，是因为不同位置上的数字计数单位不同，只有相同单位的数字才可以相加。而“个位相加满10，要向十位进1”则是依据“十进位值制”所规定的规则。事实上，对于两位数不进位加法，从十位加起完全可以，但是对于两位数进位加法，如果从十位加起，则个位上若满了10 还需到十位上再加1。这样计算就变得麻烦，容易出现错误。为了减少学生的错误，让计算变得简便才规定了“从个位加起”。由此可见，两位数加法的算理是“十进位值制”和“相同单位的数才能相加”，“从个位加起”则是为了计算的简便和减少错误人为规定的。由此可以看出，算理和算法相辅相依，不可缺一。

二、借助直观教学，感悟算理，提炼算法

(一)利用学具，在操作中明理懂法

苏教版三年级《除法》教学片段：师出示例题图，提出问题：“把72个乒乓球平均分给2个班，每个班能分到多少个？”

师：谁能来说说你的想法？你是怎么分的？

生1：我是先把这7捆小棒全部散开，把这2根和它们合起来，再把这72根小棒平均分成两份，就知道了每份是36根。

生2：我是先把这6捆小棒平均分成了2份，每份有3捆；接着把这2根也平均分成2份，每份1根；那剩下的1捆小棒一共有10根，把它们都散开来，平均分成2份，每份就是5根；最后就把所有的小棒都平均分成了两份，每份小棒是36根。

生3：我先把7捆中的6捆拿出来平均分成2份，每份有2捆；还剩下1捆没办法直接分，我就把这1捆小棒全部散开，和2根合起来，一共是12根，把这12根小棒再平均分成2份，每份6根；最后合起来得到每份36根。

师：以上三种分法，你们觉得哪种比较好？为什么？

生4：第一种分法太麻烦，第二种和第三种差不多。

师：第二和第三种分法有什么相同的地方？

生5：它们都是先拿出6捆平均分成两份，然后再把最后一捆拆开来继续分。

师：哪一种分法更为简洁合理？

生5：第二种要分三次，第三种只要分两次，第三种分法比较简便。

师：大家能把这种分法再说一说吗？

(生复述)

师：你们能一边想刚才分小棒的过程，一边把竖式写完整吗？(板书学生的竖式)你在计算时先除哪一位上的数字？这个十位上余下来的1表示的是什么意思？接着往下又该怎么除呢？

心理学家皮亚杰曾经说过：“智慧的鲜花是开放在指尖上的。”动手操作实践能把抽象的数学知识变得简单而具体，符合小学生直观形象的思维特征。因此，借助于直观操作、动手实践来帮助学生的思维理解是非常必要的。在上面的教学过程中，教师通过一捆完整的小棒不能平均分给两个班的思维冲突，使学生自觉地感悟到要把它拆分成10根并与另外两根合起来再继续分。这一过程其实解释了竖式中十位上余下来的1是表示什么意思，加上教师对第二、三种分法的对比，使学生意识到在竖式计算中要先算十位，再把余下的数合起来算的合理性。

(二)数形结合，感悟算理，提炼算法

苏教版六上《分数乘分数》教学片段：

(教师在教学完例4之后，提出问题)

师：你们觉得分数乘分数应该怎样计算？

生1：分数与分数相乘，用分子和分子相乘的积作为分子，分母和分母相乘的积作为分母。

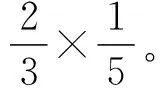
(有了例题4的经验，学生很自然地想到了画图的方法……)

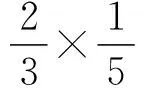
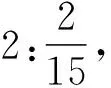
(学生们陷入沉默)

(生带着思考自主画图)

师：说说你是怎样来画图的？

师：讲得真清楚！想一想你们的画图过程，分母乘分母，实际上表示的是什么意思？分子乘分子又是表示什么意思呢？

生3：分母相乘求的就是把单位“1”分了两次，一共分成了多少份，分子相乘就是求取了两次一共取了多少份。

从上面的案例可以看出，学生计算“分数乘分数”的过程是以对“分数意义”的理解作支撑，这个过程对于帮助学生形成系统的数学知识结构非常重要。在教师抛出“为什么这样做就是正确的呢”问题后，学生借助图形，分析时有理有据，数形结合的方式很好地帮助学生建立起立体生动的数学思维。这样的教学过程不仅传授了知识和技能，更培养了学生的数学思维能力。

[1] 郭长春.简议计算教学中动手操作的有效性——从三年级“笔算除法”说起[J].课程教材教学研究：小教研究版，2012(9).

[2] 费岭峰，胡慧良.在意义理解中实现探究的价值——对“分数乘分数”算法探究的思考[J].教学月刊：小学版(数学)，2011(8).