一类Lotka-Volterra合作系统的四个正周期解问题
张友梅
(合肥职业技术学院基础部,安徽 巢湖 238000)
1 引言
近年来,各类生物模型的周期解的存在性得到广泛的研究。考虑到时滞的影响,考虑以下带收获项的时滞Lotka-Volterra合作系统:
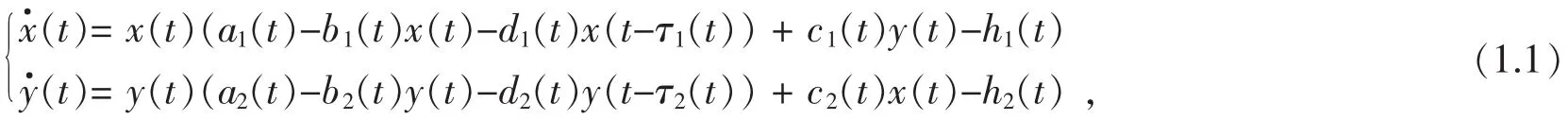
其中 x(t)和 y(t)分别表示合作种群的密度;ai(t),bi(t),di(t),τi(t),ci(t),hi(t),h=1,2 都是正的连续函数,分别表示自然增长率,成虫死亡率,幼虫死亡率,时滞,合作效率和两种群的收获率。对于该种群模型的详细介绍,可参看文献[1-5]。
重合度理论是研究周期解的存在性和多解性的重要工具[6-7]。受以上论文的启发,我们利用重合度理论来研究模型(1.1)多个正周期解的存在性。 此外,假设(1.1)中所有的参数都是正的ω-周期函数,ω>0.
2 预备知识
首先介绍几个相关概念。
令X,Z是赋范向量空间,L:D omL⊂X→Z是线性映射,N:X×[0,1]→Z是连续映射。如果dim KerL=codim ImL<∞且I mL在Z中是闭的,则称L为Fredhol映射。如果L是指标为0的Fredhol映射,则存在连续映射 P:X→X 和 Q:Z→Z,使得 I m P=KerL,I m L=Ker Q=I m(I-Q),X=KerL⊕Ker P,Z=I m L⊕ I m Q.因此LDomL∩KerP:(I-P)X→I m L是可逆的。记KP为L映射的逆。如果Ω为X的有界开子集,且QN×[0,1])是有界的,Kp(I-Q)N:× [0,1]→X 是紧的,则称 N 在× [0,1]上为 L-紧的。因为 I mQ 和 KerL 是同构的,所以存在同构映射J:I mQ→KerL.
定理2.1[8]令L是指标为0的Fredholm映射,且令N在×[0,1]上是紧的,设
下面给出文中用到的一些记号:对于连续ω-周期函数f(t),记:
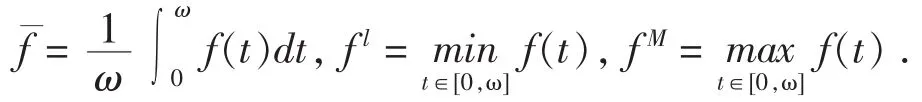
再作假设如下:
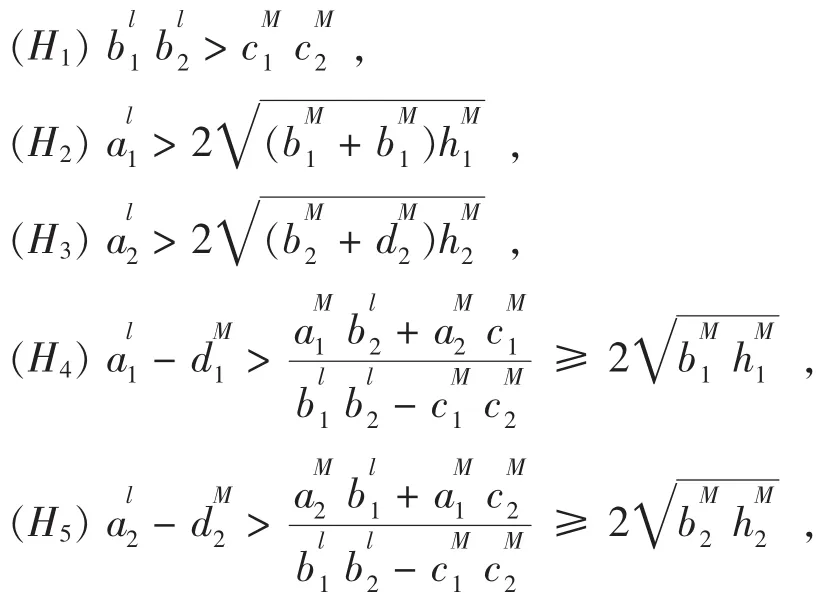
记八个正数如下:

3 四个正周期解的存在性
定理 2.2 若条件(H1),(H2),(H3),(H4),(H5)成立,则系统(1.1)至少存在四个周期解。证明:首先利用变量代换

则模型(1.1)可变为:


因为P,Q是连续的投影,所以ImP=K erL,K erQ=ImL=Im(I-Q).则L是指标为 0的Fredholm映射。 算子 L的广义逆算子则有
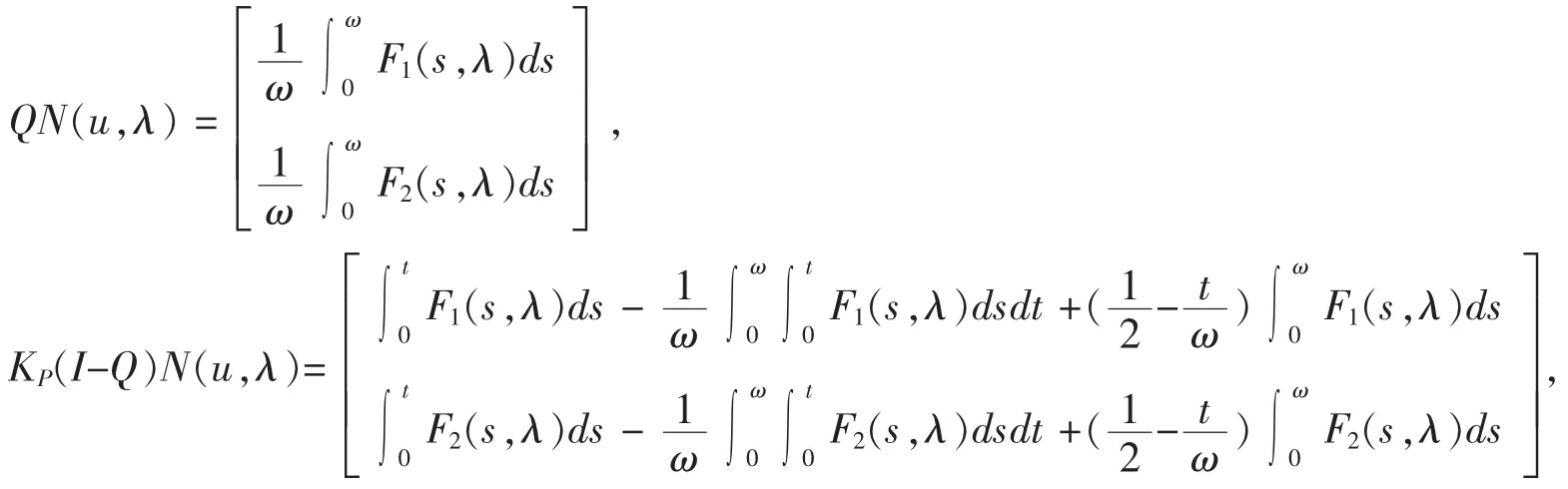
这里
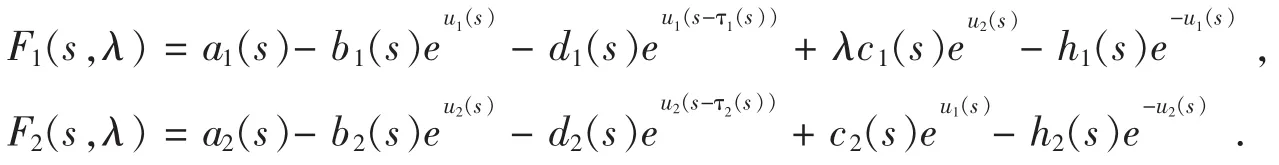
QN和KP(I-Q)是连续的。用Arzela-Ascoli定理容易验证对任意的有界开集是紧的。进一步,是有界的。因此在上,对于任意的有界开集Ω⊂X,N是L-紧的。
为了利用定理2.1,必须在X中找到至少4个合适的有界开子集。考虑算子方程L x=λN(x,λ),λ∈(0,1)得到:
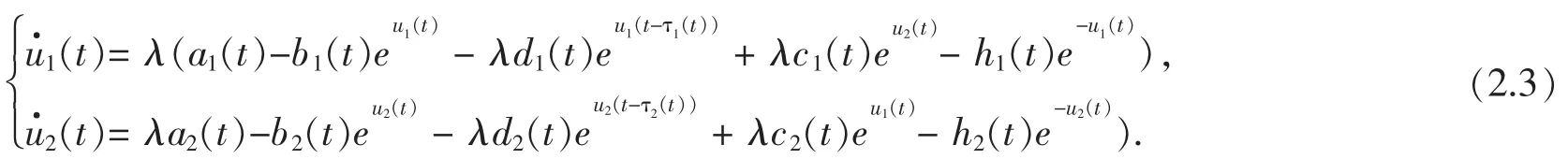
假设存在 λ∈(0,1),u∈X 是方程组(2.3)的一个 ω-周期解。 则存在使得
ui(ξi)=且有
由以上讨论和(2.3)有:

(2.4)(a)和(b)给出:
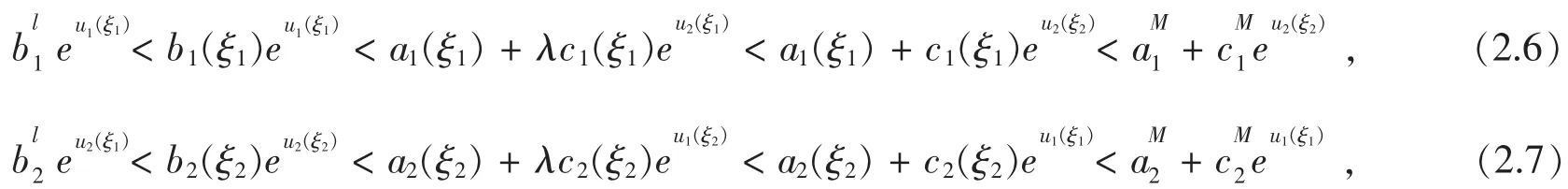
从(2.6),(2.7)有
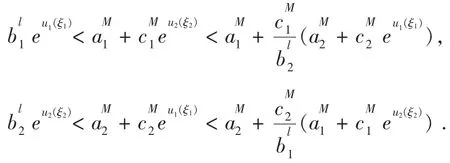
由(H1),有

即

同理由(2.5)(a)和(b)和(H1),得
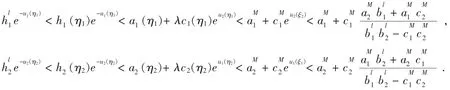
则

即

然后可得

注意到

由这个不等式和(H2),可得

那么有

类似地,由(2.4)(b)及(H3)得
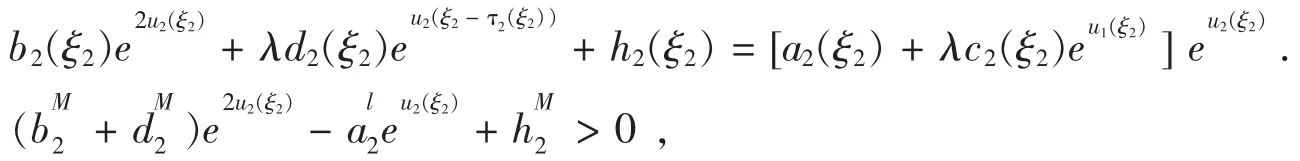
则

同理,由(H4)和(2.5)(a)可得

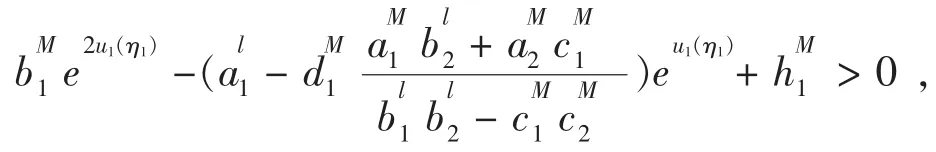
则

类似地,由(H5)和(2.5)(b)可得

从(2.8),(2.10),(2.12),(2.14)得

或者

从(2.9),(2.11),(2.13),(2.15)得

或者

显然,K1,K2,K3,K4,K5,K6,K7,K8是不依赖于 λ 的。
现作
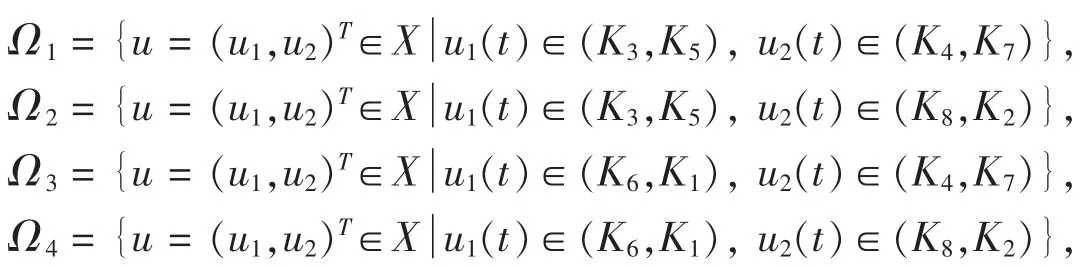
那么有 Ωi(i=1,2,3,4)是 X 的有界开子集,且 Ωi∩ Ωj= φ,i≠j,i, j=1,2,3,4.因此 Ωi(i=1,2,3,4)满足定理 2.1 的条件(1).
下面证明定理 2.1 的条件(2)也是满足的。 即要证当 u∈∂Ωi∩KerL=∂Ωi∩R2时,QN(u,0)≠(0,0)T(i=1,2,3,4).若该结论不成立,则当 u∈∂Ωi∩KerL=∂Ωi∩R2,(i=1,2,3,4),常向量 u∈∂Ωi(i=1,2,3,4)满足

因此存在两个点 ti=(i=1,2)满足

由(2.16)-(2.19),有

所以 u∈Ω1∩R2或 u∈Ω2∩R2或 u∈Ω3∩R2或 u∈Ω4∩R2,这与 u∈∂Ωi∩R2(i=1,2,3,4)是相矛盾的,这就证明了定理2.1的条件(2)是满足的。
最后证明定理 2.1 的条件(3)也满足。 由条件(H1),(H2)得方程组
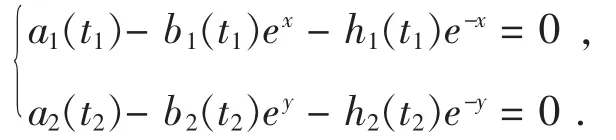
有4个不同的解,它们分别是

这里
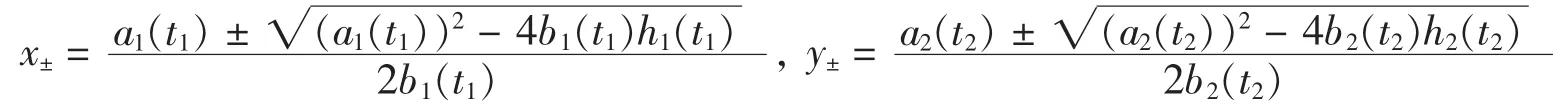
易证:
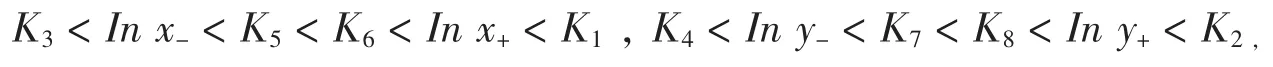
因此
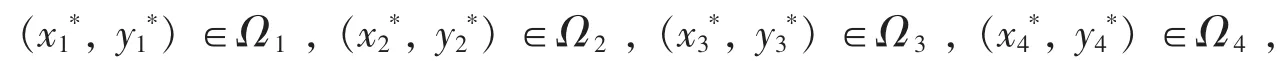
因为K erL=ImQ,J=1则:
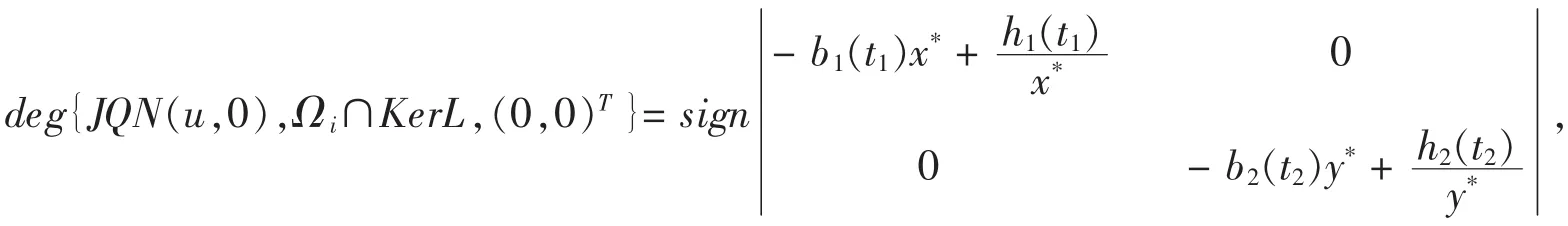
因为

故有
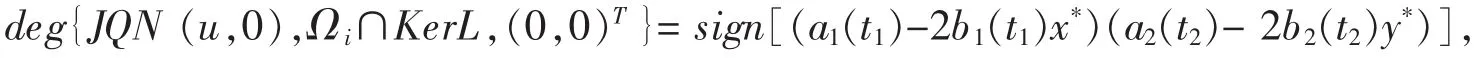
所以

至此,证明了Ωi(i=1,2,3,4)满足定理2.1中的所有假设条件。因此模型(2.2)至少存在4个不同的ω-周期解。以(1.1)至少存在4个不同的正的ω-周期解,定理2.2得证。
[1] 马知恩.种群生态学的数学建模与研究[M].合肥:安徽教育出版社,1996:46-55.
[2] Zhengqiu Zhang,Zhicheng Wang.The existence of a periodic solution for a generalized predator_prey system with delay[J].Math.Proc.Cambridge Philos.Soc.,2004,(137):475-486.
[3] Zhengqiu Zhang,Zhicheng Wang.Periodic solutions of a two-species ratio-dependent predator-prey system with time delay in a two-patch environment[J].ANZIAM J.,2003,(45):233-244.
[4] Zhengqiu Zhang,Jun Wu,Zhicheng Wang.Periodic solutions of nonautonomous stage-structured cooperative system[J].Comput.Math.Appl,2004,(47):699-706.
[5] Yongkun Li.Periodic solutions of a periodic delay predator-prey system[J].Proc.Amer.Math.Soc.1999,(127):1331-1335.
[6] 刘娟风,魏凤英.具有捕获的三种群Lotka-Volterra系统的多个周期解[J].福建师大福清分校学报,2010,(5):1-8.
[7] 雷慧榕,魏凤英.具有捕获的四种群捕食系统的多个正周期解[J].福州大学学报(自然科学版),2011,(2):167-172.
[8] R.E.Gaines,J.L.Mawhin.Coincidence degree and nonlinear differential equations,in Lecture Notes in Mathematics,vol.568[M].Berlin:Springer-Verlag,1977.

