一类行列式的解法
秦喜梅
(巢湖学院数学系,安徽 巢湖 238000)
行列式是代数学中的一个重要内容,在数学分析、几何学、线性方程组理论、二次型理论等方面应用广泛。由于行列式的计算方法很多:利用n阶行列式的定义,把行列式化为上(下)三角形,按行(列)展开法则等,所以在计算行列式时,往往根据行列式自身的特点选择方法进行计算。而且不仅仅局限于某一种算法,主要根据其组成元素的规律寻找相应的计算方法。
方法一:按行(列)展开法则。
先把Dn按照第一行展开,得

再把Mn-1按照第一列展开,得
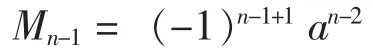
所以 Dn=an+(-1)2n+1an-2=an-an-2=an-2(a2-1).
方法二:化为下三角形。
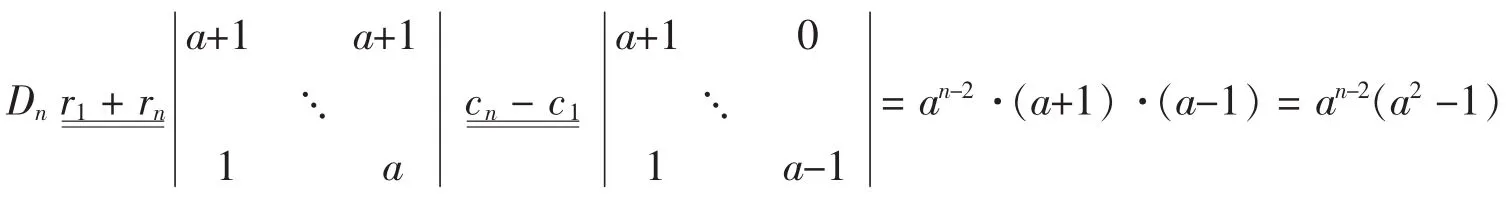
或者如下分两种情况讨论计算:
方法三:化为上三角形。
当a≠0时,

方法四:利用分块对角矩阵的行列式的计算方法。

方法五:递推降阶。
先把 Dn按照第二行展开,得 Dn=a·(-1)2+2Dn-1,再把 Dn-1按照第二行展开,得 Dn-1=a·(-1)2+2Dn-2,依次下去得 Dn=aDn-1=a2Dn-2= … =an-3D3=an-2D2=an-2(a2-1).
方法六:利用数学归纳法。
当n=2时,Dn=
当n=3时,Dn=
当n=4时,Dn=
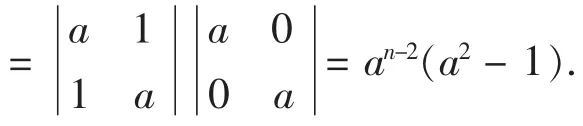
故猜测Dn=an-2(a2-1)下面利用数学归纳法证之。
假设当 n=k 时,Dk=ak-2(a2-1),下证 Dk+1=ak-1(a2-1).
把 Dk+1按照第 k 行展开, Dk+1=(-1)k+kDk= a·ak-2(a2-1)=ak-1(a2-1).
[1] 同济大学数学系.线性代数[M].北京:高等教育出版社,2007:9-27.
[2] 北京大学数学系几何与代数教研室.高等代数[M].北京:高等教育出版社,2007:68-83.
[3] 杨子胥.高等代数习题解[M].济南:山东科学技术出版社,2001:245-329.
[4] 毛纲源.线性代数解题方法技巧归纳[M].武汉:华中理工大学出版社,2000:3-10.
[5] 古家虹.关于行列式的计算方法[J].广西大学学报(自然科学版),2005,(S1):174-176.
[6] 张新功.行列式的计算方法探讨[J].重庆师范大学学报,2011,(4):88-92.
[7] 邓勇.关于行列式计算的另类降阶法[J].大学数学,2012,(6):102-108.
——丘成桐

