一类具有时滞的捕食系统的全局稳定性

刘 敏

（巢湖学院数学系，安徽 巢湖 238000）

1 引言

本文考虑的是具有时滞的Holling-I型功能反应的下列简化捕食者-食饵系统：

这里 x、y 分别表示食饵种群和捕食者种群的密度。 设其初始条件为 x0（θ）=φ1（θ）≥0， y0（θ）=φ2（θ）≥0，θ∈[-τ，0]，x（0）＞0，y（0）＞0，k0，k1，δ，β 均是正数，且考虑到模型的生物学意义，我们仅对其在内进行讨论。文[1]讨论了该捕食系统的解的有界性和持久性，并分析了正平衡点的局部稳定性和Hopf分支的存在性，给出了下述结论：

引理 1[1]当 t充分大时，系统（1）是最终有界的，有 x（t）≤k0，y（t）≤M，其中

引理2[1]当时，系统（1）是持久的。

引理 3[1]系统（1）的唯一正平衡点 E*（x*，y*）是条件稳定的，其中

这里0＜x*＜k0＜k1.

本文在上述结论基础上，主要对系统（1）的正平衡点E*的全局稳定性进行研究。

2 正平衡点的全局稳定性

由引理2及其证明，我们知当系统（1）是持久的，则其解满足m1≤x≤k0，m2≤y≤M，这里.下面我们将利用Liapunov方法来研究系统（1）的正平衡点E*的全局稳定性问题，给出下列结论：

定理 若系统（1）是持久的，并且满足：

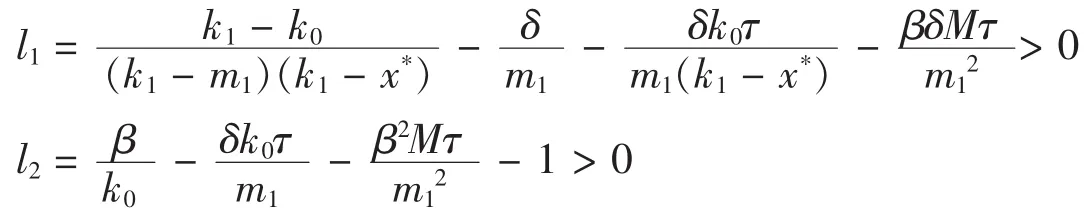
那么系统（1）的正平衡点 E*（x*，y*）是全局渐近稳定的。

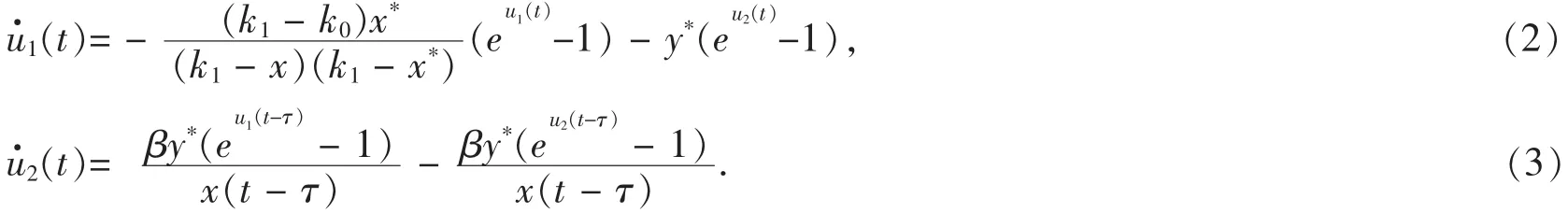
又由引理1和引理2，可知存在T＞0，使得t＞T时，有

由（3）式可得

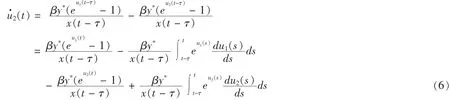
由（2）、（3）和（4），可得

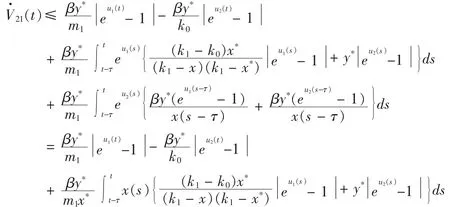
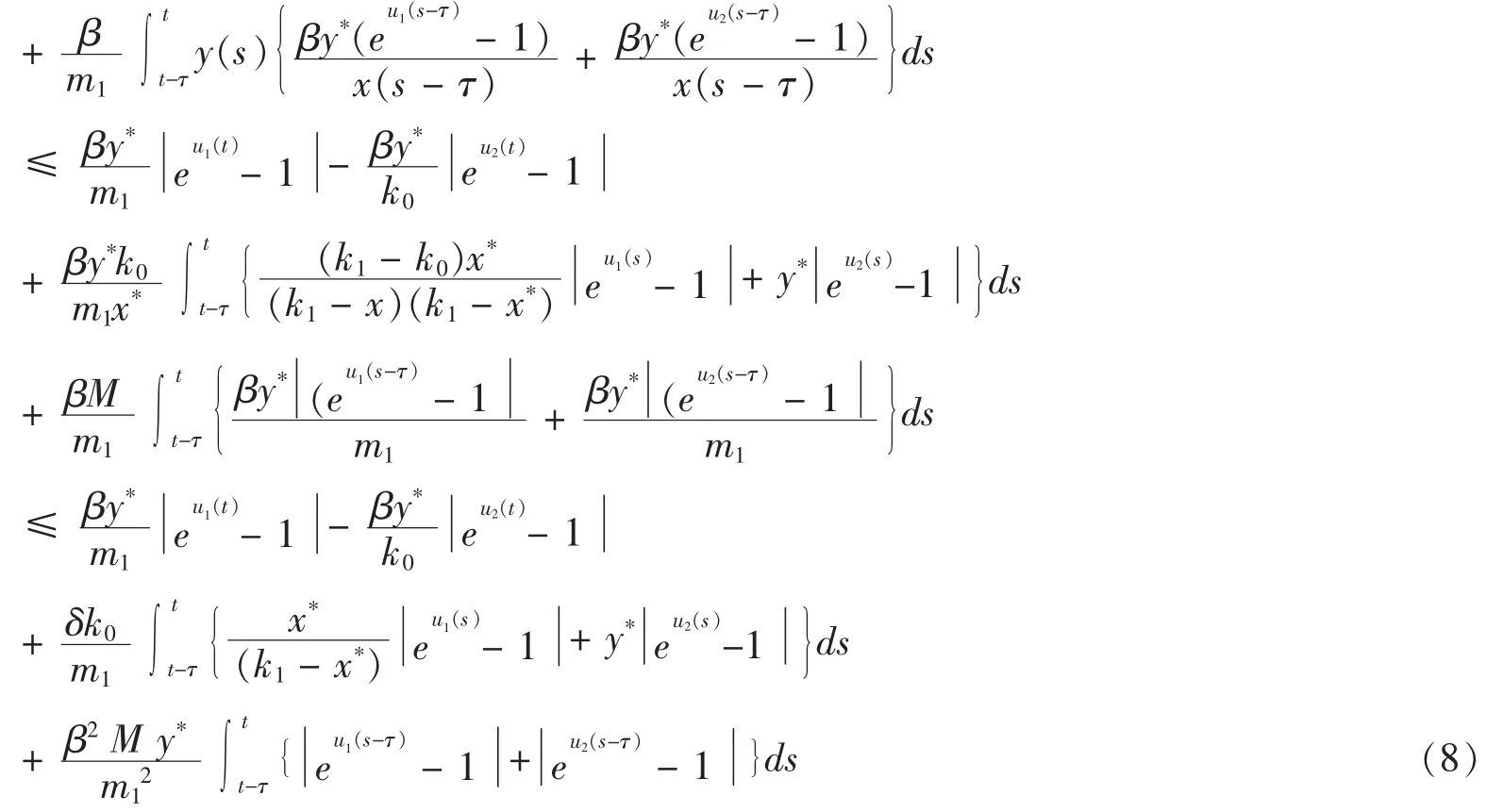
定义

从而有

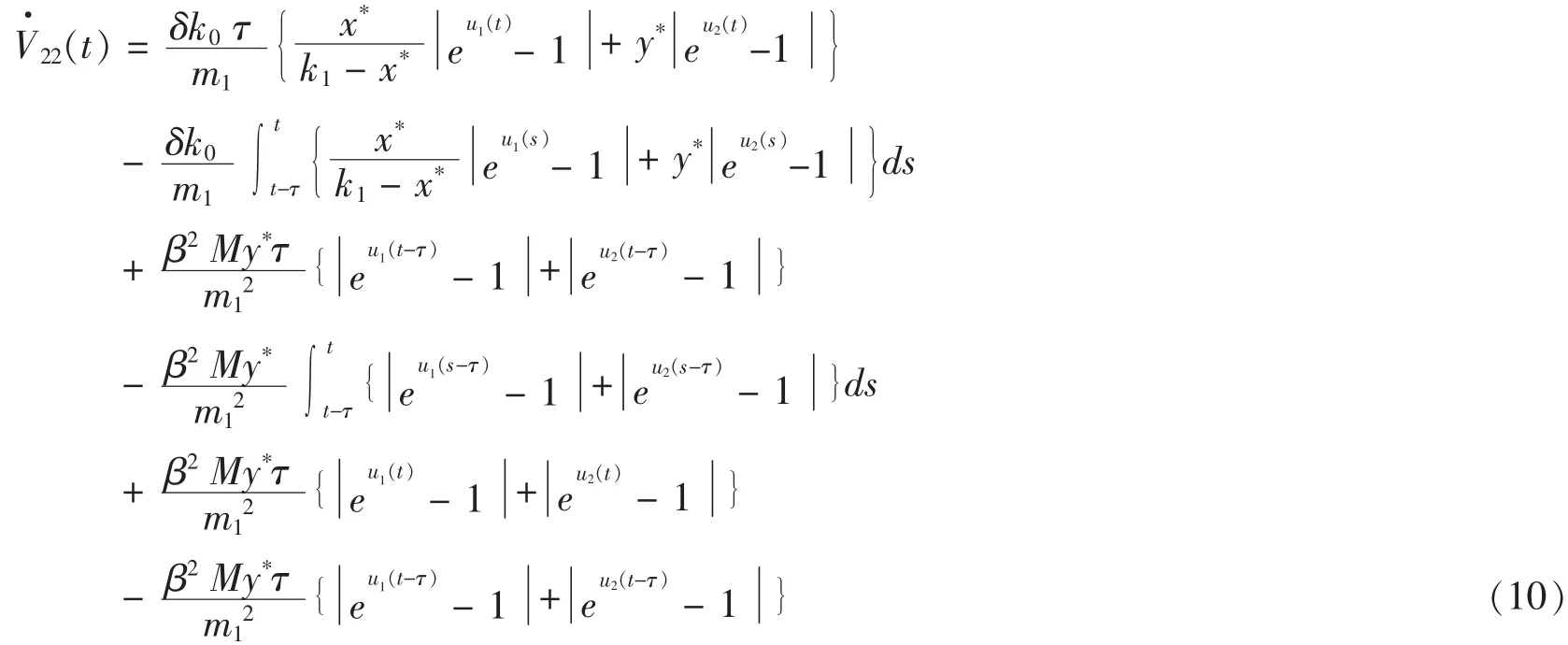
令 V2（t） =V21（t） +V22（t），则由（9）和（10）可得

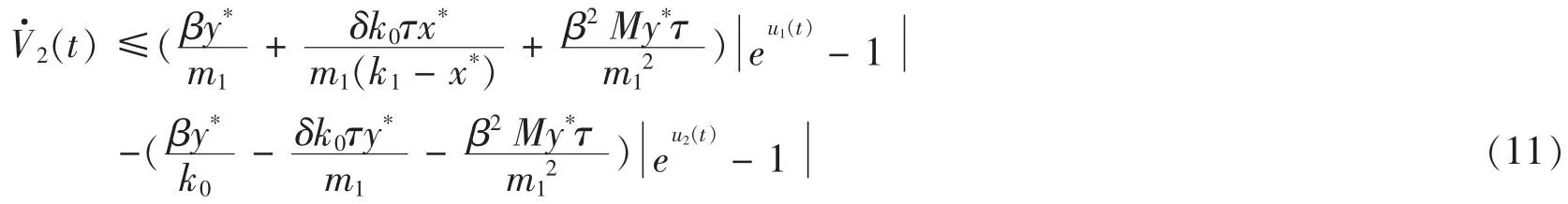
再令 V（t） =V1（t）+V2（t），则由（5）和（11）有

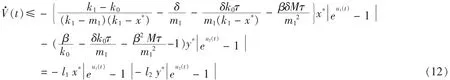
又由系统（1）的解具有持久性，可知存在T＞0，使得时t＞T，有

利用中值定理知，存在 0 ＜ θ1（t）＜ u1（t），0 ＜ θ2（t）＜ u2（t）使得

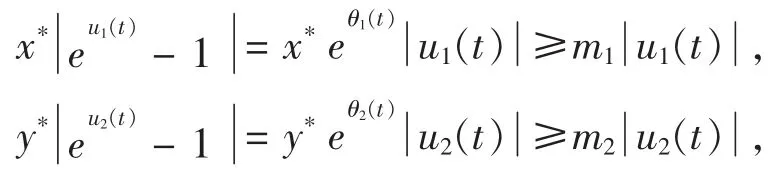
根据Liapunov稳定性定理，方程（2）-（3）的零解是全局渐近稳定的，由此可得系统（1）的正平衡点E*是全局渐近稳定的。

[1] 刘敏.一类具有时滞的捕食系统的持久性和Hopf分支的存在性[J].巢湖学院学报，2009，（3）：4-6.

[2] 李义龙,肖冬梅.具有非单调功能反应的捕食系统的定性分析[J].上海交通大学学报，2007，（5）：848-851.

[3] 尤秉礼.常微分方程补充教程[M].北京：人民教育出版社，1982.

[4] 马知恩.种群生态学的数学建模与研究[M].合肥：安徽教育出版社，1996.

[5] 马知恩,周义仓.常微分方程定性与稳定性方法[M].北京：科学出版社，2001.

[6] Lv S,Min Zhao.The dynamic complexity of a three species food chain model[J].Chaos，Solitons&Fractals,2008，（37）：1469-80.

[7] Sun Cheng jun,Lin Yi ping,Han Mao an.Stability and Hopf bifurcation for an epidemic disease model with delay[J].Chaos,Solitons&Fractals，2006，（30）：204-216.

[8] Zhiqi Lu,Xia Liu.Analysis of a predator-prey model with modified Holling-Tanner functional response and time delay[J].Nonlinear Analysis：Real Applications,2008，（9）：641-650.