Holling功能性反应的生态-流行病数值仿真
林梦醒
(广东工业大学应用数学学院,广东广州510520)
由于流行病必然在生态物种之间传播,因此近年来有学者把生态学和流行病动力学结合起来考虑。随着传染病已成为控制和调节人类与自然物种大小的一个重要因素,疾病在生态系统的影响也随之成为传染病研究的一个重要课题。数学模型方法在分析传染病的传播和控制方面已经变成相当重要的研究工具。
很多研究表明捕食者更易于捕食已染病食饵,从而使得捕食者物种患有疾病。将具有Logistic增长的捕食-食饵模型与食饵物种感染捕食者的流行病模型相结合可建立生态-流行病模型。已有一些相关理论研究成果,如:在捕食者患病的流行病模型[1]中考虑食饵具有Holling II功能性反应和捕杀效应,得到疾病是否流行的阈值和稳定条件。疾病在捕食者之间传播的流行病模型[2]考虑食饵具有三类Holling功能性反应和捕杀效应,捕食者具有饱和传染率的生态-流行病模型,得到疾病是否流行的阈值和稳定条件。食饵有病[3-5]且对食饵引入人工连续性捕杀效应的模型[6]并假设捕食者一旦染病就不再康复。还有疾病只在捕食者中传播的模型[7],捕食者染病的生态-流行病模型[8-13],疾病在两相互竞争物种中传播的模型[14],疾病在物种之间交叉感染的模型[15],均假设捕食者一旦染病就不再康复[14-15]。以上文献讨论了食饵和捕食者关系模型,但并没有讨论这类模型的数值仿真以及收敛性。本文研究具有Holling功能性反应以及人工捕杀效应生态-流行病模型数值仿真,并讨论对生态-流行病模型稳定性和收敛性的影响,生态-流行病模型数值仿真对生态学有指导意义,它对研究维持物种间的生态平衡具有重要意义。
1 三类功能性反应的生态-流行病模型
HollingI功能性反应的生态-流行病模型为
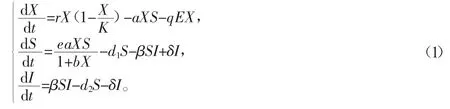
其中,X为食饵密度,S、I分别为易感类捕食者和染病类捕食者的密度;所有系数均为正常数,r为食饵的内禀增长率,K为食饵的环境容纳量,a为捕食系数,e(0<e≤1)为转化系数;d1为易感类捕食者的自然死亡率,d2为染病类捕食者的死亡率,则d2≥d1;β为感染率;δ为染病类捕食者的恢复率;E为对食饵的人工捕杀效力,qE为对食饵的有效捕杀力,aXS中的X是Holling I功能性反应函数。
系统(1)稳定,可以分为以下四种情况[2]:
1o当qE>r>0且K>X,食饵、易感捕食者和感染捕食者都趋于灭绝;
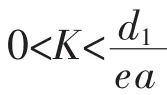
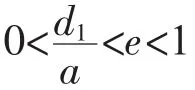
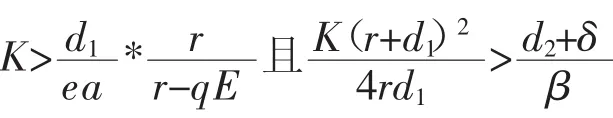
HollingII功能性反应的生态-流行病模型为
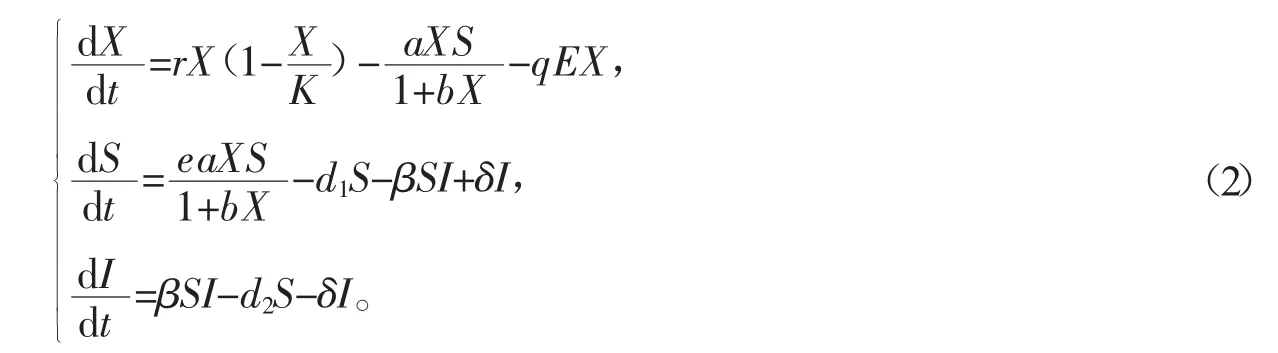
为便于讨论,这里模型(2)要求rea(Kb-1)<rbd1(Kb+1)+KbqE(ea-bd1)。
系统(2)稳定,可以分以下四种情况[1]:
1o当qE>r>0且K>X,食饵、易感捕食者和感染捕食者都趋于灭绝;
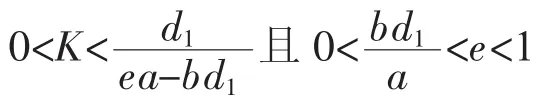
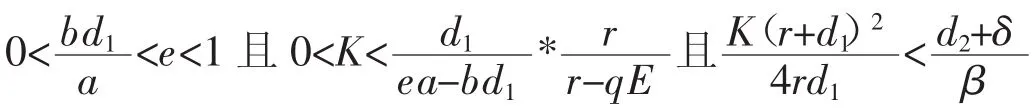
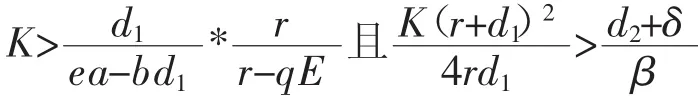
HollingIII功能性反应的生态-流行病模型为
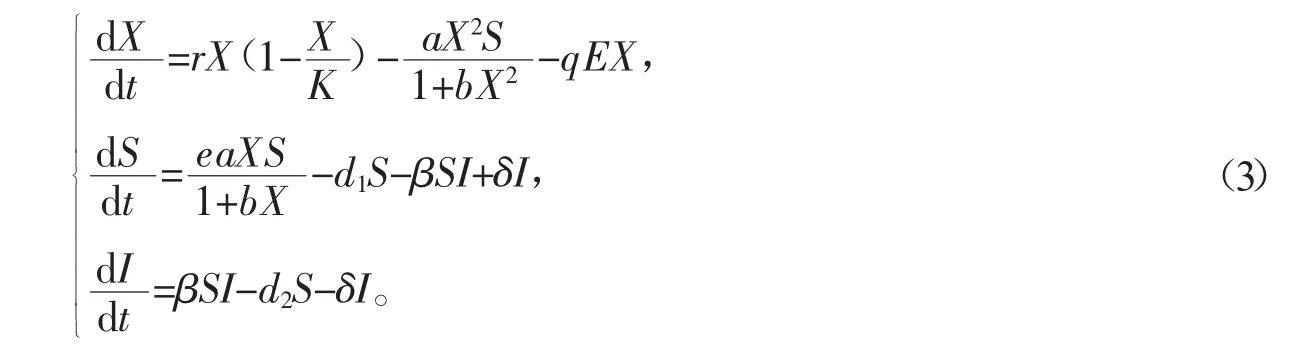
系统(3)稳定,可以分以下三种情况[2]:
1o当K>X且qE>r,食饵、易感捕食者和感染捕食者都趋于灭绝;
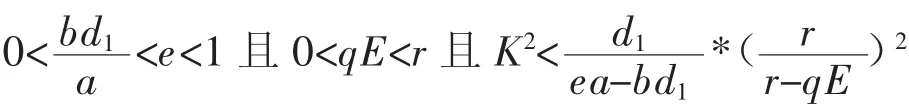
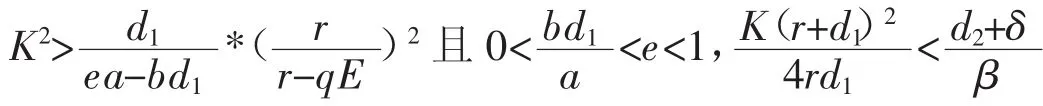
2 三类功能性反应的生态-流行病模型数值仿真
2.1 Holling I功能性反应的生态-流行病模型数值仿真
第1种情况数值仿真结果如图1所示。
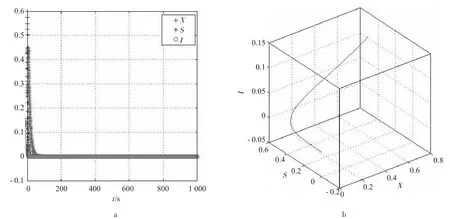
图1 系统(1)稳定的第1种情况
从图1可知,只要满足1o情况,其他参数在合理的范围任意变化,食饵X、易感捕食者S和感染捕食者I的密度都稳定于(0,0,0)一点,则食饵、易感捕食者和感染捕食者都趋于灭绝,系统(1)不收敛。
第2种情况数值仿真结果如图2所示。
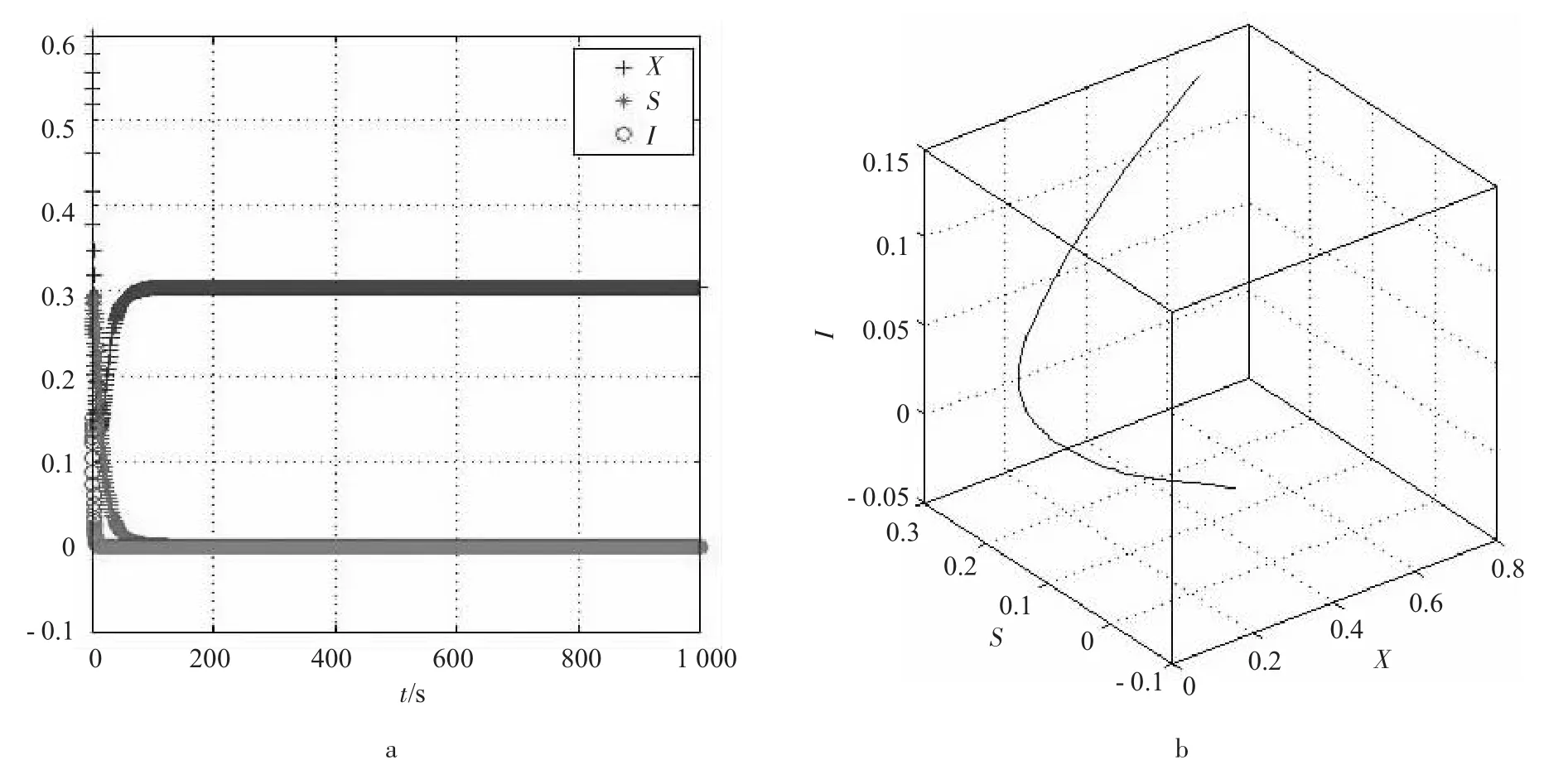
图2 系统(1)稳定的第2种情况
从图2可知,只要满足2o情况,其他参数在合理的范围内任意变化,食饵X、易感捕食者S和感染捕食者I的密度都稳定于(X,0,0)一类点,则食饵存在,易感捕食者和感染捕食者都趋于灭绝,系统(1)不收敛。
第3种情况数值仿真结果如图3所示。
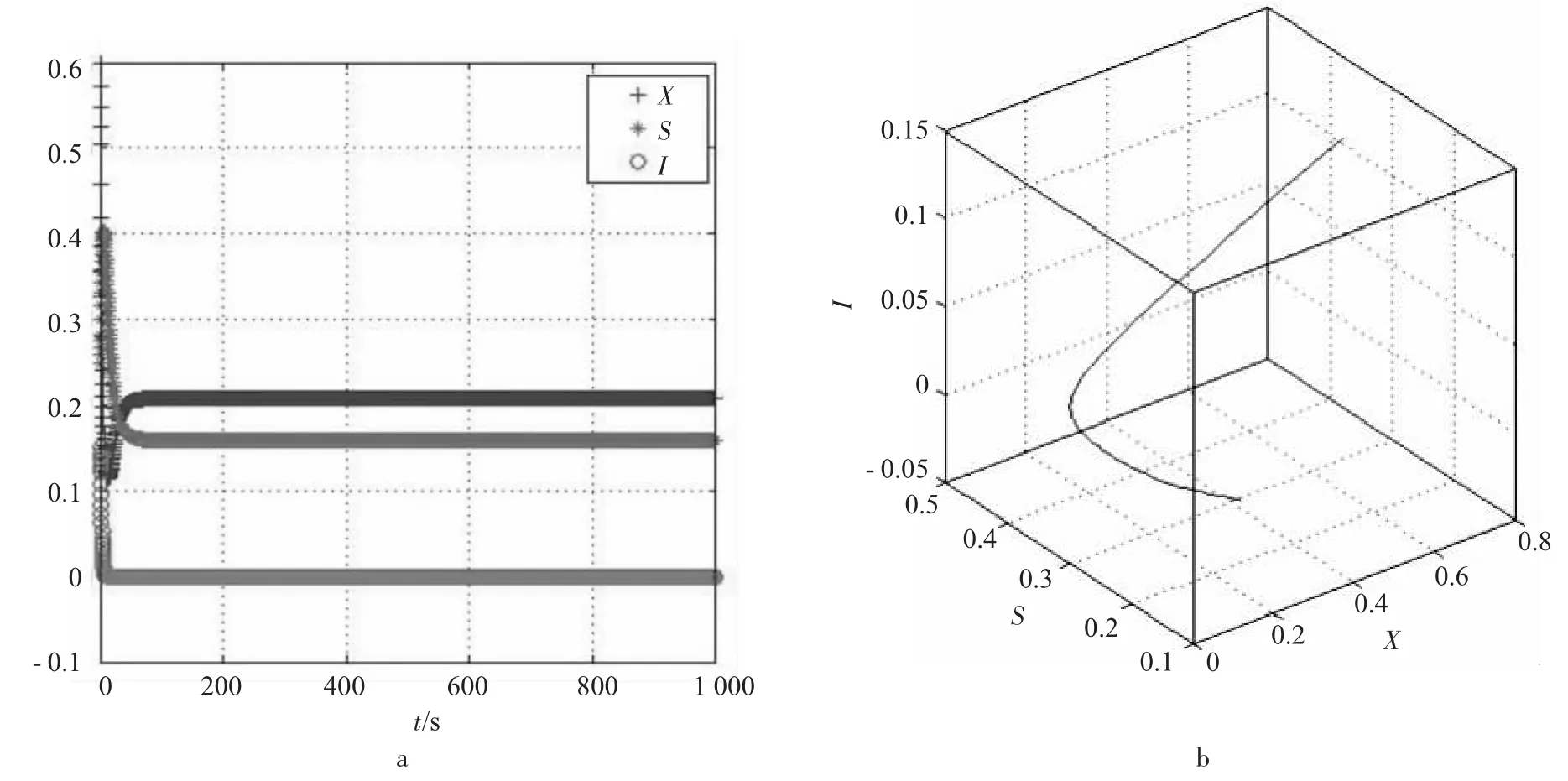
图3 系统(1)稳定的第3种情况
从图3可知,只要满足3o情况,其他参数在合理的范围任意变化,食饵X、易感捕食者S和感染捕食者I的密度都稳定于(X,S,0)一类点,则食饵和易感捕食者和谐共存,感染捕食者都趋于灭绝,系统(1)不收敛。
第4种情况数值仿真结果如图4所示。
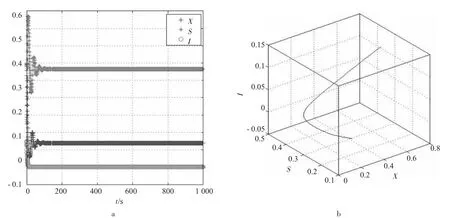
图4 系统(1)稳定的第4种情况
从图4可知,只要满足4o情况,其他参数在合理的范围任意变化,食饵X、易感捕食者S和感染捕食者I的密度都稳定于(X,S,0)一类点,则食饵和易感捕食者和谐共存,感染捕食者都趋于灭绝,系统(1)收敛。
2.2 Holling II功能性反应的生态—流行病模型数值仿真
第1种情况数值仿真结果如图5所示。
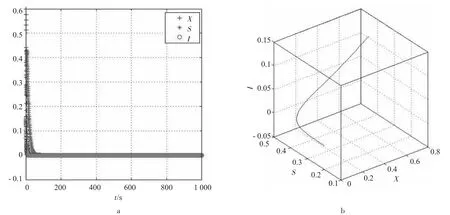
图5 系统(2)稳定的第1种情况
从图5可知,只要满足1o情况,其他参数在合理的范围任意变化,食饵X、易感捕食者S和感染捕食者I的密度都稳定于(0,0,0)一点,则食饵、易感捕食者和感染捕食者都趋于灭绝,系统(2)不收敛。
第2种情况数值仿真结果如图6所示。
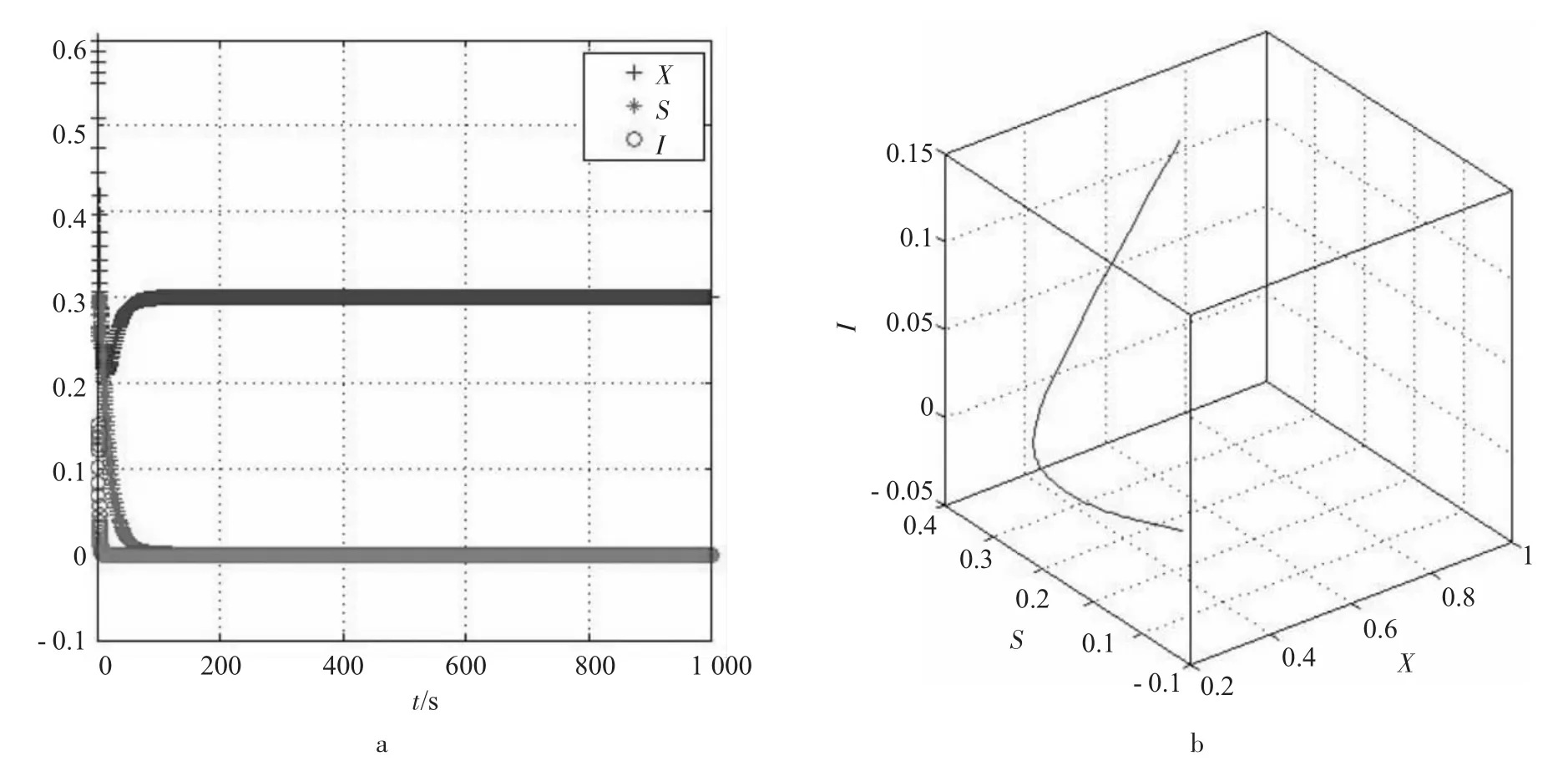
图6 系统(2)稳定的第2种情况
从图6可知,只要满足2o情况,其他参数在合理的范围内任意变化,食饵X、易感捕食者S和感染捕食者I的密度都稳定于(X,0,0)一类点,则食饵存在,易感捕食者和感染捕食者都趋于灭绝,系统(2)不收敛。
第3种情况数值仿真结果如图7所示。
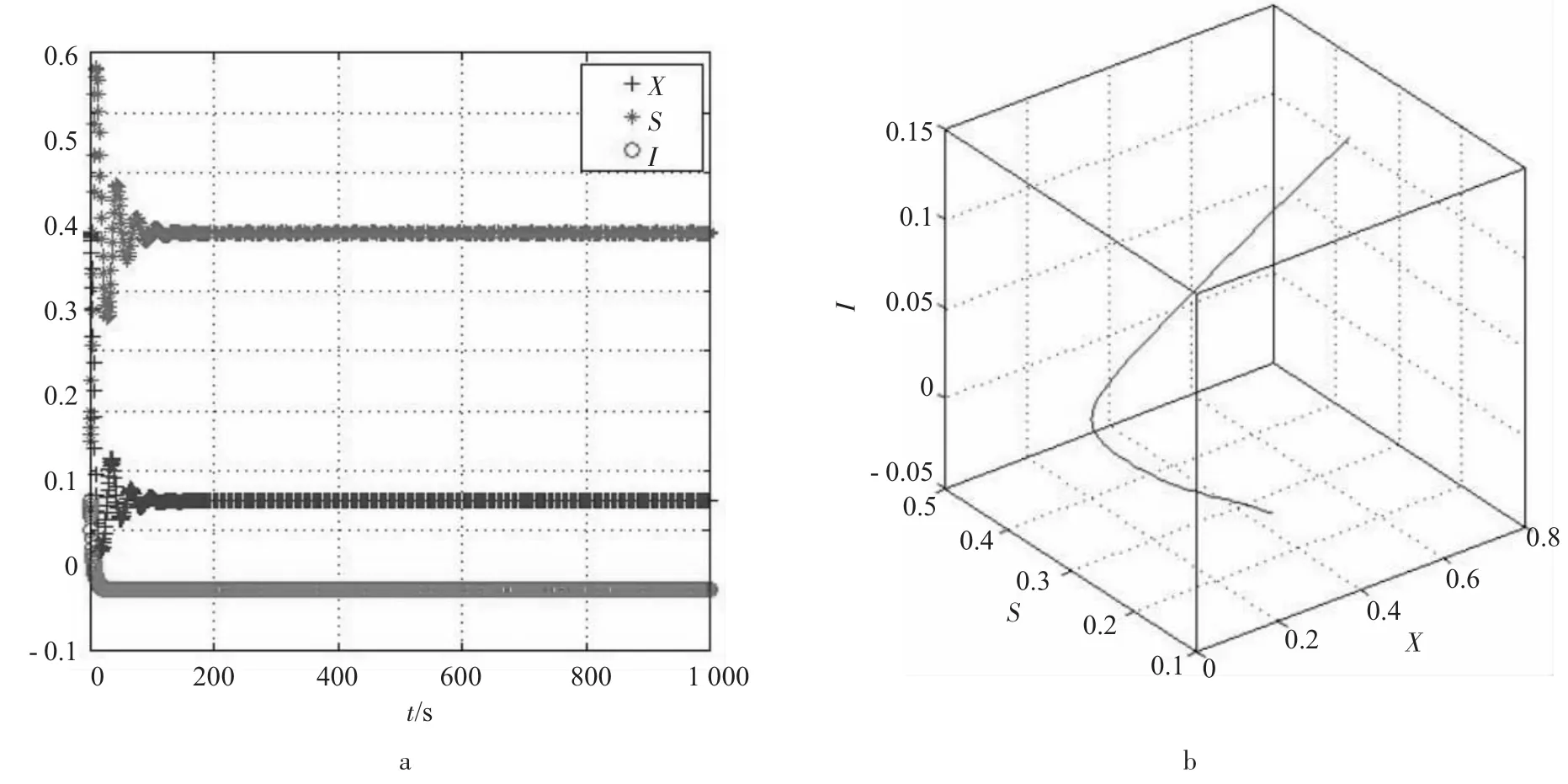
图7 系统(2)稳定的第3种情况
从图7可知,只要满足3o情况,其他参数在合理的范围任意变化,食饵X、易感捕食者S和感染捕食者I的密度都稳定于(X,S,0)一类点,则食饵和易感捕食者和谐共存,感染捕食者都趋于灭绝,系统(2)不收敛。
第4种情况数值仿真结果如图8所示。
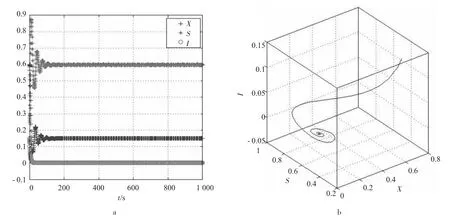
图8 系统(2)稳定的第4种情况
从图8可知,只要满足4o情况,其他参数在合理的范围任意变化,食饵X、易感捕食者S和感染捕食者I的密度都稳定于(X,S,0)一类点,则食饵和易感捕食者和谐共存,感染捕食者都趋于灭绝,系统(2)收敛。
2.3 Holling III功能性反应的生态-流行病模型数值仿真
第1种情况数值仿真结果如图9所示。
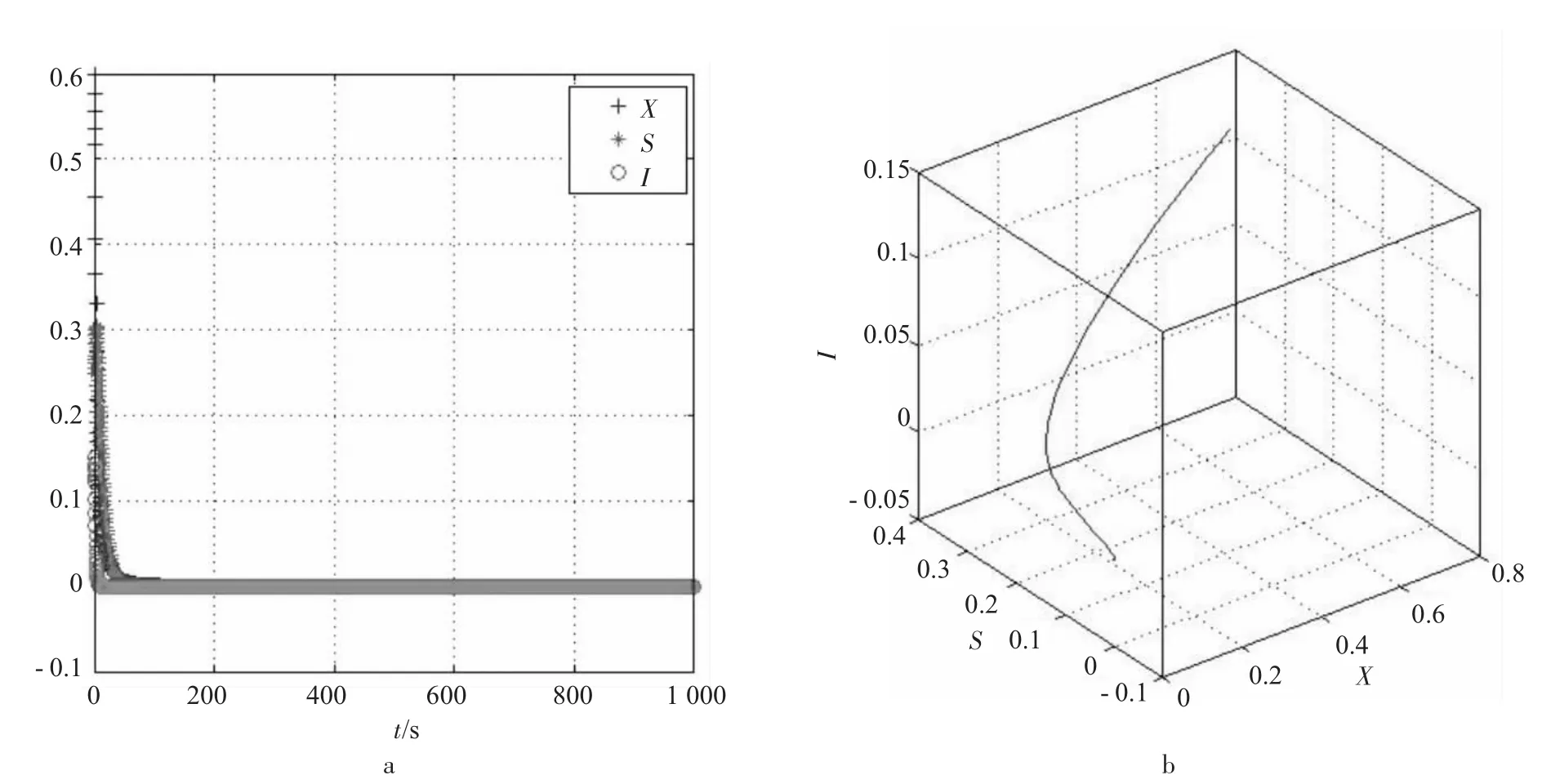
图9 系统(3)稳定的第1种情况
从图9可知,只要满足1o情况,其他参数在合理的范围任意变化,食饵X、易感捕食者S和感染捕食者I的密度都稳定于(0,0,0)一点,则食饵、易感捕食者和感染捕食者都趋于灭绝,系统(3)不收敛。
第2种情况数值仿真结果如图10所示。
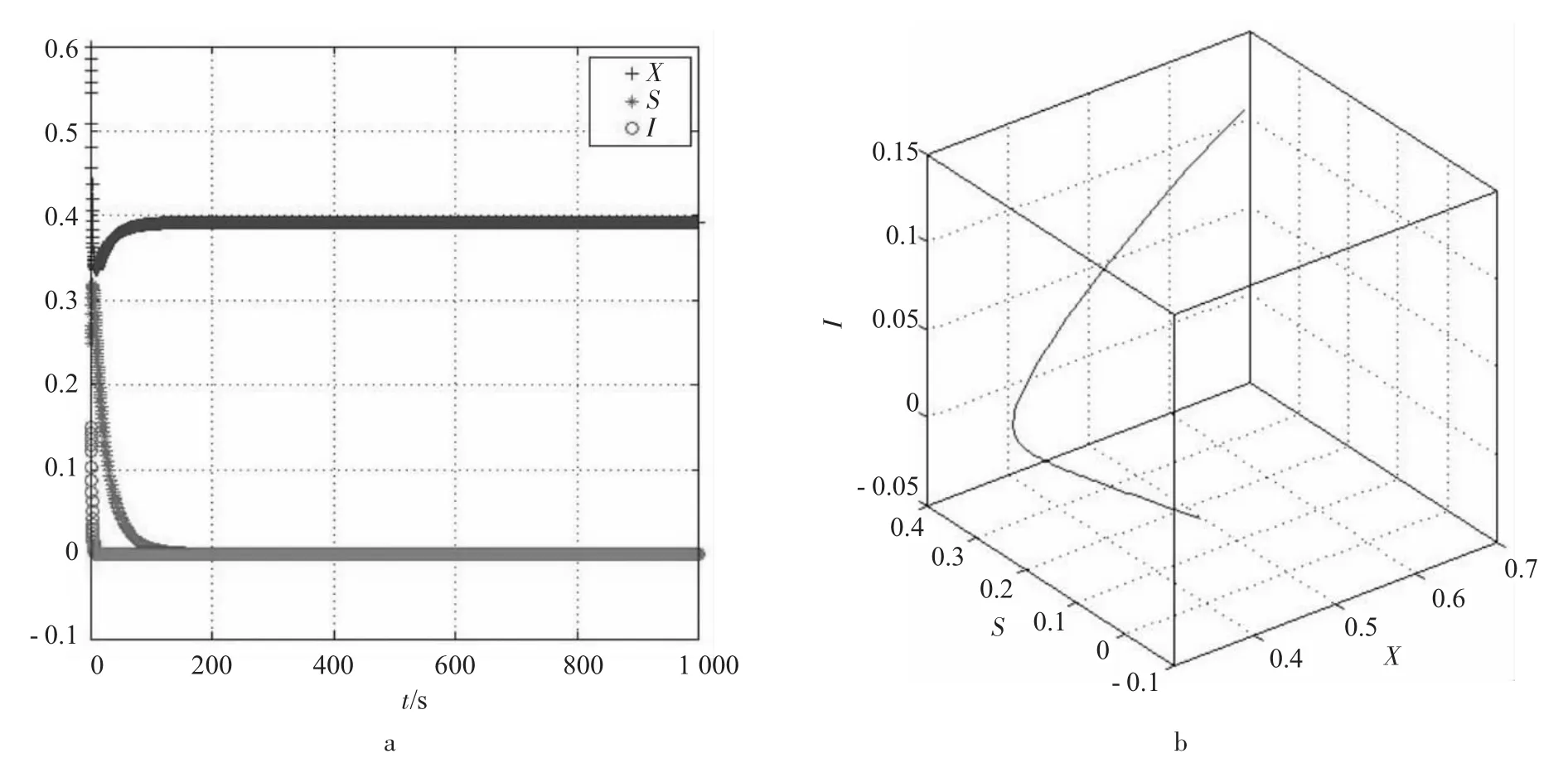
图10 系统(3)稳定的第2种情况
从图10可知,只要满足2o情况,其他参数在合理的范围任意变化,食饵X、易感捕食者S和感染捕食者I的密度都稳定于(X,0,0)一类点,则食饵存在,易感捕食者和感染捕食者都趋于灭绝,系统(3)不收敛。
第3种情况数值仿真结果如图11所示。
图11 系统(3)稳定的第3种情况
从图11可知,只要满足3o情况,其他参数在合理的范围任意变化,食饵X、易感捕食者S和感染捕食者I的密度都稳定于(X,S,0)一类点,则食饵和易感捕食者和谐共存,感染捕食者都趋于灭绝,系统(3)不收敛。
3 结论
本文数值仿真结果表明,qE与r的关系对三类Holling功能性反应的生态-流行病模型的稳定性有影响。当 qE>r>0 且 K>X,在 Holling I、Holling II、Holling III功能性反应的生态-流行病模型中,食饵、易感捕食者和感染捕食者的密度都趋于灭绝,稳定于(0,0,0),但系统不收敛;当0<qE<r且K>X且满足参数在一定的范围内,在Holling I、Holling II、Holling III功能性反应的生态-流行病模型中,食饵存在,易感捕食者和感染捕食者都趋于灭绝,稳定于(X,0,0),但系统不收敛;当0<qE<r且K>X且满足参数在一定的范围内,在Holling I、Holling II、Holling III功能性反应的生态-流行病模型中,食饵和易感捕食者和谐共存,感染捕食者趋于灭绝,稳定于(X,S,0),但系统不收敛;当0<qE<r且K>X且满足参数在一定的范围内,在Holling I、Holling II功能性反应的生态-流行病模型中,感染捕食者趋于灭绝,稳定于(X,S,0),但系统收敛。

