关于集列极限的基本性质
李学东
(佛山市数学学会,广东佛山528000)
在数学分析中,数列极限的一些基本性质揭示了数列极限存在的确定性条件以及不同数列之间项的大小关系对它们极限大小关系的影响[1]。类似地,关于集合列的极限也有相应的对应性质,这些性质同样揭示了集合列的极限存在的确定性条件以及不同集合列之间项的包含关系对它们极限包含关系的影响[2]。关于集列极限的定义与运算在文献[3]中已有论述。
为表述方便,我们约定“⊆”表示“包含于”,“⊂”表示“真包含于”。对于“⊇、⊃”作类似区分。
定理1若集列收敛,则它的集限是唯一的。
证明 设{An}为一收敛数列,若它收敛于两个不同的集限A、B,即
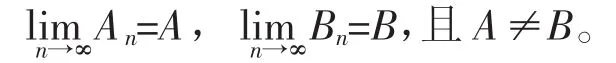
由于A≠B,所以(A-B)∪(B-A)≠Ø。
不妨设 B-A≠Ø,则∃x0∈(B-A)使得 x0∈B,x0∈A。从而有 x0∉(An∩A),x0∈(An∪B)。
由 x0∉(An∩A)知 x0∉(An∪A),所以 x0∉An。
同理:对于 x0∈B,∃K2>0,当 n>K2时,x0∉‖An-B‖,即 x0∉[(An∪B)-(An∩B)]。
由 x0∈(An∪B)知 x0∈(An∩B),所以 x0∈An。
取 K=max(K1,K2),则当 n>K 时,x0∉An、x0∈An同时成立。这和“元素与集合的关系”相矛盾,所以假定A≠B不成立。故A=B。亦即定理1成立。
考虑到 x∈A,可知:当 n>K1时,x∈An。又知∀n∈N,An⊆Bn,所以当 n>K1时,有


取 K=max(K1,K2),则当 n>K 时,式(1)、(2)同时成立。所以 x∈(Bn∪B)⇒x∈(Bn∩B)⇒x∈B,A⊆B。故定理2成立。
在定理2中,若∀n∈N,An⊂Bn,A⊂B不一定成立。
在lim An=A,lim Bn=B的前提下,如果定理2中的条件∀n∈N,An⊆Bn与结论A⊆B互换,则命题不再成立。
在定理2中的逆命题虽然不成立,但若再添加一些条件,则有如下定理:
定理 3 对于集列{An}、{Bn},∀n∈N,An∩Bn=An或 Bn,且。若 A⊂B,则∃K>0,当 n>K 时,恒有 An⊂Bn。
证明 设全集为 U,已知 A⊂B,所以∃x0∈U使得 x0∈B且 x0∉A。从而∀n∈N,x0∉An∩A,x0∈Bn∪B。
考虑到∀n∈N,x0∉An∩A,所以 x0∉An∪A,于是当 n>K1时 x0∉An。
考虑到∀n∈N,x0∈Bn∪B,所以 x0∈Bn∩B,于是当 n>K2时 x0∈Bn。
取 K=max(K1,K2),则当 n>K 时有 x0∉An且 x0∈Bn,又∀n∈N,An∩Bn=An或 Bn,所以当 n>K 时恒有An⊂Bn,证毕。
满足条件“∀n∈N,An∩Bn=An或Bn”的两个集列{An}、{Bn}可视为同一单调集列中的两个子集列,我们称之为同调集列。如度量空间Rn中的同心球域簇及数轴上关于0点对称的连续区间簇所构成的拓扑空间中任意两个序列都是同调集列。
关于定理3有如下两个推论:
推论 1 对于集列{An},∀n∈N,An∩B=An或 B,且,若 A⊂B,则∃K>0,当 n>K 时,恒有An⊂B。
推论 2 对于集列{An},∀n∈N,An∩B=An或 B,且,若 A⊃B,则∃K>0,当 n>K 时,恒有An⊃B。
这两个推论不难证明,在定理3中∀n∈N只需令Bn=B即可。
与数列极限中的两边夹定理类似,在集列的集限中也有相应的定理。
定理 4 对于集列{An}、{Bn}、{Cn},∃K0>0,当 n>K0时,恒有 An⊆Bn⊆Cn,若,则有。
证明 设全集为U,∀x∈U。
(1)若 x∈H,则 x∈(An∪H)(n∈N)。因为,所以∃K1>K0>0,当 n>K1时,x∉‖An-H‖,即x∉[(An∪H)-(An∩H)]。由 x∈(An∪H)知 x∈(An∩H),于是 x∈An。
考虑到:当 n>K1时 An⊆Bn⊆Cn恒成立,所以当 n>K1,有 x∈Bn,从而 x∈(Bn∩H);当 n>K1时,x∉‖Bn-H‖。
(2)若 x∉H,则 x∉(Cn∩H)(n∈N)。因为 lim Cn=H,所以∃K2>K0>0,当 n>K1时,x∉‖Cn-H‖,即x∉[(Cn∪H)-(Cn∩H)]。由 x∉(Cn∩H)知 x∉(Cn∪H),于是 x∉Cn。
考虑到:当 n>K2时 An⊆Bn⊆Cn恒成立,所以当 n>K2时,有 x∉Bn,从而 x∉(Bn∪H);当 n>K2时,x∉‖Bn-H‖。
综合(1)(2)所述:取 K=max(K0,K1,K2),则当 n>K 时,∀x∈U 总有 x∉‖Bn-H‖成立。故。
证明 设全集为U。
(3)取 K=max(K1,K2),则当 n>K 时,y0∈Bn但 y0∉B,x∈(An∩A)可同时成立。此时(x,y0)∈An×Bn,但是(x,y0)∉A×B,所以(x,y0)∈[(An×Bn)∪(A×B)-(An×Bn)∩(A×B)],即 当 n>K 时总会有(x,y0)∈‖(An×Bn)-(A×B)‖。

