一类七次系统三次幂零奇点的焦点判定与极限环分支
卜珏萍
(巢湖学院数学系,安徽 巢湖 238000)
讨论一类七次微分自治系统

其中原点为三次幂零奇点,由文[1],容易验证,系统(1)中原点为中心或焦点。
由文[4]中给出的递推公式,利用Mathematica计算求得系统(1)原点的前10个拟Lyapunov常数如下:
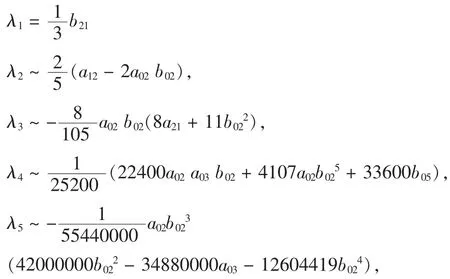

由 λ10≠0,可得

再由λ1=λ2=λ3=λ4=λ5=λ6=λ7=λ8=λ9=0得:
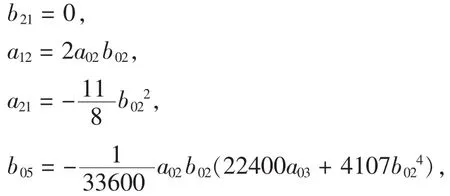

由于 a02≠0,b02≠0 时,
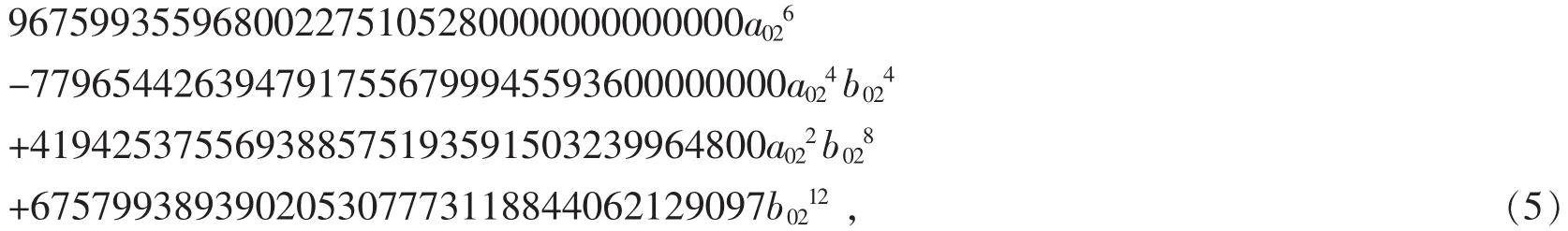
与

不能同时为零,即式(5)为零时,(6)不能为零,即当 λ9=0 时,λ10≠ 0,由此可得
定理1 系统(1)的原点为10阶细焦点的充要条件是
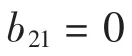

对系统(1)作微小扰动后的系统
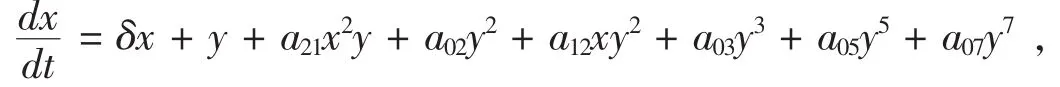

由定理 1,当充要条件(7)成立时,有
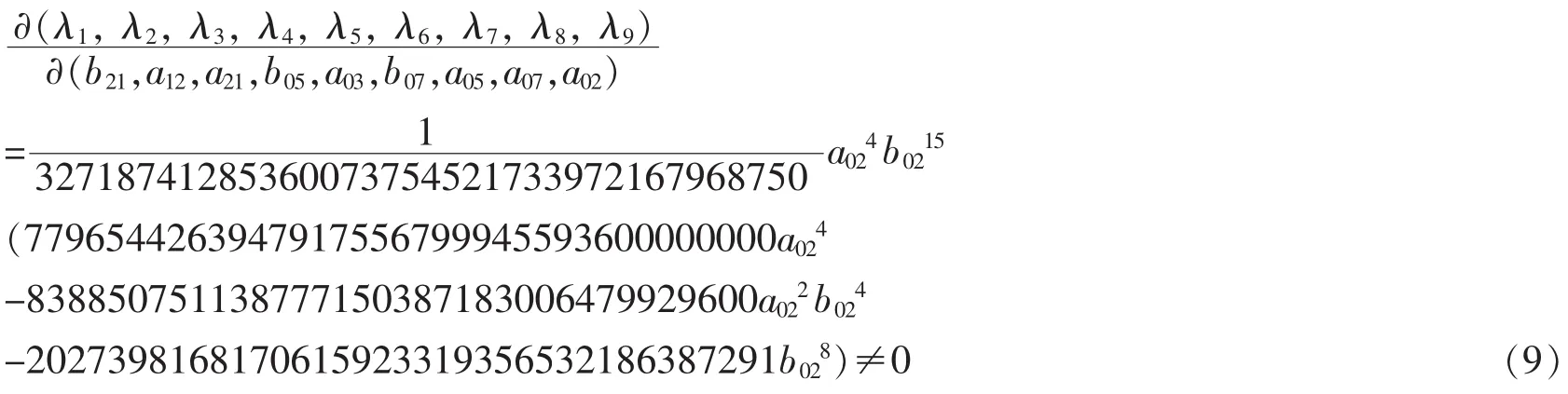
从而有
定理2 若系统(1)的原点为10阶细焦点,则当0<δ≪1,且系统(1)的系数作适当微小扰动时,系统(8)在原点的充分小邻域内恰有10个包围初等结点O(0,0)的极限环。
[1] Amelikin.B.B.,Lukashivich.H.A.,Sadovski.A.P.,Nonlinear Oscillations in Second Systems[M].Russian:BGY Lenin.B.I.Press.1982.
[2] Alvarez.M.J.,Gasull.A.,Monodrama and stability for nilpotent critical points[J].IJBC.2005,(4):1253-1265.
[3] Alvarez.M.J.,Gasull.A.,Cenerating limits cycles from a nilpotent critical point via normal forms[J].J.Math.Anal.Appl,2006,(318):271-287.
[4] 刘一戎,李继彬.平面向量场的若干经典问题[M].北京:科学出版社,2010.
[5] 徐玲,刘一戎.一类四次系统幂零中心焦点判定与极限环分支[J].丽水学院学报,2011,(2):1-5.
[6] 赵倩倩,刘贵兰.一类原点为幂零奇点的七次系统的焦点判定与极限环分支[J].佳木斯教育学院学报,2012,(3):144-145.

