不同孪晶界密度银纳米线拉伸形变行为的分子动力学模拟

孙 倩 杨熊博 高亚军 赵健伟

(南京大学化学化工学院,生命分析国家重点实验室,南京210008)

1 引言

金属纳米线的研究在基础物理学、微纳器件1和材料学等方面占有重要地位,是材料物理化学的重要分支.金属纳米线特殊的机械性质、2,3光电性质、4热力学性质5,6和磁性7等使其具有广泛的应用价值.构建高强度纳米线是研究的热点,孪晶界对金属纳米材料的物理化学性质影响显著,因此研究孪晶对纳米线形变的影响至关重要.

在实验研究方面,目前研究较多的是观察孪晶对[111]晶向的铜、银和金纳米线强度的影响.8-10Lu等11-14用脉冲电沉积技术制备出铜孪晶结构样品,并说明孪晶结构能进一步提升纳米材料的机械性能,随着孪晶层间距的减小,纳米孪晶铜的强度逐渐提高,最终拉伸强度可达1.07 GPa.Zhong等15用电沉积的方法制备的[111]孪晶纳米线,比相同尺寸的多晶铜纳米线的强度明显提高,从微电子器件方面展现了广泛的应用前景.Marszalek等16通过扫描探针显微镜(SPM)直接观测了2 nm亚单元内的金纳米线在[111]晶面上堆垛层的产生,这种堆垛层在分子动力学计算的塑性形变中都能观测到.Wu等17在实验上利用原子力显微镜(AFM)研究了含孪晶界的银纳米线弯曲形变,研究表明孪晶界阻碍了滑移的发展.Greer等18发现纳米尺度下单晶金纳米柱的强度是块状金的50倍左右,这主要就是因为位错源的匮乏引起的强度增加,这种现象的控制机制称为位错匮乏理论.

在理论模拟方面,用分子动力学方法研究在拉伸载荷下晶界对纳米线形变的影响被广泛报导.近年来,研究不同纳米材料的拉伸形变机理受到重视.19-22相关研究表明,孪晶Al纳米线的拉伸形变机理23是由孪晶界向相邻孪晶扩散.Yamakov等24模拟了铝纳米孪晶中位错间以及位错与孪晶界之间的相互作用,发现位错间以及位错与孪晶界之间会形成复杂的“位错网”,使位错大量堆积,从而强化纳米线.Jin等25研究了面心立方晶体中螺形位错与孪晶界的多种相互作用,在不同材料和应变量下,发现螺旋位错会经过相邻的孪晶界继续发展,或者被位错阻挡.Cao和Wei26,27用分子动力学模拟了纳米孪晶铜在受单向均匀拉伸载荷下的变形机制和含五个孪晶界纳米线的机械性质,发现孪晶对位错滑移具有阻挡作用,使得孪晶纳米线得到强化.Afanasyev和Sansoz28通过分子动力学方法研究了在压缩载荷下金纳米线中晶界对形变的影响,结果表明单晶纳米线的位错直接滑移到表面,而引入晶界之后,晶界通过形成滑移面与其它位错滑移相交,阻碍了位错直接滑移到纳米线的表面,实现了纳米线的强化.Zhang和Huang29通过分子动力学拉伸形变研究说明晶界并不总使得纳米线得到强化,根据得到的计算结果他们认为纳米线的自由表面决定着晶界对纳米线起到强化还是软化作用.Zhang等30通过分子动力学对含孪晶的铜纳米线的研究结果表明,在拉伸载荷作用下,孪晶界间距越小,纳米线在塑性形变区域内的应力越低.袁林等31用分子动力学方法模拟了不同晶粒尺寸下多晶银纳米线的拉伸变形行为,发现当晶粒尺寸小于13.49 nm时,多晶Ag纳米线呈现软化现象,出现反Hall-Petch关系.Gao等32通过分子动力学研究了五重孪晶银纳米线的拉伸和扭转形变行为,研究发现孪晶界可以强化纳米线,而且孪晶厚度越小,强化效应越明显.

迄今,关于孪晶界对金属纳米线形变的影响仍不清晰.孪晶纳米线机械性质变化的主要原因,是由于孪晶的相互作用和孪晶距的不同而导致位错,还是孪晶界阻挡位错滑移从而导致位错塞积,需进一步研究.为了解孪晶界对纳米线增强增韧的内在机制,很多学者在实验和理论方面进行了大量研究,但对孪晶界、自由表面、拉伸速度和温度等因素的综合影响研究较少.

本文将利用分子动力学模拟研究孪晶界密度对银纳米线强度及形变机理的影响,比较晶粒大小不同的纳米线与完美单晶纳米线的变形行为.并进一步考察孪晶界密度和表面对纳米线力学性能和塑性变形机理的共同影响,同时探讨温度和拉伸速度对纳米线屈服应力的影响,为构建高强度纳米线打下基础.

2 模拟方法

本文研究[111]晶向的孪晶银纳米线和完美单晶银纳米线的力学行为.其初始构型中原子按照理想的面心立方结构排布,截面是正方形.按照孪晶界密度的不同共建立八个银纳米线模型,纳米线的尺寸为6 nm×6 nm×23 nm,包含的孪晶界个数分别为1、2、3、5、15、23和47,孪晶界间距分别为11.334、7.556、5.667、3.778、1.417、0.945和0.472 nm.以含有五个孪晶界的银纳米线为例,图1给出其初始构型.该模型约含65000个原子,两端各有三层原子的固定层.图1(a)中绿色的原子表示面心立方原子和表面原子,红色的原子平面是孪晶界原子.图1(b)仅给出了棱角原子,即图中绿色原子和孪晶界原子.为了更好地模拟真实体系,计算中在x、y和z方向采用了自由边界条件.采用Nose-Hoover方法33,34进行等温调节,保持体系的温度为10 K.数值积分方案采用传统的蛙跳法.原子之间的相互作用采用多体势中的镶嵌原子势(EAM)35来描述.

首先使体系在10 K温度下自由弛豫20000步,当体系达到平衡状态以后,沿纳米线的长轴(z轴)以1.056×108s-1的应变速率匀速双向拉伸.拉伸过程中固定层仅沿z方向移动,其余原子可以自由运动.选择弛豫20000步以后再拉伸至断裂.

全部运算基于自主开发的大规模分子动力学仿真程序NanoMD,36该软件的可靠性不仅通过大量的规模研究,如改变体系的大小、37拉伸速率38,39等得以证实,同时模拟结果也与实验测量结果40,41相一致.

3 结果分析

3.1 模型的晶体学特点

为了考查晶体结构对纳米线拉伸形变的影响,对本文中所有模型的晶体学特点进行了统计,如表1所示.单晶纳米线长22.67 nm,约是截面边长的4倍,含有两个孪晶的纳米线每个晶粒的长度也有11.33 nm,远大于截面边长.只有当含有三个孪晶时,晶粒的长宽之比才接近1.含有四个以上孪晶时,晶粒在z方向上的尺寸显著小于x和y方向上的尺寸.这一结构特点将对位错的产生和滑移的发展产生影响.

本文中的单晶银纳米线是面心立方晶体结构以[111]晶向按…ABCABC…顺序堆垛而成.孪晶银纳米线在孪晶界上下呈镜面对称的孪晶关系,按…ABCA[B]ACBA…顺序堆垛而成,以[B]层为孪晶界,如图2所示.孪晶界原子与总原子数之比从1%至接近50%,但晶界原子仅仅改变了ABC周期排列的顺序,每个原子的平均能量并无显著差异.因此,结构差异是滑移的产生和发展的主要影响因素,但其对弹性形变,即位错产生前的纳米线强度无影响.

3.2 形变过程的宏观性质分析

由于尺寸的原因金属纳米线表现了与体相材料不一样的力学性质,金属纳米材料的机械性质是一个非常重要的性质,包括材料的屈服强度、应力应变以及杨氏模量等.金属纳米线的力学性质主要通过应力应变曲线和杨氏模量来分析,图3所示为不同孪晶界密度下银纳米线拉伸的应力应变曲线.拉伸的初始阶段为弹性变形,随着应变量的增加,拉伸应力线性上升至一峰值,即屈服点,屈服点所对应的应力叫做屈服应力,应变为屈服应变.之后,纳米线进入塑性形变区域,应力释放.应力呈波动变化直至纳米线断裂,应力趋近于零.拉伸使得原子脱节到新的位置,之后又结晶在一起,原子不断脱节和重结晶,造成了应力的波动.

导出的参数在图4中给出.在弹性形变区域内,金属纳米线的晶格结构对纳米线的强度起作用,晶界作用不明显.由图4(a)可看出,具有一个、两个和三个孪晶界的纳米线的屈服应力分别为3.0、3.5和4.0 GPa.作为对比,单晶银纳米线的屈服应力为4.2 GPa.而具有五个、十五个、二十三个和四十七个孪晶界的纳米线的屈服应力则大于单晶银纳米线,其值分别为5.1、6.2、6.7和7.0 GPa.当孪晶界间距小于6.0 nm时,随着间距的减小,纳米线的屈服应力近似地呈线性增加.图4中阴影部分的误差带表示单晶多次计算的值为(4.1±0.1)GPa,相对偏差为2.4%.

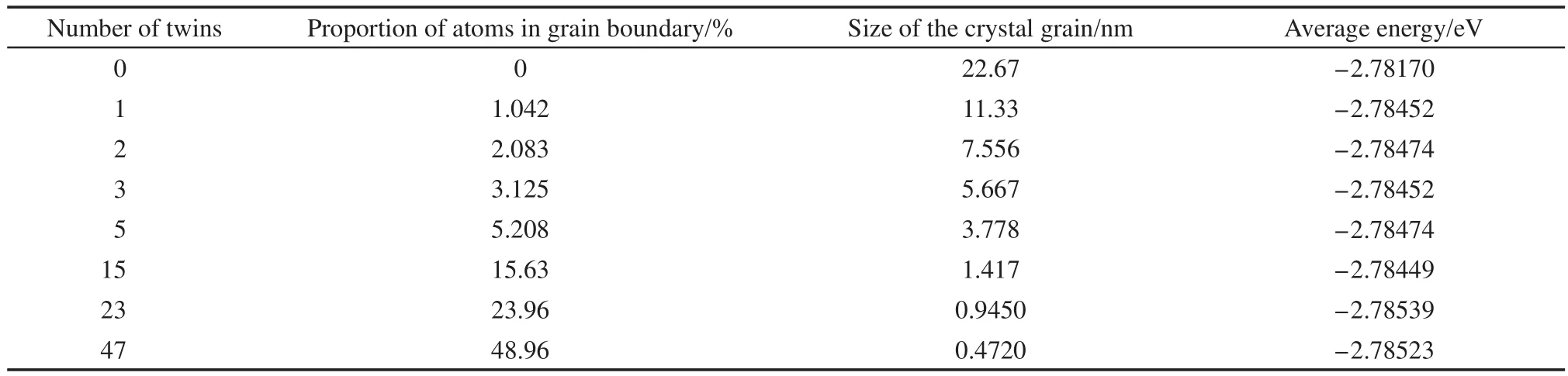
表1 不同孪晶界密度银纳米线的晶体学特点Table 1 Crystallographic characteristics of Ag nanowires under different twin boundary densities

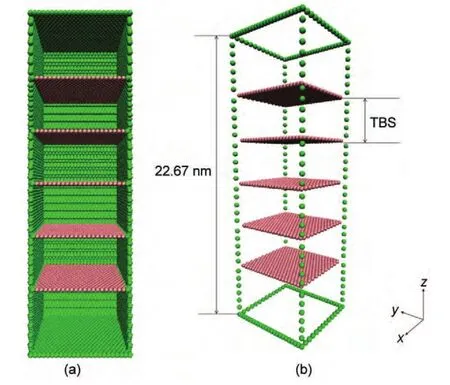
图1 五重孪晶银纳米线的初始构型图Fig.1 Undeformed configurations of Ag nanowire with five twins

在塑性形变区域内,纳米线在拉伸力下所产生的应变越大,延展性越好.由图4(b)可以看出,随着孪晶界间距的增大,纳米线的屈服应变近似线性地减小,孪晶越多纳米线的延展性越好.值得注意的是,单晶银纳米线的屈服应变仍然要大于含有一个孪晶界的纳米线.这说明孪晶界可以增强纳米线的延展性,从而起到强化纳米线的作用.

由图4(c)可看出,在拉伸载荷作用下,随着应变量的不断增大,所有纳米线的应力以相同的斜率线性增加,这表明银纳米线的杨氏模量受孪晶界的影响不显著,与Liu37和Zhang30等得出的结论相同.计算得到本文中[111]晶向的Ag纳米线的杨氏模量大小为(94.0±3.6)GPa,相对偏差为3.8%.虽然随着孪晶界间距的增大杨氏模量变化不明显,但是整体呈逐渐增加的趋势,单晶银纳米线的杨氏模量高于孪晶银纳米线,对这种现象比较合理的解释是,在拉伸力下孪晶界可以使纳米线的应变量减小,从而强化纳米线.

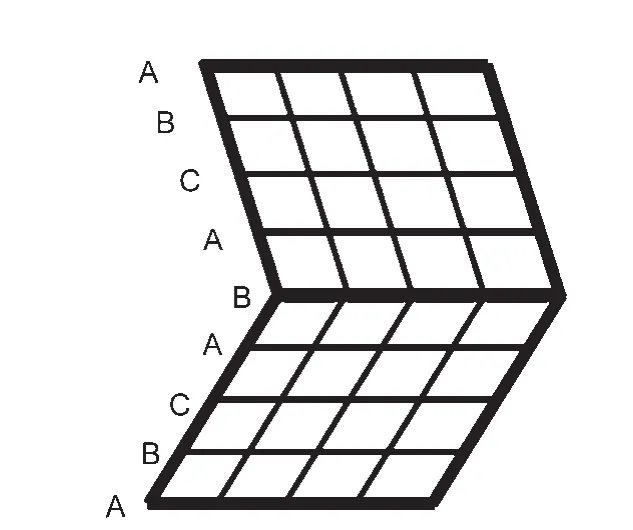
图2 孪晶机制示意图Fig.2 Schematic illustration of twinning mechanism

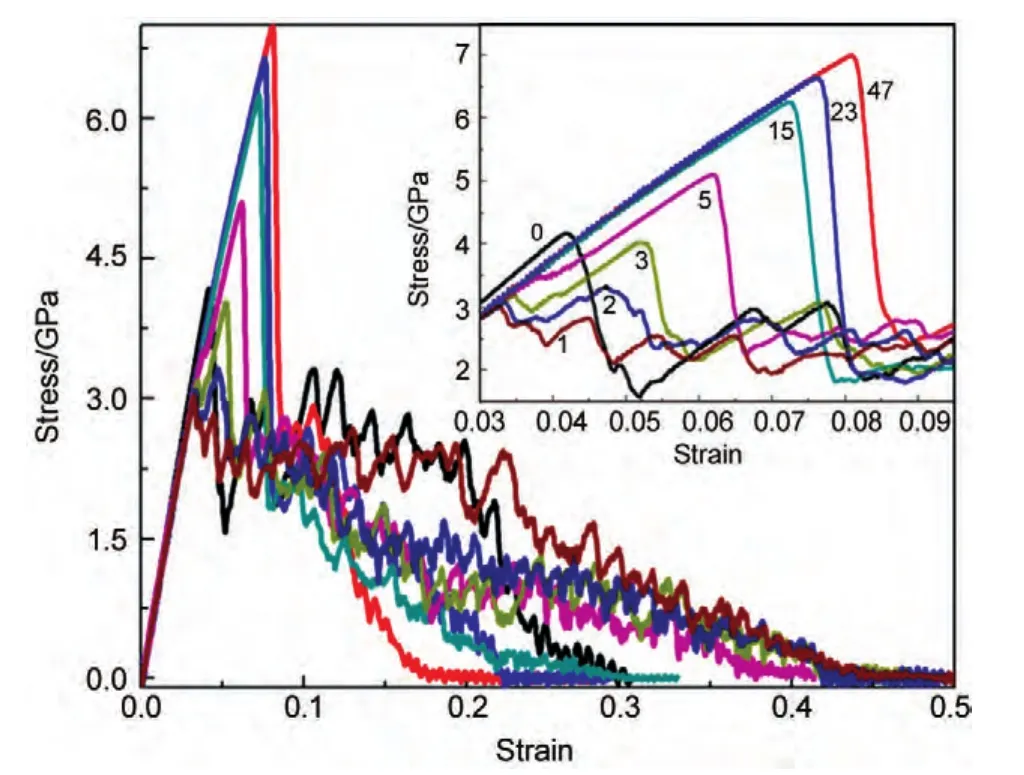
图3 不同孪晶界密度下8个模拟银纳米线拉伸的应力应变曲线Fig.3 Tensile stress-strain curves for the eight simulated Ag nanowires under different twin boundary densities during tensile deformation

另外,在塑性形变区域内,随着孪晶界间距增加,即孪晶界密度的减小,纳米线的断裂应变逐渐增大,如图4(d)所示.孪晶越多,纳米线的断裂应变越小,对这种现象比较合理的解释是,孪晶间距越大,在孪晶内部可以产生的位错滑移越多,相反孪晶间距较小,位错滑移受阻于孪晶界,孪晶内可以产生的位错滑移较少.这说明孪晶可以提高纳米线的强度.当晶粒的长径比大于1的时候,银纳米线的断裂应变小于单晶银纳米线.

由此可以得出,当孪晶界在五个以上时,孪晶银纳米线的强度要高于单晶银纳米线;当孪晶界个数小于三个时,单晶银纳米线的强度要高于有孪晶的纳米线.以上研究表明,孪晶界对纳米线并不一定起到强化作用,孪晶界是否可以强化纳米线还取决于晶粒长径比等因素,当晶粒在z方向上的尺寸显著小于x和y方向上的尺度时,孪晶界对纳米线起到强化作用.特别需要指出的是,我们的研究结果与以往报导的关于孪晶界强化作用的结果不同,以往的报导指出孪晶界对纳米线起到增强作用,42,43本文分析了孪晶界密度和晶粒长径比等因素对纳米线强度的综合影响,为构建高强度纳米线打下基础.

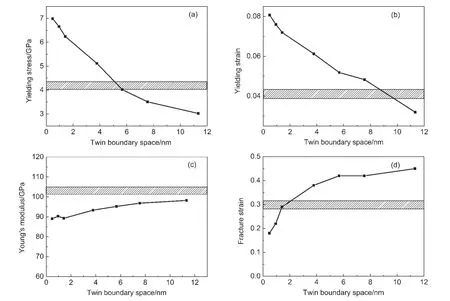
图4 不同孪晶距对银纳米线力学性质的影响Fig.4 Mechanical properties of Ag nanowires with different twin boundary spaces

我们做了不同孪晶界密度下银纳米线的径向分布函数,图5所示为单晶银纳米线与含有一个、五个和十五个孪晶界的银纳米线的径向分布函数(RDF),从下往上依次对应图中曲线,并且对应于各纳米线的屈服点处和断裂点处.图5(a)为纳米线在屈服点处的RDF图,将含有一个、五个和十五个孪晶界的纳米线相比较,RDF峰形变化不明显.孪晶纳米线和单晶纳米线均在0.70个晶格处出现最高峰即第一近邻峰,说明在10 K的模拟温度下原子的短程有序性较好.而对于单晶银纳米线,在1个晶格处的第二近邻峰的峰高相对于孪晶纳米线明显增加50%,说明孪晶纳米线在第二近邻处的有序性明显降低.第三近邻峰出现在1.22个晶格处(图5(a)),单晶的第三近邻峰劈裂出的一个小峰(1.26晶格),是单晶的特有峰.在1.40个晶格处出现的峰是第一近邻峰的倍频峰,其右侧又出现一个单晶的特有峰(1.44晶格).在1.57个晶格处出现第四近邻峰,单晶的第四近邻峰劈裂出的一个小峰(1.60晶格).2个晶格以上,峰比较密集,这说明原子排布依然保持了有序的状态.

图5(b)为纳米线在断裂点处的RDF图,孪晶纳米线的RDF峰仍保持一定的规律性,和屈服点处相比变化不大.单晶纳米线的RDF峰相比较屈服点处的RDF峰,其在1-2个晶格之间的两个特有峰左移至1.15和1.35个晶格处,且在1.60个晶格附近的特征峰消失,在1.90个晶格处的特征峰也向左移动.特征峰左移和消失的原因可能是拉伸过程中形成位错滑移,破坏了原子的有序性.2-3个晶格之间单晶峰高明显增加,说明单晶的远程有序性较好.

3.3 形变过程的微观结构分析

为了说明孪晶界对纳米线形变的主要作用机理,以及孪晶界密度对纳米线强度的影响,我们对含有二个、五个孪晶界的银纳米线和单晶银纳米线的拉伸变形过程进行了详细研究.在单晶银纳米线中,位错成核是由纳米线中部的表面原子上产生,如图6(a)中字母A所示.但位错滑移可以穿过整个纳米线,在端面的对面位置交叉混合.经过14.75 ps滑移面A由产生到发展到贯穿整个纳米线.

图5 含一个、五个和十五个孪晶界银纳米线与单晶银纳米线的径向分布函数Fig.5 Radial distribution function of Ag nanowires with one-twin,five-twin,and fifth-twin boundaries and single crystalAg nanowire

图7给出了含有二个孪晶界的银纳米线在拉伸变形中位错滑移的观察图,在拉伸载荷的作用下,首先在纳米线中部和上部三分之一处的表面原子边缘处对称产生位错成核,如图7(a)中字母A、B所示.滑移面与孪晶界呈60°角,位错滑移延伸并受阻于孪晶界.随着拉伸形变的增加,图7(d)中在纳米线上部晶粒中出现了新的滑移面C与最初的滑移面B相交,孪晶界阻挡了滑移面C的发展.随着拉伸进行,纳米线上部的晶粒开始收缩,直至断裂.这说明孪晶界可以阻碍位错的产生和发展,这与相关的实验44,45和计算模拟46研究结果一致.含两个孪晶界的纳米线晶粒长径比较大,位错滑移主要在纳米线的上部,纳米线最终在上部断裂.晶粒的长宽比较大,导致纳米线更容易断裂.

图6 单晶银纳米线在10 K的拉伸变形过程Fig.6 Instantaneous deformation processes of single crystalAg nanowires during tensile deformation at 10 K

图7 含二个孪晶界的银纳米线在10 K下的拉伸变形过程Fig.7 Continuous snapshots of initial yielding deformation of Ag nanowires with two-twin boundaries during tensile deformation at 10 K

图8 含五个孪晶界的银纳米线在10 K下的拉伸变形过程Fig.8 Continuous snapshots of initial yielding deformation of Ag nanowires with five-twin boundaries during tensile deformation at 10 K

图8给出了含有五个孪晶界的银纳米线在拉伸变形中位错滑移的观察图,在拉伸载荷作用下,对于[111]晶向的银纳米线,首先在孪晶界与表面原子边缘的交接处产生位错成核,47如图8(a)中字母A所示.随后产生的滑移面延伸至孪晶界被阻挡,不能继续延伸,滑移面与孪晶呈60°角.在拉伸载荷的继续作用下,纳米线中部的孪晶界作为位错源在其两侧产生位错,滑移面在其两侧多次反射,如图8(c)所示.在进一步拉伸变形作用下,如图8(d)所示滑移面由纳米线中部的孪晶界向两端相邻孪晶界扩散.纳米线中部开始收缩,应力集中在纳米线中部,导致中间处的滑移面增多,直至断裂.

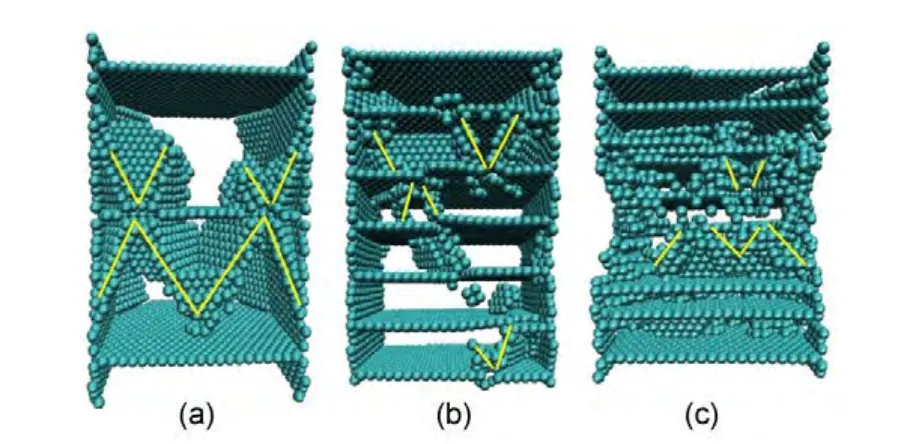
图9 含五个(a)、十五个(b)和二十三个(c)孪晶界的银纳米线产生滑移的截面图Fig.9 Cross-sectional views of Ag nanowires with fivetwin(a),fifteen-twin(b),and twenty-three-twin(c)boundaries

为了详细说明孪晶界对纳米线形变机理的影响,我们做了含有五个、十五个和二十三个孪晶界的银纳米线产生滑移的详细结构图,如图9所示,孪晶间距分别为3.778、1.417和0.945 nm,晶粒的长径比均小于1.由表面原子边缘产生的位错成核发展延伸到孪晶界被阻挡,使孪晶界表面变得粗糙不平,在进一步的拉伸作用下,从孪晶表面进一步滑移,这就使得孪晶界上发生位错滑移现象.孪晶界上形成的滑移面多次反射,晶粒长宽比小于一时均有此现象.滑移面由孪晶界向相邻孪晶界发展,48阻碍了位错的产生和滑移的发展,使纳米线得到强化.

3.4 拉伸形变机理与外部条件的关系

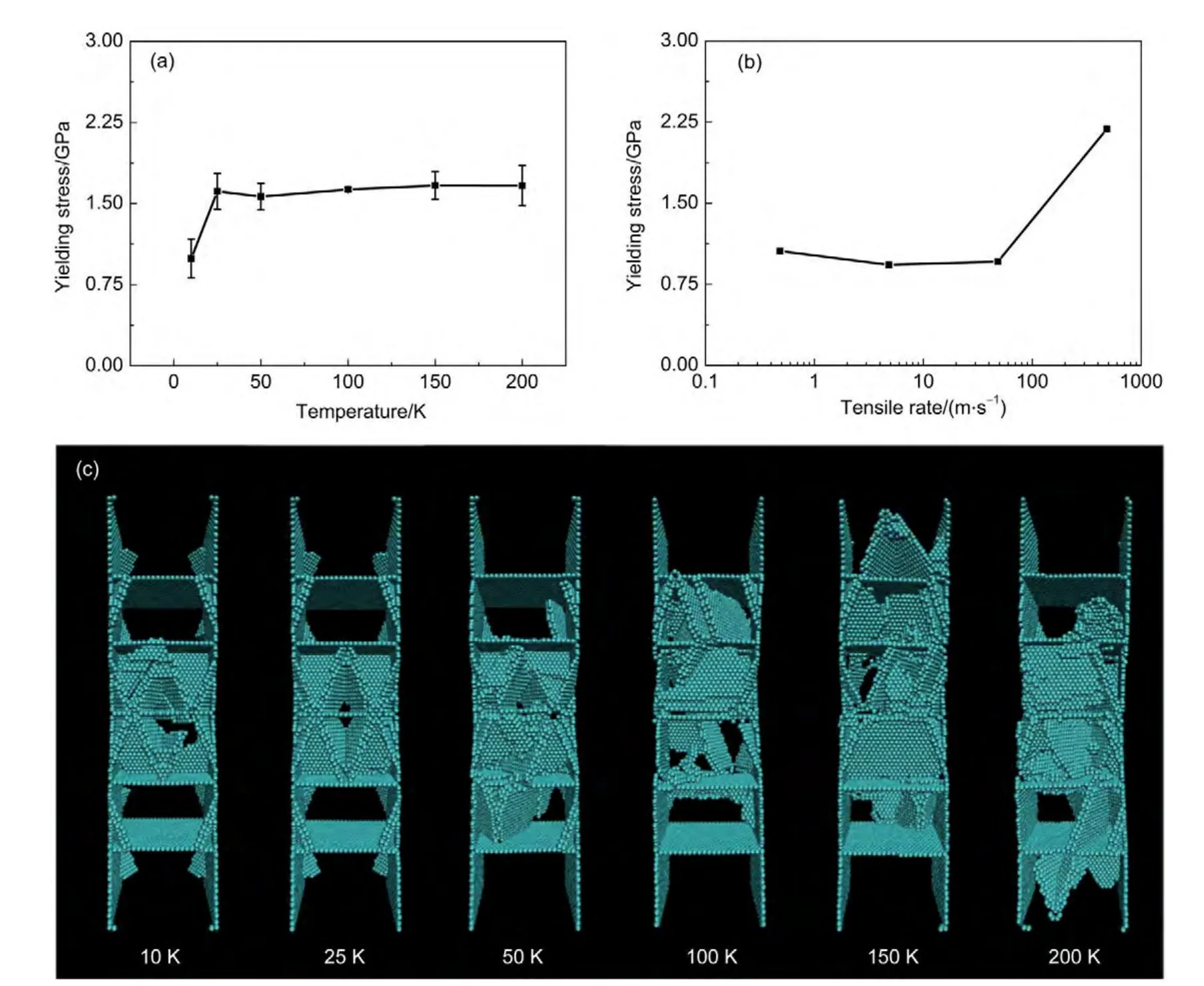
图10 含五个孪晶界样品的屈服应力差在(a)不同温度和(b)拉伸速度下的变化曲线;(c)含五个孪晶界的银纳米在不同温度下拉伸至300 ps时的原子结构图Fig.10 Yielding stress difference curves for the five-twin boundaries with(a)different temperatures and(b)different tensile rates;(c)continuous snapshots of the five-twin boundaries under uniaxial tensile loading of different temperatures at 300 ps

金属纳米线强度的影响因素很多,包括孪晶界、温度和拉伸速度等.特别需要指出我们的研究说明晶粒的长宽比小于1时孪晶界对纳米线起到强化作用,这种情况的出现可能与10 K的低温有关,关于温度对纳米线机械性质的影响已经被广泛报导.49,50而且,最近的实验研究表明孪晶对纳米线的影响很大程度上受到温度的影响,51温度越高,纳米线的屈服应力越低.

为了更好地说明孪晶结构对纳米线强度的影响,我们用分子动力学的方法,研究了不同温度和拉伸速度对孪晶银纳米线和单晶银纳米线屈服应力的影响,结果如图10所示,图10(a,b)纵坐标为含有五个孪晶界的银纳米线与单晶银纳米线的屈服应力之差.随着温度的增加,含有五个孪晶界的纳米线与单晶纳米线的屈服应力之差先增大然后趋于稳定,如图10(a)所示在10 K时最低,升高到25 K时趋于稳定.这说明超低温时孪晶增强作用不明显,温度大于25 K时孪晶的增强作用趋于稳定.图10(c)为在不同温度下对含五个孪晶银纳米线进行拉伸至300 ps时刻的原子结构图,图中可以看出在10 K超低温时,位错滑移相对于其他温度较少.可能是因为超低温时原子的运动幅度较小,拉伸不容易使原子偏离平衡位置,导致孪晶对纳米线强度的影响减小.

随着拉伸速度的增加,孪晶纳米线与单晶纳米线的屈服应力之差呈现先稳定再急剧增大的趋势,如图10(b)所示.随着拉伸速度的增大,拉伸冲击由准平衡态拉伸向高拉伸速度的非平衡态转变.拉力做功增大,导致原子动能分布的涨落加大,在准平衡态拉伸时,涨落幅度较小,孪晶对纳米线的增强作用对拉伸速度的依赖关系不明显.高速拉伸时,涨落幅度增大,能量富集区域会造成原子运动异常剧烈进而形成位错,原子的形变以无定形结构为主,其在晶粒内部的发展受到结构相对稳定的孪晶界阻塞,因而表现出较大的孪晶界对纳米线的增强作用.

4 结论

利用分子动力学的方法模拟了[111]晶向的孪晶银纳米线和单晶银纳米线的力学行为,从模拟结果得知,在弹性形变区域,银纳米线的杨氏模量受孪晶界的影响不明显.在塑性形变区域内,位错滑移优先从纳米线表面原子边缘上产生;孪晶界密度较小的孪晶纳米线其晶粒在z方向上的长度明显大于晶粒宽度,导致纳米线屈服应力比单晶纳米线还要小,并没有实现纳米线的强化;孪晶界密度较大时晶粒的长宽比小于1,孪晶界阻碍了位错滑移的产生,从而使得纳米线得到强化;在进一步的拉伸应力下,孪晶界也可以作为位错滑移的来源.这反映了孪晶界对纳米线拉伸形变影响并不只是起到加强作用,只有当孪晶界密度较大,晶粒长宽比小于1时,才能观察到纳米线强度的明显增加,要综合考虑孪晶界密度和晶粒尺寸对纳米线的综合影响,来更好地发展高强度的纳米线.

(1) Sun,W.;Zhang,J.J.;Zhao,J.W.Acta Phys.-Chim.Sin.2013,29,1931.[孙 玮,张晋江,赵健伟.物理化学学报,2013,29,1931.]doi:10.3866/PKU.WHXB201305311

(2) Branicio,P.S.;Rino,J.P.Phys.Rev.B2000,62,16950.doi:10.1103/PhysRevB.62.16950

(3) Ikeda,H.;Qi,Y.;Cagin,T.;Samwer,K.;Johnson,W.L.;Goddard,W.A.Phys.Rev.Lett.1999,82,2900.doi:10.1103/PhysRevLett.82.2900

(4) Christ,A.;Zentgraf,T.;Kuhl,J.;Tikhodeev,S.;Gippius,N.;Giessen,H.Phys.Rev.B2004,70,125113.doi:10.1103/PhysRevB.70.125113

(5) Gülseren,O.;Ercolessi,F.;Tosatti,E.Phys.Rev.B1995,51,7377.doi:10.1103/PhysRevB.51.7377

(6) Lai,S.;Guo,J.;Petrova,V.;Ramanath,G.;Allen,L.Phys.Rev.Lett.1996,77,99.doi:10.1103/PhysRevLett.77.99

(7)Alexandrov,A.S.;Kabanov,V.V.Phys.Rev.Lett.2005,95,076601.doi:10.1103/PhysRevLett.95.076601

(8) Zhao,J.W.;Wang,F.Y.;Jiang,L.Y.;Yin,X.;Liu,Y.H.Acta Phys.-Chim.Sin.2009,25,1835.[赵健伟,王奋英,蒋璐芸,尹 星,刘云红.物理化学学报,2009,25,1835.]doi:10.3866/PKU.WHXB20090909

(9)Tian,M.L.;Wang,J.U.;Kurtz,J.;Mallouk,T.E.;Chan,M.H.W.Nano.Lett.2003,3,919.doi:10.1021/nl034217d

(10)Wang,J.;Tian,M.;Mallouk,T.E.;Chan,M.H.J.Phys.Chem.B2004,108,841.doi:10.1021/jp035068q

(11) Lu,K.;Lu,L.;Suresh,S.Science2009,324,349.doi:10.1126/science.1159610

(12) Lu,L.;Sui,M.;Lu,K.Science2000,287,1463.doi:10.1126/science.287.5457.1463

(13) Lu,L.;Shen,Y.F.;Chen,X.H.;Qian,L.H.;Lu,K.Science2004,304,422.doi:10.1126/science.1092905

(14) Lu,L.;Chen,X.;Huang,X.;Lu,K.Science2009,323,607.doi:10.1126/science.1167641

(15)Zhong,S.;Koch,T.;Wang,M.;Scherer,T.;Walheim,S.;Hahn,H.;Schimmel,T.Small2009,5,2265.doi:10.1002/smll.v5:20

(16) Marszalek,P.E.;Greenleaf,W.J.;Li,H.;Oberhauser,A.F.;Fernandez,J.M.Proc.Natl.Acad.Sci.U.S.A.2000,97,6282.doi:10.1073/pnas.97.12.6282

(17) Wu,B.;Heidelberg,A.;Boland,J.J.Nat.Mater.2005,4,525.doi:10.1038/nmat1403

(18)Greer,J.R.;Oliver,W.C.;Nix,W.D.Acta Mater.2005,53,1821.doi:10.1016/j.actamat.2004.12.031

(19) Frøseth,A.;Van Swygenhoven,H.;Derlet,P.Acta Mater.2004,52,2259.doi:10.1016/j.actamat.2004.01.017

(20) Frøseth,A.;Derlet,P.;Van Swygenhoven,H.Appl.Phys.Lett.2004,85,5863.doi:10.1063/1.1835531

(21)Yang,Z.Y.;Lu,Z.X.;Zhao,Y.P.J.Appl.Phys.2009,106,023537.doi:10.1063/1.3186619

(22)Yang,Z.Y.;Lu,Z.X.;Zhao,Y.P.Comput.Mater.Sci.2009,46,142.doi:10.1016/j.commatsci.2009.02.015

(23) Frøseth,A.;Derlet,P.;Van Swygenhoven,H.Scripta.Mater.2006,54,477.

(24)Yamakov,V.;Wolf,D.;Phillpot,S.;Gleiter,H.Acta Mater.2003,51,4135.doi:10.1016/S1359-6454(03)00232-5

(25)Jin,Z.H.;Gumbsch,P.;Ma,E.;Albe,K.;Lu,K.;Hahn,H.;Gleiter,H.Scripta.Mater.2006,54,1163.doi:10.1016/j.scriptamat.2005.11.072

(26) Cao,A.;Wei,Y.Phys.Rev.B2006,74,214108.doi:10.1103/PhysRevB.74.214108

(27) Cao,A.;Wei,Y.J.Appl.Phys.2007,102,083511.doi:10.1063/1.2794884

(28)Afanasyev,K.A.;Sansoz,F.Nano Lett.2007,7,2056.doi:10.1021/nl070959l

(29) Zhang,Y.F.;Huang,H.C.Nanoscale Res.Lett.2009,4,34.doi:10.1007/s11671-008-9198-1

(30) Zhang,J.;Xu,F.;Yan,Y.;Sun,T.Chin.Sci.Bull.2013,58,684.doi:10.1007/s11434-012-5575-3

(31)Yuan,L.;Jing,P.;Liu,Y.H.;Xu,Z.H.;Shan,D.B.;Guo,B.Acta Phys.-Chim.Sin.2014,63,1.[袁 林,敬 鹏,刘艳华,徐振海,单德彬,郭 斌.物理化学学报,2014,63,1.]doi:10.3866/PKU.WHXB201311263

(32)Gao,Y.;Fu,Y.;Sun,W.Comput.Mater.Sci.2012,55,322.doi:10.1016/j.commatsci.2011.11.005

(33) Hoover,W.G.Phys.Rev.A1985,31,1695.doi:10.1103/PhysRevA.31.1695

(34) Nosé,S.J.Chem.Phys1984,81,511.doi:10.1063/1.447334

(35) Daw,M.S.;Baskes,M.I.Phys.Rev.Lett.1983,50,1285.doi:10.1103/PhysRevLett.50.1285

(36)Zhao,J.W.;Yin,X.;Liang,S.;Liu,Y.H.;Wang,D.X.;Deng,S.Y.;Hou,J.Chem.Res.Chin.Univ.2008,24,367.doi:10.1016/S1005-9040(08)60077-X

(37) Liu,Y.;Zhao,J.;Wang,F.Phys.Rev.B2009,80,115417.doi:10.1103/PhysRevB.80.115417

(38) Wang,D.;Zhao,J.;Hu,S.;Yin,X.;Liang,S.;Liu,Y.;Deng,S.Nano Lett.2007,7,1208.doi:10.1021/nl0629512

(39) Wang,F.;Gao,Y.;Zhu,T.;Zhao,J.Nanoscale Res.Lett.2011,6,1.

(40)Zhao,J.;Murakoshi,K.;Yin,X.;Kiguchi,M.;Guo,Y.;Wang,N.;Liang,S.;Liu,H.J.Phys.Chem.C2008,112,20088.doi:10.1021/jp8055448

(41)Wang,F.;Sun,W.;Wang,H.;Zhao,J.;Kiguchi,M.;Sun,C.J.Nanopart.Res.2012,14,1.

(42) Cao,A.;Wei,Y.;Mao,S.X.Appl.Phys.Lett.2007,90,151909.doi:10.1063/1.2721367

(43) Deng,C.;Sansoz,F.Phys.Rev.B2010,81,155430.doi:10.1103/PhysRevB.81.155430

(44) Wang,J.;Li,N.;Anderoglu,O.;Zhang,X.;Misra,A.;Huang,J.;Hirth,J.Acta Mater.2010,58,2262.doi:10.1016/j.actamat.2009.12.013

(45)Wang,Y.D.;Liu,W.;Lu,L.;Ren,Y.;Nie,Z.H.;Almer,J.;Cheng,S.;Shen,Y.F.;Zuo,L.;Liaw,P.K.Adv.Eng.Mater.2010,12,906.doi:10.1002/adem.201000123

(46) Li,X.;Wei,Y.;Lu,L.;Lu,K.;Gao,H.Nature2010,464,877.doi:10.1038/nature08929

(47) Deng,C.;Sansoz,F.Appl.Phys.Lett.2009,95,091914.doi:10.1063/1.3222936

(48) Wei,Y.Mater.Sci.Eng.A2011,528,1558.doi:10.1016/j.msea.2010.10.072

(49) Cao,A.;Ma,E.Acta Mater.2008,56,4816.doi:10.1016/j.actamat.2008.05.044

(50)Gao,Y.;Wang,H.;Zhao,J.;Sun,C.;Wang,F.Comput.Mater.Sci.2011,50,3032.doi:10.1016/j.commatsci.2011.05.023

(51) You,Z.;Lu,L.;Lu,K.Scripta.Mater.2010,62,415.doi:10.1016/j.scriptamat.2009.12.002