镁金属孪晶变形的实验和理论模型研究进展

甘元超

（中国工程物理研究院流体物理研究所，四川 绵阳 621999）

镁、钛等密排六方（Hexagonal close-packed，HCP）金属由于具有低密度、高比强度等优点，在航空航天、国防军事和生物医学等领域被广泛应用。这类HCP 金属作为防护结构材料时，其作用环境往往有高温、高压、高应变率、强冲击等特点。材料在这种极端条件下的变形和破坏是一个复杂的动态过程，宏观上表现为材料的形状、粒子速度和应力/应变等在短时间内发生剧烈变化，微观上则呈现出材料位错密度和织构不断变化以及产生孪晶成核、成长和退孪晶等变形机制[1]。纯镁及大部分镁合金的塑性变形机制有基面、柱面、锥面滑移和锥面孪生。在室温变形中，由于柱面和锥面滑移的临界分解剪应力（CRSS）远高于基面滑移而不易被启动，只有基面和柱面上3 个密排方向组成了2 个独立滑移系，提供垂直于c轴方向的应变，而平行于c轴方向的应变主要由锥面孪生产生，所以在HCP 金属中往往表现出较强的孪晶行为。伴随着孪晶的成核和成长，进一步促进了材料的塑性变形，并且孪晶有时也是材料的破坏源[2]。

相对于位错滑移，孪晶变形主要具有两个特点：一是孪晶变形具有极性，孪晶剪切变形只出现在一个方向上，相反方向并不发生变形，而滑移一般在两个方向都可以产生变形；二是孪晶变形会导致变形区域相对于未变形区域（一般以基体表示）成镜面对称关系，使得变形后孪晶区域的晶粒取向发生变化，这种变化可以使得变形前具有硬取向的晶粒向软取向转化，促进产生新的位错滑移以及变形孪晶，从而提升金属材料的塑性变形能力。激活镁金属位错滑移的CRSS 一般在1～100 MPa 范围内，但激活孪晶则需要更大的应力，所以初始时会产生一定的位错滑移变形，进而促进孪晶的产生，这在变形阶段较为常见。孪晶的形成过程一般可描述为孪晶成核、扩展和增长等：当外加载荷达到一定强度时，孪晶在晶界、位错和杂质等附近产生成核；在外力的持续作用下，孪晶沿着孪晶面向孪晶方向扩展，最终达到另一侧的晶界或位错等结构，阻碍孪晶的进一步扩展。部分学者指出，孪晶成核需要的应力较大，而孪晶扩展时所需的应力较小。同时在与孪晶面不平行的作用力下，孪晶会沿着垂直于孪晶面方向增长，使得孪晶的厚度增加，孪晶区域逐渐形成一个椭球，最终孪晶区域占据大半部分晶粒，晶粒的取向和晶界等发生变化，在孪晶区域进一步产生滑移和二次孪晶。当孪晶形成后，沿初始载荷相反的方向加载可能会产生退孪晶，使得孪晶区域缩小或者消失。由于退孪晶不需要孪晶成核，只是孪晶界面向孪晶区域移动，所以退孪晶所需的应力低于孪晶。退孪晶在工程材料加工中应用较多，许多学者研究发现，在镁合金中退孪晶行为往往会使材料的屈服强度下降，通过对材料进行退火或引入二次孪晶能够有效抑制退孪晶[2–4]。

影响孪晶变形行为的因素很多，如取向织构、晶粒尺寸、应变率、温度、晶格结构和应力状态等。在准静态和中低应变率（< 104s−1）下，可通过实验和理论模拟研究晶粒尺寸和取向织构等因素对于孪晶变形行为的影响，普遍认为晶粒增大在一定范围内对孪晶的增长起促进作用，而晶粒取向与孪晶成核有较为直接的关系。但在高应变率下，孪晶的成核和成长机理与准静态有所不同。同时在强冲击载荷下，温度和应变率更加难以控制，且变形历时很短（一般小于1 µs），物理量和微观结构变化剧烈，使得研究强冲击载荷下孪晶的变形行为较为困难。本文将简要介绍镁金属中孪晶变形机理的研究进展，评述晶粒取向、晶粒尺寸和应变率等因素对孪晶变形成核和成长影响的实验和理论模拟进展，最后展望相关实验方法和理论模型的应用。

1 镁金属孪晶变形实验研究

孪晶变形是晶粒内的局部变形，与材料的微结构特征密切相关，在影响孪晶激活和成长的因素中，科研人员对晶粒尺寸、取向织构和应变率等进行了大量研究。相关研究表明：晶粒取向与孪晶的成核有直接的关系；晶粒尺寸对孪晶的增殖和成长有较大的影响；而应变率的影响较为复杂，特别是在高应变率（> 105s−1）的冲击载荷下，受实验条件限制，对孪晶成核和成长过程的原位研究相对较少，更多是在实验后对样品进行回收表征，反推孪晶在材料变形过程中可能的机理。

1.1 取向织构对孪晶变形的影响

晶粒取向对孪晶成核有直接的影响，当作用在晶粒内的外部荷载一定时，晶粒取向的Schmid 因子（SF）决定了作用在孪晶面上的分解剪切应力（RSS）大小，当RSS 逐渐增长至大于或等于该孪晶的成核CRSS 时，孪晶发生成核，即孪晶的启动一般是通过与晶粒取向密切相关的Schmid 定律来判定的[5]。Park 等[6]进行了不同方向上的Mg-3Al-1Zn 镁合金准静态压缩实验，发现{1012}孪晶出现在基体中，{1012}-{1012}双孪晶和{1012}退孪晶出现在孪晶带中，通过电子背散射衍射（EBSD）和SF 分析发现，SF 和晶粒尺寸的耦合作用决定了孪晶的选择机制。Xu 等[7]在孪晶主导的变形中发现，对样品沿横向（TD）拉伸与沿挤压方向（ED）或TD 方向压缩产生的应力-应变曲线形状明显不同，在应变为拉伸时产生拉伸孪晶，压缩时则出现双孪晶。

图1 孪晶晶粒数与孪晶Schmid 因子的关系[8]Fig. 1 Relationship between twin grain number and twin Schmid factor[8]

但孪晶并不是必须发生在所有具有相同取向的晶粒内，Beyerlein 等[8]进行了纯镁在室温和准静态（10−3s−1）下的压缩实验，通过EBSD 研究了材料变形后的孪晶特征，分析了晶粒取向和晶体尺寸对孪晶成核和成长的影响，发现随着晶粒SF 的增大，孪晶发生率也随之上升，而在SF 较低的晶粒内，孪晶的成核几率降低，如图1 所示。他们进一步指出：在较宽SF 范围内晶粒均出现了孪晶变形，说明孪晶并不只出现在最容易产生孪晶的晶粒内（SF > 0.375）；SF 在0.375～0.5 区间时晶粒内同样存在非孪晶区域，说明孪晶并不只在最优取向的晶粒内成核，孪晶成核同时受其他因素的影响。一些研究也发现，孪晶不一定发生在SF 最大的晶粒内，有时会优先发生在能够实现应变兼容和最小塑性功的邻近晶粒内。Jonas 等[9]研究镁合金中的压缩孪晶时发现，当半数孪晶的SF 在0.3～0.5 范围内，而接近半数孪晶的SF 在0.15～0.30 范围内时，甚至5%孪晶的SF 在0.03～0.15 范围内，同样部分高SF 孪晶并未产生，这种产生低SF 孪晶的现象可解释为临近晶粒之间的应变兼容。如图2(a)所示，孪晶区域（红色边界）贯穿的晶粒拥有较硬的晶粒取向，容易产生孪晶，而临近晶粒的取向则不易产生孪晶，但由于孪晶在晶界上形成了应变梯度，致使较低SF 的晶粒中也产生孪晶。Mu 等[10]在镁合金中通过Taylor 模型指出，应变兼容与最小塑性功的原理是一致的，拥有最低SF（0.323）的孪晶变体仅需要较低能量即可被激活，而高SF 孪晶变体则需要较高的能量才能激活。

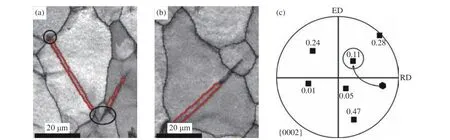
图2 (a)应变为0.08 时AM30 样品2 个压缩孪晶的EBSD 图（黑色圆圈表示应变兼容）；(b)临近轧制方向取向的晶粒内形成的{1011}压缩孪晶（红色）的EBSD 图；(c) 2(b)图中基体的(0002)极图（黑色六边形）、6 个孪晶取向（黑色正方形）和选择的临近晶粒孪晶取向（黑色圈内）以及它们的Schmid 因子[9]Fig. 2 (a) EBSD map of AM30 sample pulled to 0.08 strain showing two contraction twins (The black circles indicate strain compatibility.); (b) EBSD map of a {1011} contraction twin (in red) formed within a near rolling direction orientation;(c) (0002) pole figure for the Fig.2 (b) matrix (black hexagon), the six twin variants (black squares),the selected variant (circled in black), and their respective Schmid factors[9]

Barnett 等[11]在研究镁合金时发现，{1011}主孪晶与Schmid 定律吻合较好，而{1012}主孪晶相对于{1011}主孪晶与Schmid 定律偏离，但发生在{1011}孪晶区域内的{1012}二次孪晶并不符合Schmid 定律，这种非Schmid 行为发生的原因可能是{1012}二次孪晶发生在主孪晶形成的区域内必须为主孪晶和二次孪晶共面提供最小的应变兼容。Lou 等[12]进一步指出，这种晶粒之间的应变兼容使得局部应力发生波动，致使孪晶出现在偏离高SF 的区域。Song 等[13]通过晶体学分析发现，大多数晶粒内的孪晶选择与Schmid 定律是一致的，同时在晶界孪晶与孪晶的相互作用下，局部应变兼容也是一个重要因素。目前看来，SF 并不能作为判定孪晶启动的唯一因素，许多学者对Schmid 定律进行了修改，如采用修正Schmid 因子（MSF）[14–15]、有效Schmid 因子（ESF）[16]、广义Schmid 因子（GSF）[17]和组合Schmid因子（CSF）[18]等。Guo 等[19]通过SF 和应变兼容因子联合分析{1012}孪晶的成核机理，{1012}孪晶对出现在SF 和应变兼容较大的临近晶粒内的可能性更大，这种孪晶对可以穿越多个晶粒，在超过3 个晶粒后形成孪晶链。Liu 等[20]从滑移对晶界的冲击进而刺激孪晶产生出发，同样引入了一个描述滑移和孪晶的几何兼容因子，发现晶界处的应变转移在孪晶成核中起到了重要作用。Shi 等[21]也表示，低SF 孪晶 的形成需考虑临近晶粒内的变形机制，受到多种不同变形机制（包括高CRSS）的共同调节作用。

1.2 晶粒尺寸对孪晶变形的影响

研究发现，在一些金属中，随着晶粒尺寸的增大，孪晶的体积分数也会增加[22]。晶界处的应力集中对孪晶成核有促进作用，晶粒的增大使得晶界面积增大，从而影响孪晶的成核密度；另一方面，晶粒的大小也会限制孪晶的成长，较小晶粒内生成的孪晶也较小。Kim 等[23–24]在预压缩的镁合金中发现，粗晶粒内{1012}孪晶比细晶粒内更多，这是由于孪晶应力降低和孪晶SF 增加的共同作用，同时粗晶粒内拥有更大的孪晶体积分数、更剧烈的织构和更少的孪晶边界。Dobroň等[25]采用声发射技术对AZ31 镁合金在压缩下的孪晶变形进行研究，结合EBSD 确定{1012}孪晶更加偏好于大晶粒，但随着塑性变形的进行，{1012}孪晶同样也会在较小晶粒内产生。Beyerlein 等[8]和Ghaderi 等[26]指出，随着晶粒面积改变，镁中的孪晶数量有所变化，但孪晶厚度变化不大，这或许说明晶粒尺寸对镁中的孪晶成核影响较大而对孪晶成长影响较小，并且发现只有那些存在孪晶的晶粒会呈现出孪晶随着晶粒面积增大而增大的特点。Kumar 等[27]进一步比较了镁、钛和锆的孪晶变形特点，发现拉伸孪晶（Tensile twin，TT）和压缩孪晶（Compression twin，CT）的数量和厚度随着晶粒面积的变化发生了不同程度的变化。如图3 所示，在晶粒尺寸较小时，孪晶的成核几率随着晶粒尺寸的增大而增加，当晶粒尺寸达到一定值时成核孪晶达到饱和状态。镁的拉伸孪晶厚度和数量与晶粒尺寸关系不大，而钛和锆的拉伸孪晶分别在孪晶厚度和孪晶数量上均呈明显增长。Asgari 等[28]采用霍普金森压杆（SHPB）对晶粒尺寸为6、18 和37 µm 的镁合金在应变率为1 100 s−1的冲击载荷下进行了动态力学研究，发现相同冲击载荷下较粗晶粒的孪晶体积分数更大且应变硬化率更高，而细晶粒则表现出更好的强度和延展性，增大晶粒尺寸后的孪晶中同时观测到了双孪晶和压缩孪晶的激活和形成。

图3 晶粒内孪晶数量和厚度随晶粒面积的变化[27]Fig. 3 Evolution of the number and thickness of twins with grain area[27]

金属材料的屈服强度和流动应力与晶粒尺寸之间的关系一般是基于Hall-Petch 等式，该等式可以简单描述为应力与晶粒直径平方根的倒数成线性关系。Hall-Petch 等式一般适用于以孪晶为主导变形的材料中[5,29]，但与位错滑移相比，孪晶主导的Hall-Petch 关系的斜率更大些[30]，同时也表明孪晶应力对晶粒尺寸更敏感。Marcinkowski 等[31]将这种斜率更大现象的原因解释为非最优孪晶取向和较高孪晶成核应力的联合，Armstrong 等[32]则强调孪晶伴随着局部微塑性导致应力集中，而滑移导致的变形更加均匀统一。Hong 等[33]进一步将孪晶界对应力的促进解释为孪晶诱导晶粒尺寸变小，通过Hall-Petch关系使得晶粒内应力增加。Bohlen 等[34]进行了镁合金挤压研究，发现在沿着ED 方向压缩下{1012}孪晶的Hall-Petch 斜率是沿着ED 方向拉伸下位错滑移的1.58 倍。Yu 等[35–36]也对镁合金的Hall-Petch 斜率进行了综合性研究，其中取向织构、晶粒尺寸和温度对斜率都有重要的影响，同样这些因素对孪晶变形的影响也较大，或许是通过孪晶为主的变形机制实现对斜率的作用。Somekawa 等[37]研究了固溶体对镁合金孪晶Hall-Petch 的影响，发现Hall-Petch 中初始应力 σ0的增长顺序为：Mg–Y > Mg–Zn > Mg，说明固溶体具有强化效应，而合金元素对Hall-Petch 斜率的影响并不是很大。在进一步的实验中发现，影响Hall-Petch 斜率最大的因素并不是SF，而是晶界的特征。对于非均匀晶粒材料，Hall-Petch 关系可能并不适用，Jin 等[38]针对具有双峰晶粒的镁合金，发现在细晶粒中屈服强度由位错滑移控制，而粗晶粒中由孪晶主导。他们对Hall-Petch 关系进行了修改，统计晶粒尺寸的百分比，通过晶粒尺寸的体积分数对不同阶段的硬化曲线进行叠加计算，获得不同晶粒尺度下的应力-应变曲线，如图4 所示。

图4 双峰晶粒AZ91 合金的晶粒尺寸分布(a)和应力-应变曲线(b)[38]Fig. 4 Grain size distribution (a) and stress-strain curves of bimodal-grained AZ91 sample (b)[38]

1.3 应变率对孪晶变形的影响

孪晶在高应变率下的成核和成长与低应变率下明显不同。随着应变率不断提高，孪晶的成核率也不断上升，使得孪晶体积分数不断增加，此时一些SF 较低的晶粒内也会产生孪晶，在晶界和孪晶交叉处产生的应力集中也可能成为孪晶潜在的成核源[12,39]。Wang 等[40]指出，在准静态下孪晶更容易成长。Dudamell 等[41]也发现，在AZ31 镁合金中应变率会大幅提升{1012}拉伸孪晶的激活率，但对压缩孪晶和二次孪晶影响不大。Maksoud 等[42]通过实验发现，AZ31 镁合金的应变率敏感性在高应变率下变为非线性。Li 等[43]在AZ31 镁合金的SHPB 实验中发现，镁合金的屈服强度相对于准静态下增长了55%。虽然沿ED 方向压缩时都发生了由于拉伸孪晶激活导致的晶格旋转，但在进一步的EBSD 分析中，当应变为16%时，高应变率下二次压缩孪晶的体积分数更高些。Ahmad 等[44]也在AZ31B 镁合金中发现，3 500 s−1应变率下TD 和RD 方向的破坏应变相比于准静态下分别提高了30%和55%，同时在RD 方向上的变形孪晶起到了重要的作用，所以在高应变率下AZ31 镁合金的孪晶变形增大，进而提高了材料的屈服强度和承载能力。

Mao 等[45]在AZ31B 镁合金的高应变率（约106s−1）研究中发现了一种反常现象，随着变形的进行，在单个基体内产生了不同的{1012}孪晶变体，其中一种孪晶变体可以完全被另一种包围，形成孤立的区域，这种反常的孪晶之间的相互作用并不能采用传统的孪晶理论来解释，本文采用一种非孪晶位错理论进行分析，如图5 所示。

图5 (a)基于传统孪晶理论的孪晶相互作用（由于孪晶位错不能穿透孪晶界，当两者相互靠近时将阻碍孪晶的增长）；(b)非位错形式的孪晶增长（T1）（孪晶能够通过改变孪晶面产生分支而包围另一个孪晶）；(c) 非位错形式的孪晶增长（T2）（孪晶通过侧向成长而绕过另一个孪晶）[45]Fig. 5 (a) Twin-twin interaction based on classical twinning theory (The growth of the twin variants will be impeded as the variants approach close to each other because the twinning dislocations are unable to penetrate the twin boundaries.); (b) non-dislocation mediated twin growth (T1) (A twin variant can branch out by changing the habit plane and surround the other variant.); (c) nondislocation mediated twin growth (T2) (A twin variant can spread laterally and grow around the other variant.)[45]

相对于拉伸孪晶，压缩孪晶和双孪晶等由于拥有较高的CRSS，并不容易被激活。Berge 等[46]在0.1 s−1应变率下AZ31 镁合金中发现了压缩孪晶和双孪晶，而准静态10−3s−1下未发现两种孪晶。Wang 等[47]在AZ91 镁合金的平板冲击实验（应变率约为105s−1）中发现，除了较常见的{1012}拉伸孪晶，{1011}压缩孪晶和{1011}-{1012}双孪晶同样存在。随着冲击速度的提高，所有孪晶的数量都显著增加，而拉伸孪晶在尺寸和数量上都占据主导作用。但Dixit 等[48]在应变率103s−1下的纯镁压缩实验中并未观察到压缩孪晶的存在。Yu 等[49]采用分离式霍普金森拉杆（SHTB）对EW75 镁合金进行的动态拉伸实验中，只发现了{1012}拉伸孪晶，提高应变率并没有对{1012}拉伸孪晶的数量产生太大的影响，这与AZ31 镁合金的动态实验差别较大，而且还发现AZ31 的中的{1012}拉伸孪晶在变形早期就开始发展[50–51]，随着应变率提高，也极大地提高了{1012}拉伸孪晶的激活率。Yu 等[49]对此进行了解释：首先，EW75 镁合金的弱取向更加偏向于基面滑移的启动；其次，EW75 镁合金中稀有元素的添加可能增大了{1012}拉伸孪晶的激活应力；最后，柱面和锥面滑移的CRSS 随着变形过程温度的升高而降低。

在平面撞击等更高应变率的变形中也能观察到孪晶的产生，同时材料有时会发生弹性前驱波衰减，而在那些孪晶变形较少的材料中，前驱波衰减并不明显[52–53]，这可能是孪晶导致的缺陷数量不同引起的。如图6(b)所示，实线箭头指明了一般拉伸孪晶作用于冲击波的过程，冲击波作用后的拉伸孪晶导致该处的部分晶格发生旋转，当从后表面反射回来的稀疏波作用时往往会产生退孪晶，虚线箭头指明了形成的退孪晶致使孪晶区域部分晶格退回至原来的取向[1,54]。Kanel 等[55]对镁单晶的c轴、a轴和沿c轴45°方向进行了冲击加载。实验结果显示：c轴的雨贡纽弹性极限（HEL）最大，45°方向最小；沿c轴压缩的回收样品中发现了大量孪晶，随着冲击波传播至样品内部，孪晶逐渐减少。同时在所有实验中都发现了弹性前驱衰减，作者指出这是位错和孪晶共同作用的结果。在层裂强度研究中，相比于铝和铜等立方金属，镁单晶的层裂强度比多晶更高，这可能是由于变形孪晶减小了单晶的均质性，孪晶的边界可以作为破坏的成核源。Dixit 等[53]也进一步证实了弹性前驱衰减与孪晶变形有关。Rességuier 等[56]对单晶镁进行更高应变率的激光加载，同样发现材料的层裂行为与孪晶有着密切的关系，包括初始存在的和冲击产生的孪晶，并且裂纹沿着特定的孪晶方向扩展。除了前驱波和卸载阶段，剪切强度[57]、强烈的Bauschinger 效应[2]和应力凸起[55]也都与孪晶变形紧密相关。

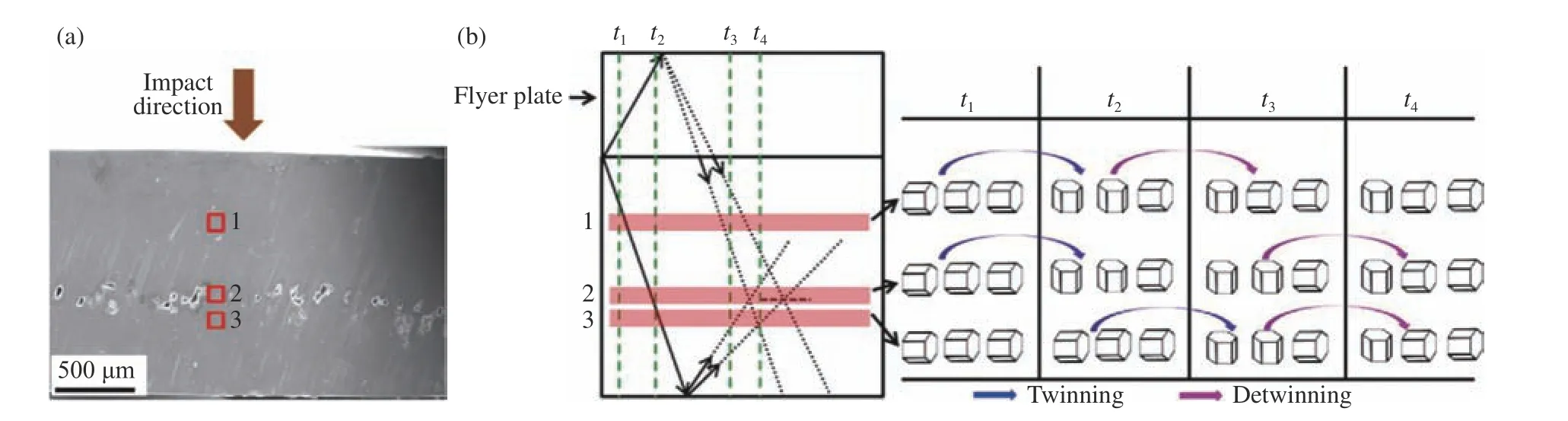
图6 冲击波传播和材料微结构：(a)冲击示意图和3 个观测点；(b)冲击波传播的时间-位置图和3 个观测点在不同时刻（t）的微结构[1]Fig. 6 The propagation of shock wave and the microstructure of material: (a) The schematic diagram of shock and three observation point; (b) the time-distance diagram of the shock experiment and corresponding schematic diagrams of the microstructure at 3 location at different times (t)[1]

在材料变形的影响中，温度软化和应变率硬化被认为有相似的效应，许多学者也将温度和应变率对孪晶变形的影响综合起来研究[58–59]；相对于取向织构和晶粒尺寸等因素，晶界和应力状态的不断变化使得研究材料变形过程中这两种因素对孪晶的影响变得复杂且困难，直接针对晶界和应力对孪晶成核和成长的相关研究较少，目前较多的研究指出孪晶起源于晶界且更加偏好于小角度晶界，这也基本符合小角度晶界处的应变兼容和应力集中等条件[9]。

2 镁金属孪晶变形理论模型

由于孪晶变形处于微介观尺度，对孪晶变形的理论和模型研究体现了多尺度方法的运用，较常见的有晶体塑性理论[60–61]、位错动力学[62]、分子动力学[63]和相场[64]等，相关方法对研究孪晶变形的侧重点不同。晶体塑性理论是在介观尺度发展起来的方法，通过建立位错滑移和孪晶变形与宏观连续介质之间的联系实现对材料宏观变形的模拟预测，除了可以与实验宏观结果进行比较，还可以获得位错、滑移和孪晶等微观机理的演变信息，研究变形机制对材料屈服、硬化和破坏的影响，同时对于单晶和多晶材料晶粒的取向织构改变也能随时追踪。位错动力学方法更多侧重于位错对孪晶和孪晶界的作用和相互关系，进而影响材料的塑性变形和相变等。分子动力学方法也具有类似的理论体系，但由于现有计算能力的限制，后两种方法一般只能研究较小尺度范围内的变形，并不能对宏观变形真实模拟。目前，在研究和建立孪晶模型的框架中，更多的是基于晶体塑性理论。本节主要针对晶体塑性模型框架下的孪晶理论模型进展进行评述。

晶体塑性理论是从材料的微介观尺度变形（位错滑移、孪晶和相变等）角度研究材料的弹塑性变形行为。Taylor[65]最早做出晶体塑性理论的开创性工作，随后Hill[66]以及Asaro 等[67]进一步对晶体塑性理论进行了完整的阐述。在Taylor 模型体系中，单个晶粒内所有单晶的应变是相等的，晶粒的应力则由单晶应力通过体积分数叠加获得，这种假设保证了晶界处应变协同条件，而应力则存在梯度。另一种相似的模型是Sachs 模型[68]，与Taylor 模型采用应力应变相反的假定，但现有研究中更多采用Taylor 模型。自洽模型也是一种应用较广的模型，模型将所有晶粒考虑为包含在一个无限均匀等效的介质中，通过Eshelby 夹杂理论和自洽条件使得模型满足应力平衡。Lebensohn 等[69–70]基于自洽模型建立了黏塑性自洽模型（VPSC），该模型在材料大变形、不同变形条件下力学行为和织构演化等方面应用广泛。详细的晶体塑性模型介绍参考文献[71–73]。

在只有滑移的变形理论体系中引入孪晶需要考虑两方面内容：（1）晶粒内变形不再是均匀的，孪晶区域和基体的应变不同，在晶粒内呈现应变梯度；（2）除基体以外，孪晶区域有特定的取向，使得在计算过程中孪晶和基体的取向数量增加，给计算造成了困难。最早考虑晶格重新定向的孪晶模型是由Vanhoutte[74]提出的，后续学者在此基础上开展了大量工作，常见的孪晶模型有主孪晶重新定向（PTR）、体积分数转变（VFT）和全拉格朗日方法等。在PTR 模型中，追踪每个晶粒内孪晶区域的体积分数增长情况，采用一种统计的判定模型，当达到判定条件时，整个晶粒旋转至主孪晶的取向，但并不增加晶格的取向数量，在每个时间步结束时，每个晶粒的最终取向要么被滑移转动要么采用孪晶的取向[74]。PTR 模型的缺点是只关注最主要的孪晶体系，PTR 模型更适用于只有一种孪晶的材料变形，而对于具有多种孪晶且其对塑性变形的贡献相差不大的情况，PTR 模型的计算误差较大。所以，在PTR 模型中将主滑移、二次滑移和主孪晶作为塑性变形机制。VFT 模型是由Tomé等[75]提出的，采用加权晶粒取向描述追踪由孪晶产生的大量新取向，通过引入取向的欧拉角，由滑移引起的旋转将体积分数转入临近的单元内，而孪晶引起的选择则转入非临近的单元，这样在准确追踪孪晶体积分数的同时避免了增加初始的取向数。在VFT 模型中考虑更多的同样是主滑移、二次滑移和主孪晶。

PTR 模型和VFT 模型存在一个缺点，即两种模型会将孪晶区域识别成全新的晶粒，在该晶粒内可以像未发生孪晶的基体那样产生新的滑移和孪晶，而孪晶区域与基体的变形特征明显不同，全拉格朗日方法克服了上述缺点。1998 年，Kalidindi[60]在原来只有滑移的晶体塑性本构模型中引入了孪晶变形，如图7 所示，在该模型中将晶体的变形过程分为两部分：晶体从初始构型到中间构型发生了塑性变形，包含位错滑移和孪晶变形；从中间构型到最终构型是弹性变形，发生了晶格畸变和扭转。模型中滑移和孪晶的剪切应变率和宏观速度梯度张量通过孪晶体积分数叠加起来，建立了宏微观之间的联系，相关表达式为

图7 包含孪晶的变形梯度F 分解示意图[60]Fig. 7 Extension of the multiplicative decomposition of the deformation gradient F to include deformation twinning[60]

需要注意的是，只有当孪晶的RSS 为正时才会产生孪晶，这体现了孪晶的变形具有方向性。基于Kalidindi 孪晶模型框架，国内外众多学者展开了分析研究工作[77–78]。Liu 等[79]在晶体塑性模型中考虑了温度对滑移和孪晶的影响，同时提出了一种自下而上的计算方法，通过代表性体积单元（RVE）预测了镁多晶的力学响应和孪晶、织构的演化。Izadbakhsh 等[61]对模型的变形机制进行扩展，并考虑了滑移、主拉伸孪晶、主压缩孪晶和二次拉伸孪晶，采用不同的硬化演变函数追踪基体、主孪晶和二次孪晶区域内的织构演化，获得了与实验吻合的结果。Zhang 等[80]对孪晶和滑移的硬化进行了研究，针对不同孪晶采用不同的硬化模型，考虑了孪晶与孪晶、滑移与孪晶的相关作用，对镁单晶和多晶在不同载荷方向上的变形进行模拟预测，预测了镁单晶中由于孪晶饱和产生的晶格旋转，旋转之后的变形机制能够表征材料后续的塑性硬化，如图8 所示。Ardeljan 等[81]对滑移和孪晶阻力的演化一方面采用应变、温度和应变率函数的位错密度硬化形式，同时通过另一种显示方法将孪晶层嵌入到有限元多晶模型中，实现了对孪晶变形的直观描述。Sun 等[82]在类似孪晶的思想中引入了相变机制，对铜单晶沿[541]方向单轴拉伸下的应力-应变曲线上由相变引起的拐点进行预测，但并未很好地区分模型中的变形机制。还有一些研究[83–84]也对晶体塑性理论下的孪晶变形进行了深入的探讨和广泛的应用。

图8 单晶镁平面应变压缩模拟（实线）和实验（A～G）的应力-应变曲线比较[80]Fig. 8 Comparison of stress–strain responses from single crystal Mg plane-strain compression simulations(solid lines) with experiments (A–G)[80]

为了预测孪晶和退孪晶的变形机理，Proust 等[3]对CG 模型中材料再加载变形过程进行更改，提高其他孪晶体系的CRSS，使得孪晶区域中与原来相同的主孪晶体系被激活，这时并不考虑为二次孪晶而是孪晶向基体转变，这个过程可以使整个孪晶区域转变为初始晶粒。Proust 等的退孪晶模型过于简单，Wang 等[4,91]建立了物理基础的孪晶-退孪晶模型（TDT），该模型包含4 种变形机制：孪晶成核、孪晶成长、孪晶收缩和重孪晶。如图9 所示，孪晶成核和成长也就是孪晶的变形过程，孪晶收缩和重孪晶则是退孪晶过程。整个晶粒被分为基体和孪晶区域，初始时晶粒内没有孪晶，当基体应力达到一定值时孪晶开始成核；随着应力的持续增大，孪晶继续成核，将孪晶成核看成基体减少和孪晶传播两方面，它们的驱动力则由各自区域内的应力控制；而当退孪晶的RSS 超过孪晶收缩的CRSS 时，孪晶开始收缩，也可分解为基体扩展和孪晶减少；重孪晶则是在孪晶区域内形成新的孪晶。在CG 和TDT 模型中都把孪晶当成一个新的区域，只是在TDT 模型中所有孪晶都可以形成，而在CG 模型中只考虑了主孪晶。通过对孪晶形成时晶粒的分解，忽略孪晶成核和重孪晶较小的体积分数，考虑孪晶成长和收缩时孪晶体积分数的变化率，则有

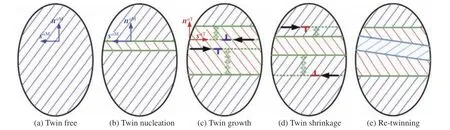
图9 晶粒内的孪晶和退孪晶过程示意图（绿色实线为孪晶界，蓝色和红色点线代表晶格取向；sαM 和nαM分别表示基体中孪晶面和法线， sαT 和 nαT表示孪晶区域中孪晶面和法线方向）[91]Fig. 9 Schematic representation of twinning and de-twinning in a grain (Solid green lines represent twinning boundaries; Lattices orientations are represented by dotted blue lines and dotted red lines; sαM and nαM are the twinning plane and normal direction in matrix; sαT and nαT are the twinning plane and normal direction in twin domain.)[91]

Wu 等[92]建立了TNPG 孪晶模型，将孪晶过程分为孪晶成核、孪晶增殖和孪晶成长。孪晶成核需要较大的应力，而在孪晶从一侧晶界增殖到另一侧晶界过程中需要的应力则逐渐降低，在孪晶增殖和孪晶成长交接时应力达到最小值，而后孪晶成长，应力增大。采用一个固定的孪晶体积分数判定孪晶从增殖到成长的临界点，在孪晶增殖过程的硬化采用线性关系，孪晶成长过程则采用Voce 硬化，具体表达式为

图10 (a)孪晶不全位错通过孪晶面滑动和垂直于孪晶面增长到临近点X 的传播示意图（lglide和lgrowth为孪晶成核点到增长点X 的水平和垂直距离，vprop和vgrowth为孪晶沿孪晶面和孪晶面法线的增长速度）；(b)包含孪晶的多晶微结构（晶粒内不同颜色代表不同取向）[95]Fig. 10 (a) Sketch map of a twin partial dislocation propagation to a neighboring point X by respectively gliding on the twin plane and growing normal to it (lglide and lgrowth are the horizontal and vertical distances from twin nucleation point to growth point X. vprop and vgrowth are the growth velocity of twins along the twin plane and its normal.); (b) polycrystalline microstructure with twins (Different colors in grains represent different orientations.)[95]

上述孪晶模型大多用于准静态或者SHPB 冲击的应变率（小于104s−1）下，较多的是从孪晶的成核和成长等方面对孪晶进行描述，通过孪晶形成的剪切应变和体积分数研究孪晶对材料塑性变形的贡献，但现有的孪晶模型更多的是唯象和统计型，对影响具体孪晶因素的考虑尚有所欠缺，需开发考虑因素更为完善、适用性更强的孪晶模型。在更高的平板冲击应变率（大于105s−1）下孪晶模型的相关研究则较少，Winey 等[96]在各向异性材料模型中嵌入位错动力学、变形孪晶和剪切破坏来描述材料的非弹性变形，对于孪晶的考虑相对于Kalidindi 模型则更加简单，孪晶体积分数采用一种唯象模型，相关的成长率是孪晶RSS 和阻力的一次函数。在对铍单晶沿a轴的冲击模拟中该模型获得了表现出比只有滑移的模型更好的结果，在多波结构中与实验的趋势更加吻合，相关的变形机制激活率也证明了孪晶在后续变形阶段具有重要作用。Winey 等[54]和Renganathan 等[97]进一步采用了该模型对镁单晶的冲击变形进行模拟，证实了孪晶在速度剖面卸载阶段的重要作用，在不同的冲击方向下材料的速度剖面存在一定差异，分析指出这是滑移和孪晶变形机制竞争的结果。相对于中低应变率的孪晶模型，高应变率下孪晶模型除了考虑应变率的不同影响外，更加注重由于体积压缩和塑性功引起的温升对孪晶的影响。Feng 等[98–99]分别针对SHPB 和平板冲击，基于Kalidindi 模型建立起了包含滑移、孪晶和相变的本构体系，在孪晶模型中，孪晶的贡献来源于两方面：基体成长为孪晶的非负部分和孪晶到相变的非正部分，在硬化中仔细追踪基体和孪晶区域内的滑移对孪晶的作用，通过引入初始剪切应力参数考虑孪晶过程中的热耗散，保证孪晶模型的热动力学守恒。Feng 等[99]对单晶钛的c轴冲击进行了预测，模拟结果同样存在与实验一致的弹性前驱衰减等，并进一步指出这是孪晶的起始点，而在接近平台时的双波结构与相变相关联。

除了上述晶体塑性理论下较为常规的孪晶模型，将相场和晶体塑性模型结合起来研究孪晶变形也越来越受到更多的重视[100–102]。Kondo 等[100]在晶体塑性理论框架中融入相场模型，对镁单晶的孪晶和退孪晶变形进行预测分析，通过对孪晶相体积分数准确地计算，比经典模型更好地表征了孪晶与基体的边界和孪晶区域的局部剪切，同时通过有限元分析得出孪晶成核会降低材料的机械能。Liu 等[101]采用相场模型研究了镁金属拉伸孪晶的成核、扩展和成长，分析了孪晶扩展时的局部应力和应变状态，发现在孪晶尖端处存在应力集中，并进一步指出孪晶在晶界转移过程中局部应变兼容对于常规的SF 起着更大作用。Liu 等[102]同样在晶体塑性模型中融入了相场模型，通过相场模型准确区分出基体和孪晶区域的边界以及孪晶界迁移过程，在相场模型中引入实验测量的孪晶界面能和临界梯度判定从而对孪晶界宽度进行限定，实现了对孪晶形态学上孪晶成长的较好预测，相关研究对孪晶成核、成长和形态学研究具有重要意义。

3 总结与展望

本文对镁金属内孪晶变形的研究进展进行了评述，分别从实验研究和孪晶理论模型两方面进行追踪，在实验方面大量学者对影响孪晶激活和成长过程的因素进行了研究，其中取向织构、晶粒尺寸和应变率具有较大的影响。

取向织构决定了作用在晶粒内孪晶面的作用力大小，对孪晶的激活和成长有直接影响，普遍采用Schmid 定律来描述孪晶的激活，但越来越多的研究证明孪晶并不都发生在具有高SF 的晶粒内，晶粒与晶粒之间的取向差过大会导致在晶界处形成应力集中，为了满足晶界附近处的应变兼容条件，部分软取向形成的孪晶将穿透晶界至硬取向的晶粒中。这时Schmid 定律并不能作为判定孪晶启动的唯一条件，部分学者对Schmid 定律进行一定的修改，如加入应变兼容因子和几何兼容因子。

晶粒尺寸对镁金属拉伸孪晶和压缩孪晶有不同形式的影响，较为常见的是增大晶粒尺寸能拉伸{1012}孪晶的激活率，对拉伸孪晶的成长则影响不大。同样可以采用Hall-Petch 关系描述晶粒尺寸的影响，相对于位错滑移，孪晶主导的Hall-Petch 关系的斜率会更大一些，而在晶粒尺寸跨度较大的晶体中，可以采用晶粒尺寸百分比对Hall-Petch 关系进行修改，进而描述不同晶粒尺寸对材料硬化的影响。

应变率对孪晶的成核和增长都有较大影响，一般来说随着应变率的增大，孪晶的成核和密度都会增加，镁合金内的{1012}拉伸孪晶则相比于{1011}压缩孪晶对应变率更加敏感，但在不同镁合金中存在一定的差异，这可能是由于夹杂的其他元素对孪晶的激活应力产生影响，相关研究有待实验的进一步确定。在平板冲击的高应变率下，孪晶与弹性前驱波衰减、卸载和破坏等都存在密切联系。

目前，对镁金属孪晶变形的实验研究更多是基于实验前后的微观表征，研究实验前不同的微结构对材料力学性能的影响更多地局限于宏观性能表现方面，由于实验后的微观表征只能描述最后时刻的材料形貌，更甚者是材料经过热冷却和应力释放后的结果，对材料变形过程中的微观变形机制演变的描述并不准确，缺乏相关因素影响对孪晶变形过程的原位表征，该方向是国内外热门领域，具有较大的发展前景。在材料变形过程中，特别是动态加载下，存在相关因素的耦合，需要通过相关实验设计实现对部分因素的解耦。相对于霍普金森杆等中低应变率下镁金属的孪晶变形，在更高应变率的平板冲击下，相关因素对孪晶的影响研究较少，在高应变率下孪晶具有不同的表现形式，对材料的响应作用更加明显，相关因素的影响或许更加不可忽略。

孪晶的理论模型经历了一定发展过程，目前国内外采用的常见孪晶模型有：主导孪晶系旋转模型（PTR）、体积分数转换模型（VFT）、全拉格朗日方法、CG 模型、孪晶与退孪晶模型（TDT）和孪晶成核、增殖和成长模型（TNPG）等。在目前的孪晶模型中，更多地局限于考虑单一或部分因素，对应的理论模型一般针对特定变形条件下的特殊变形机理，这对孪晶模型在不同变形条件下的适用性提出了挑战。同时目前的孪晶模型更多的是基于唯象结构框架，对孪晶变形采取统计的形式进行描述，传统孪晶模型缺乏一定的物理基础，对孪晶的成核、扩展和成长等更多采用较简单的公式进行描述，而更低尺度上的位错动力学、分子动力学和相场等方法在研究孪晶形态学上的成核和成长、孪晶界对材料塑性作用和孪晶与滑移之间的相互作用等方面具有一定的优势，考虑加强不同尺度方法之间的联系，在完善的理论框架中融合不同尺度模型对从物理机理上研究材料宏观性能具有重要意义；现有的孪晶模型虽然考虑了一定的应变率效应，但对于高应变率下的平板冲击情况是否适用还有待验证，目前缺乏复杂高应变率下的动态孪晶模型，更高应变率下材料变形更加剧烈，材料的温度、晶粒尺寸和取向等都会发生相较于中低应变率下更大的变化，这些因素之间的相互耦合也对动态孪晶模型的建立提出了挑战；目前孪晶模型的研究更多局限于对材料塑性的影响，而对材料破坏影响的研究则较少，相关研究具有较大难度，但也是材料研究中不可避开的一个方面，整体模型的实现有待建立孪晶模型结果与破坏模型输入之间的联系。