冲击载荷下金属材料的微结构-加载特性-层裂响应关系概述
蔡 洋,李 超,卢 磊
(1. 顶峰多尺度科学研究所,四川 成都 610027;2. 西南交通大学材料科学与工程学院,四川 成都 610031)
冲击载荷下金属材料的变形损伤既是长期悬而未决的基础科学难题,也是工程应用的核心问题之一。发展基于物理的、有预测能力的变形损伤模型对预测工程装置的服役表现至关重要,而已有变形损伤预测程序过多依赖于经验和基于平均场的唯象模型。
大量实验表明,材料的变形损伤涉及多个时空尺度,微介观结构对材料在动态极端条件下的响应可能起到决定性作用。传统基于平均场的唯象模型的变形损伤模拟程序已无法满足工程实际需求,将微介观结构纳入变形损伤预测模型已成为研究热点之一。此外,变形损伤涉及缺陷的萌生及发展,是一个典型的势垒控制的动力学问题,因而具有很强的时间和率依赖性,亦反映在对加载特征的依赖性上,如热力学路径、应变率、脉冲宽度和幅度、外加物理场等。
层裂强度作为冲击变形损伤实验中重要的物理量,受到国内外学者的广泛关注[1–6]。例如,Johnson 等[7]研究了不同的脉冲宽度和应变率对无氧铜层裂强度的影响,并指出脉冲宽度和应变率对层裂强度的影响较小。相反,Chen 等[5]通过冲击实验发现铝的层裂强度随着应变率的增加而增加。此外,Butcher 等[8]通过调整脉冲持续时间,发现平板冲击下层裂不是瞬态发生的,而是与载荷历史相关。事实上,影响层裂强度的因素较多且相互耦合,而有关层裂强度的研究大多只涉及单一或少量的因素,且不考虑微介观结构的影响,致使研究结果千差万别。因此,本工作综述微介观结构和加载特征对金属材料变形损伤的影响,建立高应变率下金属材料的微结构-加载特性-层裂响应关系,为建立考虑加载特征和微介观结构效应的金属变形损伤模型奠定实验基础。
1 层裂实验
轻气炮是国内外广泛应用的实验室冲击加载装置,具有高速发射子弹的能力,可对固体材料产生108~1011Ρa 的冲击波压力,是研究动态高压下材料的状态方程、变形与损伤的有效工具[3,5]。图1 为轻气炮装置示意图[9]。轻气炮发射飞片撞击样品形成冲击波,样品在冲击波作用下发生变形,运用激光速度干涉技术测量样品的自由面粒子速度历史可获得雨贡纽弹性极限、层裂强度、拉伸应变率等物理量。
图2 为冲击加载下样品发生层裂时的波系传播x-t图及相应的自由面粒子速度(ufs-t)曲线。飞片和样品中的冲击波S 抵达各自的自由面后发生反射并形成卸载波R,飞片和样品中的两簇卸载波相向而行,两簇卸载波在样品的中间区域相互作用后使样品承受拉应力,当拉应力幅值超出材料的强度时,层裂发生。样品内部的变形损伤可以通过自由面的粒子速度推断,层裂发生后,源自样品自由面的卸载波在层裂面处发生反射成为拉伸波并传向样品自由面。样品自由面的粒子速度在t3时刻降至极小值,随后在压缩波的作用下逐渐升高。根据样品自由面速度曲线中的回跳速度[10–11]可以计算样品的层裂强度 σsp和动态拉伸过程(t2~t3)的拉伸应变率ε˙

式中: ρ0为样品的初始密度,CL为样品的纵波声速,CB为体积声速,ufs,2和ufs,3分别为t2和t3时刻样品自由面的粒子速度。

图 1 轻气炮加载装置示意图[8]Fig. 1 Schematic setup for gas-gun experiment[8]

图 2 层裂原理示意图[8]Fig. 2 Schematic illustration of spallation[8]
2 微介观结构
通常情况下,金属材料是由大量的晶粒组成的多晶体,金属材料的力学和物理性能通常与晶粒尺寸有关[12]。冷热加工和塑性成型过程中,金属材料中晶粒发生择优取向而形成的织构亦影响金属材料的性能。此外,晶界作为多晶金属中重要的面缺陷,畸变能较高,对多晶金属的塑性变形、强度和断裂等性能有重要的影响。类似地,多相合金中的相界面和元素偏析带也一定程度上影响材料的性能。为此,本节围绕晶粒尺寸、织构、晶界、相界和元素偏析带对冲击载荷下金属材料变形损伤的影响依次展开讨论。
2.1 晶粒尺寸
金属结构材料通常为多晶材料,材料的晶粒越细,强度和韧性越高,强度与晶粒尺寸的关系可以通过Hall-Ρetch 公式描述,细晶强化是源于晶界对位错滑移的阻碍作用[12–13]。然而,Hall-Ρetch 公式不一定适用于层裂强度的尺寸效应。一些研究发现,细晶铝和铜等金属的层裂强度低于粗晶材料[14–18];而另一些研究则发现相反的规律,超细晶铝、铜、钽和铁等金属[19–22]的层裂强度明显高于粗晶材料。此外,Escobedo 等[18]发现多晶铜的层裂强度随着晶粒尺寸从30~200 µm 增加有先降低后增加的趋势。这方面的分子动力学模拟受限于纳米晶粒尺寸范围,Schwartz 等[23]发现纳米晶铜的层裂强度低于单晶,Mackenchery 等[24]、Dongare 等[25]揭示了纳米晶铜的层裂强度随着晶粒尺寸(5~30 nm)的增加而下降。类似地,Yuan 等[26]模拟了纳米孪晶铜的层裂损伤,发现层裂强度随孪晶界间距(0.5~4.0 nm)的增加而下降。
针对上述晶粒尺寸对层裂强度影响的差异,Wilkerson 等[27]进行了系统的阐述(见图3):晶粒尺寸在毫米以上时,损伤以晶内成核为主,层裂强度与晶粒尺寸无关;当晶粒尺寸介于毫米和微米之间时,随着晶粒尺寸的降低,损伤模式由穿晶损伤转变为沿晶损伤,层裂强度随之降低;而当晶粒尺寸在微米以下时,层裂由沿晶损伤主导,高密度的晶界抑制损伤的长大,层裂强度随着晶粒尺寸的降低而增加。这一理论与Cheng 等[14]研究的多晶钽的层裂实验结果相符,大晶粒样品中穿晶孔洞数量比小晶粒样品中多(见图4),且晶内孔洞到最近晶界的距离大多集中在1/4 晶粒尺寸以内。
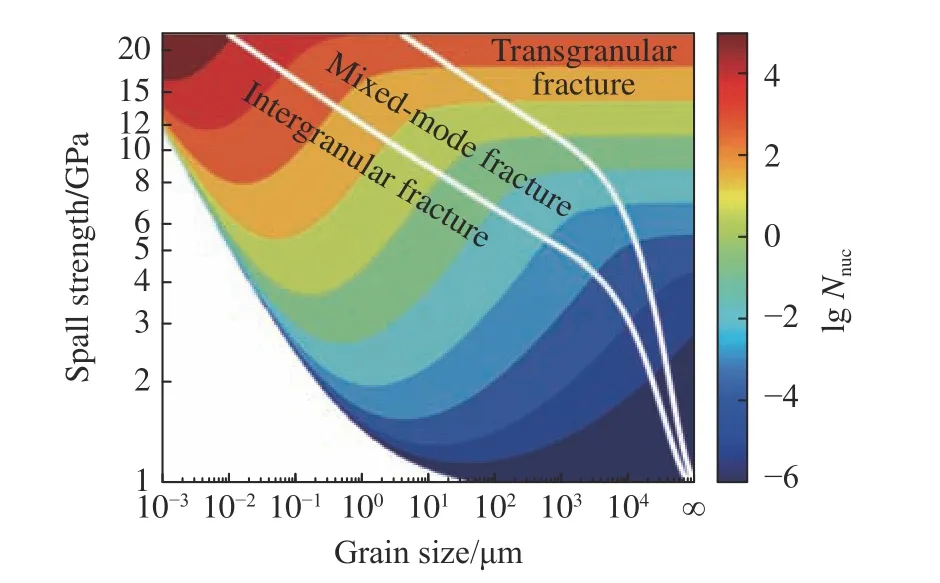
图 3 层裂强度及空隙密度与晶粒尺寸的关系[27]Fig. 3 Contour map demonstrating the grain size dependence of spall strength as a function of void density[27]

图 4 金属钽层裂损伤的微结构表征[14]Fig. 4 Microstructure characterization of spallation damage for tantalum[14]
另外,Trivedi 等[3]发现晶粒尺寸对层裂强度的影响与冲击压力有关:在21 GΡa 的冲击压力下,纯铝和铝合金的层裂强度随着晶粒尺寸的增加而明显增加;而在4 GΡa 的压力下,层裂强度基本不受晶粒尺寸的影响。这种差异可能是由于冲击压力较低时,层裂在拉应力脉冲平台处形成,层裂强度为拉应力平台的幅值,受微结构的影响较小[28]。因此,层裂强度的晶粒尺寸效应一方面与晶粒尺寸范围有关,另一方面又取决于加载特征。
2.2 晶体取向与织构
晶体的一个显著特征是具有各向异性,单晶材料表现为取向效应,多晶材料则在塑性成形或再结晶过程中出现一定的取向择优,即织构。在准静态加载下,织构对材料强度的影响与单晶取向类似,材料的弹性各向异性和塑性各向异性导致力学性能的各向异性[13]。对于FCC(面心立方)单晶,如单晶铝、铜、镍等,材料强度与施密特因子/泰勒因子成反/正相关,沿着[100]压缩,屈服强度最低;沿着[111]加载,屈服强度最高[29]。然而,在冲击载荷下,单晶层裂强度的各向异性在不同材料中存在不一致的结论。在FCC 单晶金属材料的层裂实验中:[100]单晶铜的层裂强度最高,[111]最低[17,30–31];而[111]单晶铝的层裂强度最高,[100]最低[5,32]。此外,Luo 等[4]通过分子动力学模拟发现,[111]单晶铜的层裂强度最高,[114]最低。Lin 等[33]采用分子动力学模拟发现[111]单晶铜的层裂强度比[100]低。模拟与实验之间的差异可能与冲击压力有关。同样,不同BCC(体心立方)单晶材料的层裂强度在实验和模拟研究中也有不同的各向异性[34–36]。单晶金属中没有晶界,层裂前因压缩和拉伸塑性导致的缺陷成为损伤的成核源,塑性的各向异性导致损伤异质成核的各向异性[34–35]。随着冲击压力的增加,冲击压缩阶段塑性变形随之增大,影响后续的层裂过程,致使层裂强度的各向异性出现差异。
多晶金属材料的织构通常也会造成层裂强度的各向异性。一些学者发现,铝合金沿纵向加载时的层裂强度高于沿横向加载[37]。钛、锆、钽、HY-100 钢和304 不锈钢等[38–40]的层裂强度受织构的影响较小,但织构对回跳速度斜率的影响较大,即影响层裂损伤的演化过程。Tan 等[39]发现对于具有强织构的轧制钛合金,沿轧面法向(ND)加载时的层裂强度略低于沿轧面横向(TD)加载。在初始层裂实验中,对于沿法向加载的钛合金,层裂处的裂纹通常垂直于冲击方向,然而对于沿横向加载的样品,层裂处的裂纹则呈现锯齿状且裂纹分布更离散。针对具有强丝织构镁合金,Dai 等[41]沿平行c轴及垂直c轴方向进行了平板撞击实验,结果同样表明:织构影响层裂断口的形貌特征;垂直c轴加载时,裂纹通常分布在样品中部,并且互相连通;平行c轴加载时,层裂处裂纹平行于RD-TD 面分布,且沿冲击方向较为离散。Yu 等[42]通过对热轧镁合金进行多次等通道转角挤压(ECAΡ)来改变其织构。虽然织构的改变对材料的层裂强度没有影响,但改变了层裂的产生方式。原始材料中层裂主要由沿晶界出现的微孔洞合并产生,改变织构后层裂则主要由内韧窝导致的微孔洞合并造成。Li 等[43]发现不锈钢的层裂强度在低压下显示出明显的各向异性(见图5),而在更高的压力下,则呈现出较弱的各向异性,这是由于随着冲击压力的升高,层裂损伤特征由解理裂纹转变为孔洞长大,表明多晶金属中层裂强度的各向异性亦受冲击压力的影响。与单晶中层裂强度各向异性的原因有所不同,多晶具有较多的缺陷,如晶界、相界、杂质颗粒等[38,44–46],它们都可以作为材料损伤的成核源,因而损伤成核受到各向异性塑性变形的影响较小;损伤演化的各向异性,如孔洞或裂纹容易沿着晶界面、相界面、滑移面或解理面等[38,43,45]长大,造成层裂强度的各向异性。而在较高的冲击压力下,材料内部呈现静水拉应力状态,损伤初期以孔洞的形式演化,导致各向异性材料的层裂强度呈现各向同性[43,47]。
材料层裂强度的各向异性与材料在准静态加载下断裂强度的各向异性差异较大,并且在不同材料中、不同冲击压力下,有不同的各向异性,其变化规律极其复杂,原因有3 方面:(1)材料的静态强度只与塑性成核有关,而层裂强度对应损伤的成核和长大,往往需要多个滑移系上的位错相互作用;(2)在层裂损伤前,材料经过冲击压缩和拉伸导致的塑性,具有不同的各向异性;(3)损伤演化也有各向异性,且受应力状态的影响。

图 5 不锈钢的自由面速度历史曲线[43]Fig. 5 Representative free surface velocity histories for stainless steel[43]
2.3 晶界类型
多晶金属中晶界作为最常见的缺陷,通常是层裂损伤的成核源,也对损伤演化有抑制作用[2,48]。层裂损伤的成核率一方面与晶界密度(或晶粒尺寸)有关,另一方面与晶界类型相关。Escobedo 等[49]发现金属Cu 中大角度晶界(> 50°)限制滑移传递,出现更大的应变不匹配,因而比 Σ3 晶界更容易损伤。Wayne 等[50]、Brown 等[51]通过对层裂试样进行回收表征,采用统计的方法研究了多晶铜中晶界取向差对层裂损伤的影响,发现损伤倾向于在中角度晶界(30°~40°)上成核,多晶钽中层裂形成的穿晶孔洞也有类似的晶界效应[14]。Fensin 等[52–53]采用分子动力学模拟方法探究了冲击加载下铜中规则和不规则 Σ11 晶界对层裂的影响,结果发现二者产生的塑性变形量使层裂强度出现12%的差别。该工作表明,晶界结构的微小差异会导致冲击响应中不可忽略的差别。晶界类型对层裂损伤的影响机制也较复杂,一般来说由于晶界两侧应力不尽相同,应力状态也会比较复杂,另外,晶界本身存在能量差异,有些会优先成核,但总体来说,高能量晶界比低能量角度更易于成核。
2.4 相 界

图 6 镁合金层裂损伤的X 射线计算机断层图像[41]Fig. 6 X-ray computed tomography images of spallation damage for the magnesium alloy[41]
在合金中,溶剂元素与基体元素形成固溶体或多相合金。根据第二相颗粒尺寸,两相合金可以分为弥散型和聚合型。对于弥散型两相合金,当第二相以细小弥散的微粒均匀分布于基体相中时,将一定程度阻碍位错运动,进而产生显著的强化作用,这种强化作用称为第二相强化[13]。然而,在冲击载荷下复相合金中的第二相颗粒或相界往往容易成为损伤的成核源,影响金属材料的层裂强度[54–59]。Tan 等[39]沿着轧面法向和横向对双相钛合金进行冲击加载,在相界处均发现了较多的微裂纹和孔洞,表明相界作为弱区有利于损伤形核,且不受加载方向的影响。Dai 等[41]运用同步辐射计算机断层扫描技术研究了镁合金沿不同方向加载时的层裂损伤特征(受合金制备工艺影响,镁合金中的第二相平行于轧面分布),结果表明:当沿着轧制方向(RD)冲击时,孔洞的分布较集中,且处于样品的中间位置,而沿着轧面法向冲击时,孔洞和裂纹呈孤立分布(图6),这一结果证明了相界对层裂有重要的影响,且第二相的各向异性分布直接影响层裂损伤特征。Chen 等[60–61]用分子动力学模拟了Ta 颗粒/纳米晶Cu 基体中的层裂现象,发现层裂强度随着Ta 含量的增加先增加后下降。这是因为Ta 的含量较少时,可以固溶在基体中抑制位错的产生,从而使孔洞成核也较困难;随着Ta 含量的进一步增加,Ta 元素形成第二相颗粒,作为损伤成核点,导致层裂强度下降。
对于聚合型两相合金,第二相尺寸接近基体尺寸。有些材料,相界通常作为层裂损伤的成核点,如双相不锈钢[43];而其他一些材料,损伤成核往往偏向于某一种相颗粒内部晶粒或晶界处,如Cu-Nb 合金中的Cu[62]、双相钛合金中的α相[63]、双相钢中的马氏体相[64]。作者认为损伤都是在高阻抗相颗粒内部成核,原因是当冲击波由高阻抗材料向低阻抗材料传播时,冲击波卸载后会在高阻抗材料中产生拉应力,导致损伤在高阻抗相内形核。
2.5 元素偏析带
合金中各组成元素在结晶时会出现元素分布不均匀的现象,杂质元素有时会聚集在界面附近,有时呈带状分散在晶粒中,为元素偏析带[65]。304 不锈钢轧制后,微观组织中普遍存在一种带状组织——合金元素偏析带。目前,元素偏析带对304 不锈钢在准静态下的力学性能影响较小。Ma 等[40]开展了冲击加载下304 不锈钢的层裂实验,发现元素偏析带对损伤特征和层裂强度有显著的影响,其原因在于元素偏析带及其与基体之间的界面是薄弱区域,损伤易在这些位置形核。此外,通过统计层裂面的损伤度发现,当加载方向与带状组织垂直时(图7 中Type Ⅱ),裂纹沿着层裂面扩展并联合形成大裂纹,表现出相对较小的损伤度,层裂强度随冲击压力的增加而增加(见图8);而当冲击方向平行于元素偏析带时(图7 中Type Ⅰ),将形成大量平行于元素偏析带的裂纹,且裂纹间的联合较少,表现出较大的损伤度,层裂强度基本保持不变(见图8,其中ara为回跳速度斜率)。这说明元素偏析带在晶粒中作为弱区,有利于损伤的成核与扩展,其作用类似于界面。

图 7 304 不锈钢中的元素偏析带以及层裂损伤特征[40]Fig. 7 Element segregation bands and damage features of 304 stainless steel[40]

图 8 304 不锈钢层裂强度与冲击压力的关系[40]Fig. 8 Spall strength of 304 stainless steel as a function of peak stress[40]
3 加载特征
层裂是由压缩冲击波在自由面反射的稀疏应力波相互作用形成的拉应力引起的,拉应力脉冲的参数直接影响层裂行为,而拉应力历史通常不能用实验的方法直接获得。图9 为冲击加载下样品不同截面处的应力历史,与压应力脉冲类似,拉应力脉冲形状大致呈梯形,分为上升沿、脉冲平台和下降沿[66–67]。拉应力脉冲的幅值和时长(脉冲时间)与压应力脉冲的幅值和时长呈正相关,且拉伸应变率正比于拉应力脉冲的上升沿斜率。因此,层裂实验中通常用应变率、压缩波的峰值应力和脉冲持续时间描述拉应力脉冲。本节围绕脉冲宽度、应变率和峰值应力对层裂强度的影响依次展开讨论。
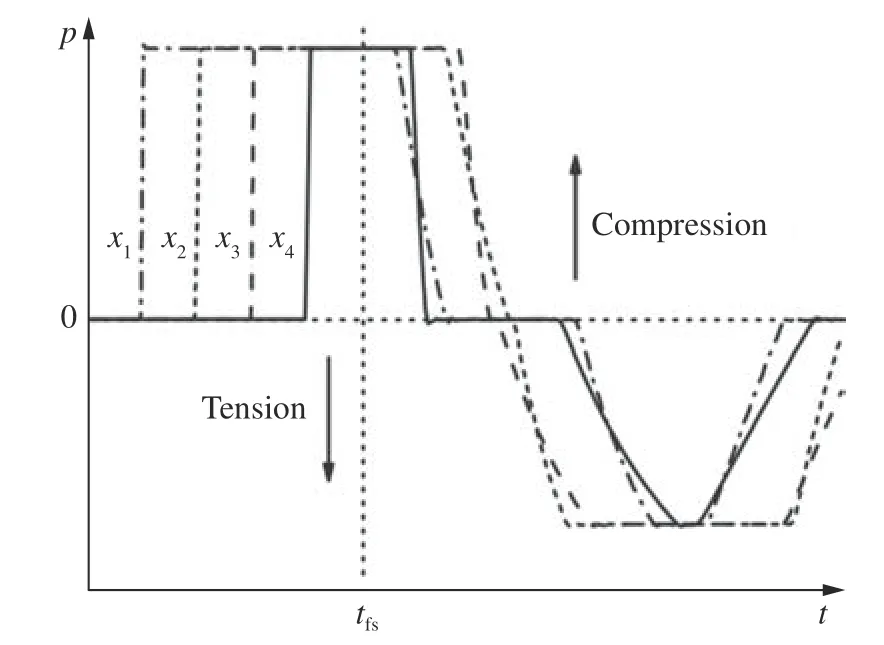
图 9 冲击加载下样品不同截面处的应力历史[66]Fig. 9 Stress histories in different cross-sections of a sample under shock loading[66]
3.1 加载波形
冲击加载是持续一段时间的脉冲加载,加载波形通常对变形和损伤有重要的影响。为此,学者们[45,68]研究了加载波形对层裂的影响,包括方波或三角波,不同的上升沿(如准等熵加载、冲击加载)以及不同峰值应力和卸载应变率等对层裂损伤的影响。Koller 等[45]发现在同样的冲击压力下,准等熵加载下的层裂强度与方波加载类似,都明显低于三角波加载。Gray 等[69]发现在316L 不锈钢中,形成层裂损伤需要14.5 GΡa 的泰勒波(三角波),然而压力为6 GΡa、脉冲时间为0.9 µs 的方波也可以导致层裂损伤,并且方波加载时的层裂强度低于三角波加载。三角波加载可视为脉冲时间为零的方波,在这些研究中,峰值应力效应、脉冲时间效应、应变率效应耦合在一起,没有通过控制变量法一一厘清。Cai 等[70]采用分子动力学方法模拟了液体铜的层裂现象,也发现层裂面处形成的拉伸脉冲幅值在向自由面传播的过程中发生衰减,导致液体铜在方波加载下的层裂强度低于其在层裂面处承受的最大拉应力。因此,相比于方波加载,泰勒波更适合用声波方法对层裂强度进行测量。
3.2 脉冲宽度
在平板撞击实验中,样品中的冲击波脉冲或测得的自由面速度剖面通常不是标准的方波,而Hugoniot 状态的持续时间通常定义为脉冲时间。早期的研究认为,层裂强度与脉冲的持续时间τ负相关[7–8,45,69],Butcher 等[8]提出积分形式层裂强度 σsp(t)的判断准则

式中:K和α为材料属性相关的常数, σn为材料损伤成核所需的临界应力。这一准则称为损伤累积准则,即损伤累积到一定程度才会发生层裂,可以通过高应力或长脉冲时间实现。然而,Johnson 等[7]发现低压下无氧铜的层裂强度受脉冲宽度的影响较小。类似地,Li 等[28]认为低压下层裂可以在拉应力脉冲平台处形成,且脉冲宽度只能决定低碳钢的层裂是否产生,对层裂强度并没有显著的影响。如图10 所示(df和ds分别为飞片和样品的厚度),Shot 1 和Shot 2 实验的应力幅值和应变率基本相同,仅脉冲宽度差异较大,但二者却具有相同的速度差Δu,即相同的层裂强度。这些差异可能是由于研究脉冲宽度对层裂强度的影响[7–8,45,69]时忽略了峰值应力的变化。

图 10 低碳钢的自由面速度历史[28]Fig. 10 Free surface velocity histories of mild carbon steel[28]
3.3 应变率
类似材料在准静态加载下的强度均具有应变率效应,即材料层裂强度也有明显的应变率效应。如图11 所示,钛、不锈钢、低碳钢、铜和铝[8,43,71–74]等金属材料的层裂强度表现出较显著的应变率效应。层裂强度一般可以描述为应变率ε˙的指数函数

式中: σ0为拟合参数,n为应变率敏感系数。层裂强度的应变率效应可以用损伤累积准则解释,并已通过物理模型证实[8,72]。然而,Johnson 等[7]结合实验和模拟指出应变率对多晶铜的初始层裂强度有很微弱的影响。此外,Li 等[28]选取低碳钢开展系统的层裂实验,结果表明:当冲击压力为8.3 GΡa 时,层裂强度有明显的应变率效应,应变率敏感系数较大;当压力为3.2 GΡa 时,层裂强度的应变率效应大幅减弱。这些数据说明层裂强度的应变率效应与压力范围有关。

图 11 金属材料的层裂强度与应变率的关系[28]Fig. 11 Spall strength of metallic materials as a function of strain rate[28]
3.4 峰值应力
冲击波的峰值应力通常表现为冲击压力或强度,对于多数金属材料,如低碳钢、不锈钢、铜、铝等材料[5,17,28,43,75–79],层裂强度通常随冲击压力的增加而增加,这种差异有时候会被归因于冲击诱发的应变硬化效应。然而,Stevens 等[77]通过在AISI 1020 低碳钢样品背面加上不同阻抗的窗口,在固定拉应力历史不变的同时实现了2.2~11.6 GΡa 的冲击压力,研究发现层裂强度几乎不随冲击压力的上升而变化,说明层裂强度受到冲击硬化的影响较弱。类似地,Wang[78]的研究表明,随着冲击压力的增加,20 钢的层裂强度几乎不变。
峰值应力的增加往往伴随应变率的增加。Li 等[28]为了辨别峰值应力σH对层裂强度的影响是否存在应变率效应,将实验测得的层裂强度与通过应变率效应(式(4))预测的层裂强度进行比较,将层裂强度随峰值应力的变化划分为3 个阶段(见图12):在阶段Ⅰ(2.6~4.3 GΡa),实验测得的层裂强度随着峰值应力的增加而增加,但是明显低于预测值;在阶段Ⅱ(4.3~8.3 GΡa),层裂强度缓慢增加,实验值和预测值比较符合;在阶段Ⅲ(高于8.3 GΡa),随着峰值应力的增加,实验值下降比较明显,且低于预测值。3 个阶段呈现出截然不同的规律,相关解释涉及载荷参数和微结构,将在下文中详细阐明。
3.5 加载历史
层裂过程中损伤的成核、长大和联合受拉应力历史的影响。此外,层裂损伤前,冲击载荷引起的塑性变形,如位错和晶界,亦对损伤的演化产生影响。因此,根据不同的作用机制,可将载荷参数对层裂的影响分解为拉应力历史和冲击诱发的微结构两方面。
根据损伤累积准则[80],绘制了拉应力历史对层裂强度影响的示意图(见图13)。当拉应力 σ(t)超过裂纹成核所需要的临界应力 σn时,损伤开始积累。当拉应力脉冲上升沿的能量不足以使损伤度达到临界值,则层裂在后续的拉应力平台处发生,此时层裂强度是拉应力脉冲的峰值应力,并且随着冲击压力的增加而增加,与拉伸脉冲上升沿的应变率无关,无明显的应变率效应,对应于图12 中阶段Ⅰ层裂强度的实测值小于应变率效应预测值。当拉应力脉冲上升沿的能量足以使损伤度累积到临界值,则层裂发生在拉应力上升沿,层裂强度随着上升沿斜率的增加而增加,表现为明显的应变率效应,对应于图12 中阶段Ⅱ层裂强度实测值近似等于应变率效应预测值。

图 12 低碳钢层裂强度与峰值应力的关系[28]Fig. 12 Spall strength of mild carbon steel as a function of peak compression stress[28]

图 13 拉应力历史对层裂强度影响的示意图[28]Fig. 13 Schematic illustration of the effect of tensile stress history on spall strength[28]
上述讨论表明,低压方波加载下层裂强度为拉应力脉冲的峰值应力,受冲击压力和拉伸状态方程的影响较大,而与材料的微结构关系不大,此时层裂强度不能用于表征微结构对层裂损伤的抵抗能力。例如,具有不同晶粒尺寸或织构的金属材料受低压方波冲击加载时,表现为具有不同的层裂信号回跳时间、回跳斜率和不同的损伤度,而层裂强度却基本相同。这是由于微结构对损伤演化有决定性作用,但是低压下对层裂强度的影响较小。因此,如果用层裂强度表征材料对层裂损伤的抵抗能力,应避免层裂发生在拉应力脉冲平台的情况,可以采用泰勒波加载。
冲击压力较低时,金属材料的层裂损伤往往沿着弱区扩展,如低压下低碳钢[47]和铝合金[11]的损伤表现为脆性裂纹。当冲击压力较高时,层裂损伤倾向于以尽可能高的速率实现损伤度的增殖(或以较大的速率释放静水拉应力),损伤模式表现为孔洞长大。此外,随着冲击压力的升高或脉冲时间的增加,冲击导致的微结构[31,81–82]通常会发生变化,进而引起层裂强度的增加或降低。例如,Li 等[28]发现高压下低碳钢的层裂强度小于应变率效应的预测值(图12 阶段Ⅲ),且层裂强度的减少量与冲击压缩形成的孪晶密度呈线性关系(见图14),结合孔洞或裂纹在冲击诱发导致的孪晶界处形核,认为冲击诱导的孪晶界会降低低碳钢的层裂强度。另外,对于延性金属,冲击诱发的微结构有可能因应变硬化效应阻碍损伤的长大,引起层裂强度的增加。总之,冲击诱发的微结构与拉应力历史影响层裂强度的机制不同,两种效应加以区分,不能混为一谈。

图 14 低碳钢层裂损伤的微结构表征及层裂强度的减少量Δσtw与孪晶密度的关系[28]Fig. 14 Microstructure characterization of spallation damage for mild carbon steel,and reduction in spall strength Δσtw as a function of deformation twin density[28]
3.6 层裂损伤模型
建立合理的损伤演化模型来模拟预测层裂过程是研究冲击载荷下金属材料的变形损伤的重要方法。在考虑加载特征和微介观结构效应的动态损伤模型中,微孔洞成核、成长和聚集是目前普遍认同的损伤演化模式。早期Curran 等[83–84]基于层裂回收样品损伤的统计数据,构建了NAG(Nucleation and growth)模型,用于描述微孔洞的成核和长大过程。NAG 模型取得了很大的成功,然而该模型的经验性强,且拟合参数过于繁复。
理论模型一般认为损伤在静水拉应力下材料的缺陷处成核,其生长由黏性或惯性效应主导[84–87],其聚集的开始条件为达到临界孔隙度[88–89]。白以龙等[90]分析了微损伤演化的一般规律,根据微损伤数目平衡原理,结合微损伤的演化动力学,得到了微损伤成核密度演化的微分方程。
微孔洞长大过程一般通过空心球壳模型研究。Gurson[91]研究了在轴对称载荷作用下刚塑性材料中单个球形孔洞的准静态生长过程,得到了含损伤材料的塑性本构方程。Tvergaard[92]、Benzerga 等[93]将孔洞形状的影响和基体材料本构模型唯象地引入Gurson 模型,获得了Gurson-Tvergaard-Needleman(GTN)模型。GTN 模型是计算力学领域的基本损伤演化模型之一,已编制成程序模块嵌入ANSYS 等大型有限元商业软件,作为预测模型工具应用于许多工程问题。
Johnson 等[7]首先用描述孔洞准静态生长的GTN 模型模拟了无氧铜的平板撞击实验(层裂实验),模拟结果与实验结果符合很好。后续的学者沿着这一思路并结合晶体塑性[79]、非晶塑性[94]以及与动态变形相关的黏性[86–87]、惯性[86–87]、应变硬化[95]和热软化[96–97]的影响,建立了在动载荷下损伤演化模型。Wilkerson 等[79,87,94]用这些模型计算得到了层裂强度与应变率、峰值应力的关系。
封加波[98]和王永刚[99]认为,孔洞长大过程中增加的表面能和塑性功由孔洞周围球壳中基体材料的弹性能提供,由能量守恒得到微孔洞生长方程,建立层裂损伤度函数模型,并把该模型应用到有限元中,得到了与层裂实验样品自由面速度曲线吻合较好的曲线。
4 结 束 语
对于组分或晶体结构相似的金属材料,不难发现微结构和加载特征对层裂强度的影响往往大相径庭,且相关的机理解释众说纷纭。由于材料本身的塑性变形及力学性质的各向异性,不同单晶材料的层裂强度呈现出明显的各向异性。多晶材料中有较多的缺陷,由于缺陷是材料损伤的成核源,因此缺陷分布的各向异性导致了损伤演化的各向异性。但该各向异性会随着冲击压力的升高逐渐趋于各向同性。高能量晶界和相界容易成为损伤的成核源,进而影响金属材料的层裂强度。针对目前层裂强度的测试方法,泰勒波加载能获得更准确的层裂强度数据。脉冲宽度只决定层裂是否产生,对层裂强度无明显影响。金属材料层裂强度具有明显的应变率效应,但应变率效应与压力范围有关。层裂强度随冲击压力的增加而增加,达到某一阈值时,层裂强度几乎不变。除此之外,冲击诱发的不同微结构影响层裂强度的机制不尽相同。
上述现象很大程度上是由于微结构和加载特征对层裂强度的影响具有如下复杂性:(1) 脉冲时间、峰值应力和应变率经常耦合在一起,改变其中一个参数,其他参数通常也随之变化;(2)拉应力与时间的对应关系近似呈梯形,如果层裂在平台处形成,通常表现为方波加载的初始层裂,此时层裂强度为平台处的拉应力幅值,受微结构的影响较小;(3)材料在冲击压缩阶段和层裂前的拉伸阶段均会发生塑性变形,因塑性变形形成的微结构对延性材料,尤其是单晶延性材料的损伤成核和生长的影响较大,同时亦受加载特征的影响;(4)层裂信号向样品自由面传播时会发生衰减,传播距离越大,通过自由面粒子速度计算得到的层裂强度越偏离真实值,为获得准确的层裂强度,可采用泰勒波加载。
微结构和加载特征对金属材料层裂强度的复杂影响难以通过实验完全阐明,这给变形损伤模型的发展提供了新的研究方向。目前,层裂损伤模型多为基于经验和平均场的唯象模型,很少涉及与微结构相关的变形损伤机制。因而,基于实验观测的微结构、加载特征和变形损伤行为,建立冲击载荷下金属材料的微结构-加载特性-层裂响应关系,发展基于物理的变形损伤模型对预测工程装置的服役表现具有重要的意义。

