债券久期和凸性的计算方法探讨

□蒋崇辉 马永开

[电子科技大学 成都 610054]

引言

修正久期和凸性是债券和债券组合管理的核心概念，是衡量债券及债券组合利率风险的重要工具[1~4]，是投资者执行各种债券投资策略和套期保值策略的重要基础[5~7]。商学院学生在学习银行管理和投资方面的课程时通常都有关于久期和凸性的内容。然而，笔者在教学实践中发现，为数不少的同学都无法真正理解这两个概念并进行灵活运用。究其原因，教师在讲授久期和凸性的概念时，一方面，久期会涉及有“麦考利久期”和“修正久期”的双重使用；另一方面，凸性的概念带有较强的技术性，在同学们缺乏对这些概念的感性认识时，很难做到透彻理解这些概念，更不用说灵活运用。

债券的久期就是投资者收到债券各个现金流所需时间的加权平均，权重为各个现金流现值占所有现金流现值的比重。这个概念最早由弗雷德里克·麦考利引入，所以，我们通常称之为麦考利久期。很显然，由于麦考利久期是时间的加权平均，所以，麦考利久期是用“年”来衡量的。对于普通债券而言，其麦考利久期通常介于0和债券存续期之间，特别地，零息债券的麦考利久期就等于其存续期。麦考利久期虽然衡量了投资者收到各个现金流的所需要的平均时间，但对于利率敏感型的债券而言，投资者更需要知道债券价格相对于利率变化的敏感性，即债券的利率风险，而衡量这个的敏感性的指标就是修正久期。从概念上看，麦考利久期衡量的是投资者收到各个现金流的平均时间，以“年”为单位，而修正久期则描述的是债券价格相对于利率变化的敏感性。敏感性是没有单位的，因此麦考利久期和修正久期分别描述了债券的不同性质。在计算方法上，计算麦考利久期使用的是债券的到期收益率[8~11]，即对债券的每个现金流都用相同的折现率进行折现得到。然而，由于修正久期需要抓住利率变化所导致的债券价格的变化，因此，为了准确计算修正久期，对债券的每个现金流都会用对应期限的折现率进行折现。而不同期限的折现率会存在差异，另外，基准利率的变化所导致的不同期限的利率变化也会存在不同。因此，现有教材上将修正久期直接写成对麦考利久期的一个修正，这会严重误导同学们对修正久期的理解！最后，由于修正久期描述的是债券价格相对于利率变化的敏感性，在债券组合管理过程中，修正久期的应用远多于麦考利久期。正因为以上几方面的原因，本文主要考察了定期复利计息①情况下债券和债券组合修正久期的计算问题。

在利率变化幅度很小的情况下，修正久期基本上能抓住利率变化所带来的债券价格的变化。然而，由于债券的价格收益率曲线的形状是凸形的，如图1所示。这种凸形特征决定了当利率变化幅度较大的情况下，修正久期并不能完全抓住利率变化所导致的债券价格的变化。在这种情况下，为了更准确衡量利率变化导致的债券价格变化，就需要考虑债券的凸性。具体而言，修正久期对应的是债券价格相对于利率的一阶导数，而凸性对应的则是二阶导数，这与期权市场上用来刻画期权风险的德尔塔和伽马对应②。所以，本文除了考察债券和债券组合修正久期的计算问题以外，还考察了债券和债券组合凸性的计算问题。

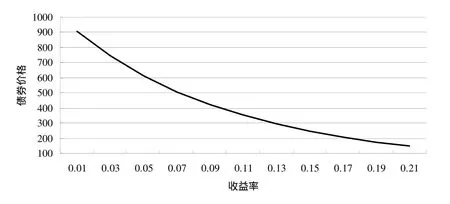
图1 债券价格收益率曲线

综上所述，债券修正久期的本质是债券价格相对于市场基准利率变化的敏感性，由于债券价格并不是其收益率的线性函数，所以，当市场基准利率变化较大的情况下，作为债券价格相对于收益率二阶导数的凸性应该被纳入以改善修正久期的业绩。本文从债券修正久期和凸性的本质出发，通过计算零息债券修正久期和凸性，给出了付息债券或债券组合修正久期和凸性的计算方法。

一、修正久期

（一）零息债券的修正久期

首先我们从零息债券的价格及其价格相对于利率变化的敏感性说起。假设某n年后到期的零息债券的面值为Par，则该债券的价格P应该为

式(1)中的in即为该零息债券的到期收益率，也就是期限为n年的即期利率。对于信用级别相同期限不同的零息债券而言，他们的到期收益率与期限之间的关系就表现为该信用级别债券的即期利率曲线。图2描述的是2011年9月1日中国固定利率国债收益率曲线。

当市场基准利率发生变化，会导致各期限即期利率也发生变化，进而会带来收益曲线的移动。由式(1)可知，在即期利率发生变化的情况下，债券价格也会发生变化，对债券投资者而言，把握债券价格相对于利率变化的敏感性显得非常重要。债券价格相对于利率变化的敏感性可通俗表述为利率变化一个基点会导致债券价格变化多少个基点。为了揭示这个敏感性，我们对式(1)两边求微分有

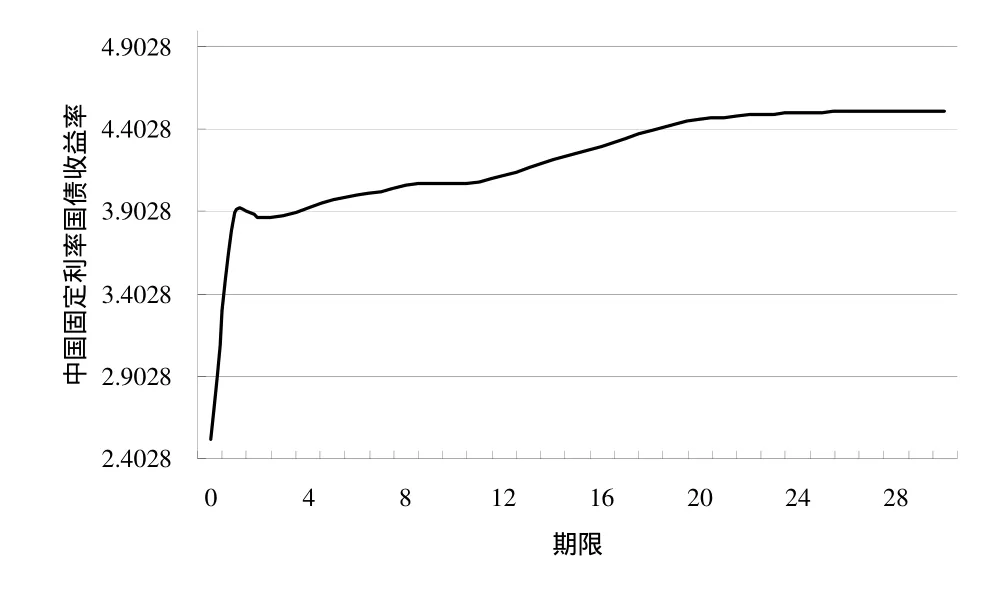
图2 中国固定利率国债收益率曲线（数据来源于中国债券信息网）

其中Ru即为利率变化所带来的债券价格变化的百分比，也就是利率变化给投资者带来的非预期收益率，而Δi即为利率的变化，DMn即为n年期零息债券的修正久期。从式 (4)可以看出，零息债券的修正久期就是用 1 +in进行调整之后的久期，显然，修正久期揭示了债券价格变化相对于利率变化的敏感性。例如，对于修正久期为0.97的零息债券而言，利率变化10个基点，债券价格变化为9.7个基点，从这个意义讲，债券的修正久期与股票的贝塔以及期权的德尔塔类似。

（二）附息债券和债券组合的修正久期

考虑一只两年期每年付息一次的附息债券，设该债券一年后的现金流为C1，两年后的现金流为C2+Par，则该债券的价格应该为

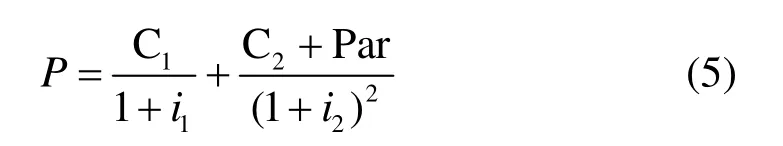
式(5)中i1、i2分别为与该附息债券信用级别相同的一年，两年期即期利率。我们知道，任何附息债券均可以看成多个零息债券的组合。对于上述两年期附息债券而言，可以视为面值为C1的一年期零息债券与面值为C2+Par的两年期零息债券的组合，因而该附息债券的价格应该为这两只零息债券的和，即

其中DM就是这两年期附息债券的修正久期。从上面的推导过程可以看出：在收益曲线平行移动的情况下，附息债券的修正久期是债券各现金流修正久期的加权和，权重为各现金流现值占附息债券价格的百分比；同理，债券组合的修正久期也是组合中各债券修正久期的加权和，权重为各债券价值占债券组合总价值的百分比。

二、凸性

在利率变化幅度很小的情况下，修正久期基本上能抓住利率变化所带来的债券价格的变化。然而，由于债券的价格收益率曲线的形状是凸形的，这种凸形特征决定了当利率变化幅度较大的情况下，修正久期并不能完全抓住利率变化所导致的债券价格的变化。在这种情况下，为了更准确衡量利率变化导致的债券价格变化，就需要考虑债券的凸性。

（一）零息债券的凸性

仍然以n年期的零息债券为例，对债券价格在当前n年期即期利率进行泰勒展开可以得到：

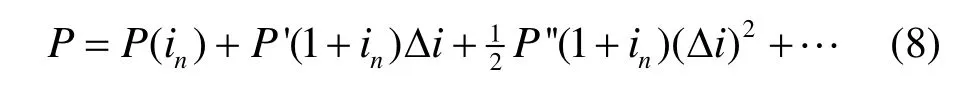
从式(10)可以看出，在忽略债券凸性的情况下，根据久期所计算得到的价格变化会存在高估或者低估的偏差。如果利率上升，则会高估债券价格下跌的幅度，而在利率下跌的情况下，则会低估债券价格上涨的幅度。

（二）附息债券和债券组合的凸性

不管是附息债券还是债券组合，均可以看成一系列零息债券的组合。根据“组合收益率是组合中各成份证券收益率加权和”的基本原理，我们可以得到附息债券或债券组合价值变化的百分比Ru为

三、实例分析

修正久期和凸性的一个基本应用在于预测利率变化所导致的债券价格以及债券组合价值的变化，进而为投资者制定债券投资策略以及风险管理提供依据。下面以一个简单的例子阐述根据本文方法计算修正久期和凸性，进而预测债券价格的变化。

设某投资者持有六年后到期的票面率为8%的附息债券，其中票面价值为1000元，假设1～6年期即期利率分别为6.0%、6.5%、7.0%、7.5%、8.0%、8.5%。设利率上涨1%，即期利率曲线向上平移1%，我们根据前文所介绍的方法首先在EXCEL表格中分别计算附息债券各现金流的现值，各现金流现值占比，各现金流的修正久期以及凸性，如表1。

由于附息债券的修正久期和凸性分别是各现金流修正久期和凸性的加权和，因而可以通过EXCEL中的SUMPRODUCT函数求得附息债券的修正久期为4.5790，凸性为27.5876。如果仅仅利用修正久期这个工具，则利率上升1%应该导致债券价格下跌4.5790%，如果同时利用修正久期和凸性两个工具，则利率上升1%导致债券价格下跌的百分比为4.4411%③。

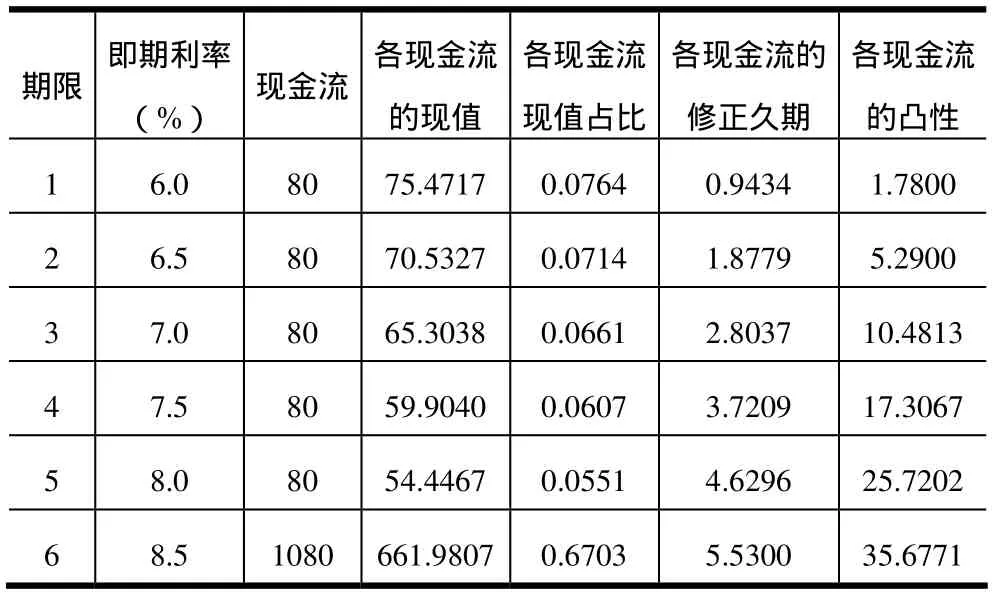
表1 附息债券各现金流修正久期和凸性的计算

为了进一步验证同时利用修正久期和凸性两个工具所预测的债券价格变化比单独使用修正久期预测得到的债券价格变化更接近实际债券价格的变化，我们分别计算了利率变化前后附息债券的理论价格。利率变化前附息债券的理论价格为表1中各现金流现值之和，为987.6397元，而利率变化后的理论价格为943.7459，理论价格下跌4.4443%。显然，同时利用修正久期和凸性两个工具所预测的债券价格变化更接近债券理论价格的变化。

四、小结

通过辨析债券的麦考利久期和修正久期在概念和计算方法上的差异，本文指出修正久期才是债券和债券组合风险管理的核心工具。由于债券价格并不是收益率的线性函数，当利率变化幅度较大的情况下，修正久期不足以抓住利率变化所带来的债券价格的变化，所以，债券的凸性应该被纳入以改善修正久期的业绩。从修正久期和凸性的本质出发，通过计算零息债券修正久期和凸性，给出了付息债券或债券组合修正久期和凸性的计算方法，并通过实例阐述了债券修正久期和凸性的计算及应用。实例表明，本文给出的债券久期和凸性的计算方法吻合债券久期和凸性的定义，而且计算方法清晰明了，在EXCEL中计算简便，不仅可以帮助我们理解修正久期和凸性的概念，还能推广到更一般的情形。

注释

①定期复利计息是对“periodically-compounded”的翻译，如半年计息一次或一年计息一次，这是与债券市场上半年或一年付息一次的情况对应的。

②期权的德尔塔是衡量期权价格相对于标的资产价格的敏感性，而伽马衡量期权德尔塔相对于标的资产价格的敏感性，因此德尔塔是期权价格相对于标的资产价格的一阶导数，而伽马是期权价格相对于标的资产价格的二阶导数。

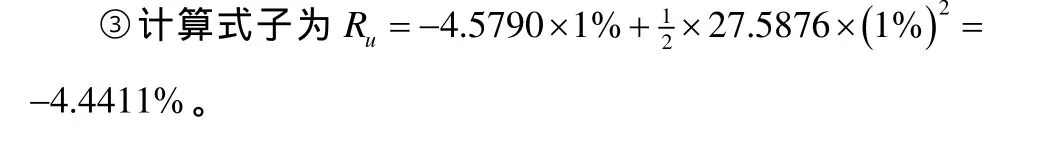
[1]林清泉，李锦涵.基于债券久期思想对投资回收期法的改进[J].中南民族大学学报(自然科学版), 2011,30(2):119-123.

[2]王炜辰，叶秩.含权债券久期计算及其在风险管理中的应用[J].中国证券期货，2010(5):36-38.

[3]刘向丽，程刚，成思危，汪寿阳，洪永淼.中国期货市场价格久期波动聚类特征研究[J].管理科学学报，2010,13(5): 72-81.

[4]祎张瑞君，李子 ，熊春月.运用久期模型进行利率风险管理[J].财务与会计，2010(8):16-18.

[5]刘艳萍，涂荣，迟国泰.基于方向久期利率风险免疫的资产负债组合优化模型[J].管理评论，2009,12(4):11-33.

[6]刘艳萍，涂荣，迟国泰.基于信用风险久期免疫的资产负债管理优化模型[J].管理学报，2010, 7(2):278-288.

[7]杨哲，董炜琛.久期、利率免疫与商业银行资产负债管理[J].财经政法资讯，2006(5):39-42.

[8]HULL J C.Options, Futures, and Other Derivative Securities (Second ed.)[M].Englewood Cliffs, NJ: Prentice-Hall,Inc., 1993: 99-101.

[9]BREALEY R A, MYERS S C, FRANKLIN A.Principles of Corporate Finance (Tenth ed.)[M].New York, NY:McGraw-Hill Irwin, 2011: 50-53.

[10]MARRISON C.The Fundamentals of Risk Measurement[M].Boston, MA: McGraw-Hill, 2002: 57-58.

[11]JONATHAN B, PETER D.Corporate Finance(Second ed.)[M].Boston, MA: Prentice Hall, 2011: 966-969.