基于GPU的遗传退火多序列比对并行研究

韦树烽，刘 羽，蒋财运

（1.桂林理工大学广西矿冶与环境科学实验中心，广西桂林541004；2.桂林理工大学机械与控制工程学院，广西桂林541004；3.桂林理工大学信息科学与工程学院，广西桂林541004）

0 引 言

在生物信息学中，多序列比对（multiple sequences alignment）是一种基本的生物信息处理方法，在发现生物序列的结构、功能和进化的信息方面具有重要意义［1］，它是一个尚未有效解决的NP完全的组合优化问题。生物科学的不断发展使得GenBank、EMBL、DDBJ等序列数据库容量快速增长。截止2013年2月GenBank库核酸序列已超过1.6亿条，碱基对超过1.5千亿对［2］。对于序列比对的结果评估具有计算速度和最佳敏感度两个标准［3］，设计一个合理高效的序列比对算法是一个重要的研究方向。

为了提高比对效率，并行计算技术被应用到该领域。目前主要有BLAST、FASTA、Smith－Waterman和CLUSTALW等MSA的并行处理策略［4－7］。由于近年来GPU应用于并行计算领域上的优势，国内外众多测序比对软件都在尝试基于GPU的平台进行研发。而本文主要工作就是基于CUDA模型研究遗传退火多序列比对算法的并行加速模型，为生物信息研究分析提供支撑。

1 多序列比对算法

1.1 多序列比对算法数学描述

表1 多序列比对示例

1.2 遗传模拟退火多序列比对算法概述与设计

在MSA算法中，主要有动态规划法、渐进算法、迭代算法等。其中遗传模拟退火多序列比对算法（SAGAMSA）是迭代算法中的典型全局比对算法，具有极高计算复杂性［8］。它通过精细迭代方式来实现多序列比对，利用模拟退火策略对遗传操作进行改进使MSA可以获得更好的效果，同时具有很好的鲁棒性、对序列个数不敏感和不易陷入局部最小的特性。SAGA－MSA可以定义为一个8元组［9］

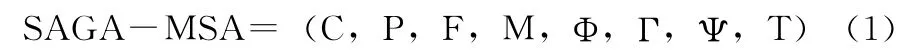
式中:C——个体的编码方式，P——初始种群，F——个体的适应度评价函数，M——种群大小，Φ——选择退火算子，Γ——交叉退火算子，Ψ——变异退火算子，T——终止退火条件。下面简要介绍本文几个关键点:

（1）本文采用可变长的二维矩阵编码方式，由1.1节知m条序列比对结果是一张m＊n矩阵，编码矩阵为SEQ′ij（0＜i＜m，0＜j＜n），这种编码方式具有简单直观、易于操作的优点。

（2）初始化种群是SAGA－MSA搜索寻优的出发点，本文采用随机产生初始种群方法，对长度为Li（0＜i＜m）的SEQi（0＜i＜m）随机选择不大于Li的整数Xl（0≤l≤n－Li），在序列Xi位置插入“－”使得比对结果每条序列的长度都为n。

（3）SAGA－MSA的适应度函数采用SP目标函数，函数值越大则种群个体的质量越好，进入下一代的概率就越高。目标函数是总评分减去空位仿射罚分［10］，总评分中，两个空位符匹配评分为0，两个非空位字符匹配时参照Blosum62评分矩阵［11］，空位与其它字符的比对评分值为－5。空位仿射罚分中，空位开放罚分为10，空位延伸罚分为0.2。

（4）选择退火算子是在遗传操作中加入了退火策略，采用Metropolis接受准则。为了保持种群多样性，操作中不删除适应度不够好的种群个体。以概率pnew接受新一代个体，保存当代最佳个体

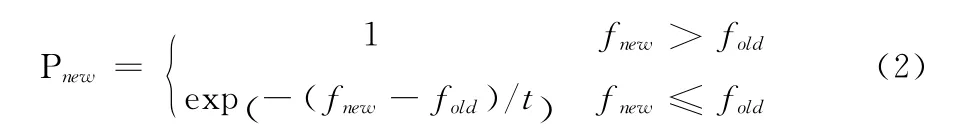
式中:f——适应度函数，t＞exp（t＊alpha），（alpha为温度变化系数）为退火温度控制参数。

在农业机械化法律关系中，出现了责任主体和监督主体不明晰的现象。目前在全国范围内，我国尚未建立一个完善的农业机械安全管理法律制度。针对农机管理部门对农业机械的初次检验、年度检验和临时检验；农业机械的停驶登记、报废登记；农业机械驾驶操作人员的考核、安全教育、证照核发、变动登记、年审、农机违章和责任事故的处理等一系列的问题在各个地区之间存在的差异不大，可以在全国范围内确立统一的标准，由政府主管的农业部门作为主要监管机构，联合交通运输部门和公安部门，形成一个较为完善的农业机械管理体系，对农业机械化的安全管理问题明确一个相对清晰的责任划分，方便农业机械的安全管理。

（5）交叉操作是将老一代的序列进行重组，形成优秀的序列遗传到新一代。本文采用两点交叉的遗传操作，对老一代种群个体随机从［0，Li－1］（0＜i＜m）中选取两个整数rand1＞rand2作为交叉位置，以概率pnew对个体进行交叉操作产生新代。

1.3 SAGA－MSA算法串行测试与分析

根据1.2节的描述对SAGA－MSA实现串行算法如下:

对上述串行算法各阶段耗时分析，测试数据来源于GenBank的序列文件gbbct1.fsa＿aa中随机抽取的2048条序列，平均长度为256。设定初始参数种群数为5、迭代次数为5、初始温度为10、温度变化系数为0.5、终止温度为1。测试结果见表2，算法的第三、四阶段耗时比例较大，占用大部分的计算时间。

表2 SAGA－MSA串行算法各阶段耗时百分比

2 GPU架构和CUDA编程模型

自2007年NVIDIA推出通用并行计算模型CUDA以来，GPU（图形处理器）能够解决复杂计算问题而被应用到高性能并行计算领域。CUDA是用于GPU计算的开发环境，它是一个全新的软硬件架构，包含CUDA指令集架构（ISA）和GPU内部的并行计算引擎两部分［12］。在CUDA的模型中可以将GPU视为一个并行数据计算设备，对计算进行分配和管理，具有并行效果明显的特点。

在本文并行模型中，GPU专注于复杂的并行处理计算。由于CUDA内部并行机制的多级性，算法采用任务分解方式，将需要并行处理的粗粒度任务划分成相对独立的模块，不同模块由不同的GPU线程块处理，同时尽量减少通信。线程块内由多个处理线程进行细粒度的计算。因此如何准确划分合理的求解粒度和解决模块间通信问题是我们研究的重点。

3 SAGA－MSA算法并行化分析与实现

本文的研究目标是在保持序列比对结果在一定的敏感度的前提下，提高其比对效率。SAGA－MSA算法并行化的关键技术难点在设计合理的并行粒度划分策略，解决并行线程的通信延迟问题、保持良好的负载平衡，以此保证MSA并行化实现的合理性和高效性。

3.1 算法并行化分析

表2的串行分析结果显示，算法的stage 3和stage 4耗时最为明显，当数据集很大时，stage 1、stage 2和stage 5几乎可以忽略不计。因此本文主要针对stage 3和stage 4这两阶段的运算进行并行化。SAGA－MSA算法继承了自然进化过程中固有的并行性，算法中的迭代不是从单个解开始计算，而是从问题解集（种群）开始。计算过程从一组解迭代到另一组解，能够同时处理群体中多个个体，易于并行化。而本文拟采用SAGA－MSA的种群计算的粗粒度模型（coarse－grained model）［13］结合多序列比对中固有的细粒度模型（fine－grained model）来研究算法的并行化实现。

在SAGA－MSA中，粗粒度并行模型就是种群中若干个体并行计算，如图1所示。每个个体分配对应的线程块执行并行运算，每个线程块进行独立的选择、交叉和变异操作和适应度计算。定期地相互传送适应度最好的个体，加快满足终止条件的要求。这样算法的并行化在不同的种群规模时都以较小的通信开销获得了更好的加速。

图1 SAGA－MSA的粗粒度并行模型流程

由于MSA是双序列比对的拓展，具有天然并行性［14］。根据两条序列比对与另两条序列比对的数据不相关特性，可是确定多序列比对的细粒度模型。既是从m条序列SEQ′ij（1≤i≤m－1，0＜j＜n）中选择的SEQ′ij与SEQ′（i＋1）j成为一组比对，这样比对组数是m＊（m－1）/2。分别对每一组分配不同的处理线程进行处理来实现并行化，如图2所示。相对于串行的循环比对各组的最大优点就是可以实现同时对多个组并行处理，理论上只要有足够的处理核，可以实现很好的加速效果。

图2 SAGA－MSA的细粒度并行策略

同时细粒度模型还有一层数据处理并行化，例如图2的SEQ′4j和SEQ′5j（j＝1，2，…n）两条序列比对时进行并行化，它们的第j对氨基酸比对，用两个线程分别对两条序列各自搜索实现并行处理。另外，在对m条序列生成比对矩阵时每条序列操作也都是并行操作的。

当然算法的并行化研究还需根据输入数据本身的特点进行合理并行化。因此选择输入序列的种群规模p和序列条数m是处理核的整数倍时，理论上能达到较好的负载均衡。另外输入序列的平均长度也影响着负载均衡，假如对输入序列长度引入数学期望E，有E增大，则线程块和线程处理等待同步操作时耗时增加，各并行处理线程能达到的负载均衡变差，序列比对效率有所下降。

3.2 算法并行化实现

算法的并行化代码是C/C＋＋结合CUDA编程模型的开发语言。结合CUDA内部并行机制与3.1节分析的并行方式设计了合理的三层并行算法。CUDA提供了HOST端调用DEVICE端的全局函数（＿＿global＿＿），调用格式例如调用函数change＜＜＜dimBlock1，dim Thread1，smem－Size1＞＞＞（），其中change函数是1.3第五点实现的种群交叉操作。CUDA中在每个线程块的执行宽度warp是32个线程，线程数的设置为32的倍数能达到最好效率。

计算适应度Fitness函数（如图3所示）是并行实现的重点，函数的并行性能直接影响并行效率。这一阶段分为两个并行函数操作，第一个函数用CUDA线程块内的两层并行级分别同时计算m＊（m－1）/2个序列比对组的适应度并保存到数组sum12。第二个是并行规约数组sum12［m＊（m－1）/2］，在规约运算中，大部分的warp都能满载，可以有效提高效率。函数SafeTheBest的作用是找出最优的适应度并保存最优种群，根据概率pnew（见式（2））接受上一代种群。算法完成一代种群计算后，自动进入下一代的种群更新，直至满足退火终止条件得到最优适应度和种群后才退出，这相对于串行算法每计算一个种群个体都比较适应度和保存种群得到了很大的优化。

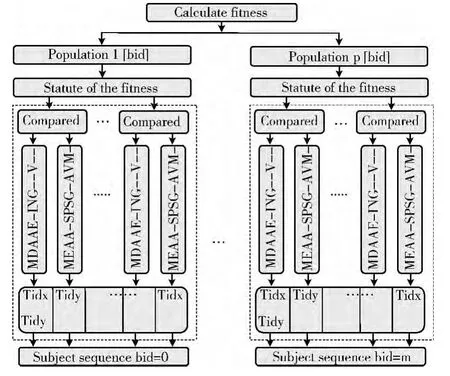
图3 Fitness函数并行实现

另外为了记录算法的各阶段和总程序的耗时情况，构建了一个精确的时钟函数，调用核函数后在HOST端用cuda Thread Synchronize（）来实现等待GPU时间同步，这样可以准确地记录程序的总耗时和各阶段的运算时间。

4 测 试

在本节中，对SAGA－MSA串行算法和并行算法进行全方面的比较。测试环境以下:CPU是3.30 GHz的英特尔酷睿i3－2120，GPU为NVIDIA GeForce 405（512MB的RAM），操作系统是Windows XP（2GB内存）。测试数据来源于GANBANK库2013年2月版的gbbct1.fsa＿aa序列数据文件。从中随机选择序列并编制了20个序列数量从8到1024测试实例。其中每个测试实例有5种序列长度，平均长度为49、99、203、227、412，比对结果的序列长度为64、128、256、450、720。为了确保两种算法的等效计算，使用了下列3组不同的起始输入参数:第一组种群大小为5、迭代次数为5、起始温度为10、退火系数为0.5、终止温度为1；第二组是第一组只增加迭代次数和起始温度到10、20；第三组是在第二组基础上只增加种群大小到20。另外为了保证结果不受系统不稳定形成的误差影响，每个实例运行5次取其平均值得到稳定的结果。

首先对两种算法的适应度（敏感度）进行比较。图4是两种算法在上述第一组输入参数情况下得到的适应度比较图，串行算法用实线表示，并行算法用虚线表示，不同的线上符号表示5种序列长度。可以观察的到，串行与并行算法的适应度分别在上述的输入序列长度各不相同时都能几乎保持一致，随着序列数量的增加，适应度都是以一定的趋势在增加。应当强调的是，因为算法的随机选择机制，SAGA－MSA并不是一个等效的算法，它们的比对结果不完全相同。因此本文的并行算法能满足与串行算法在相同敏感度的基础上研究加速的前提。

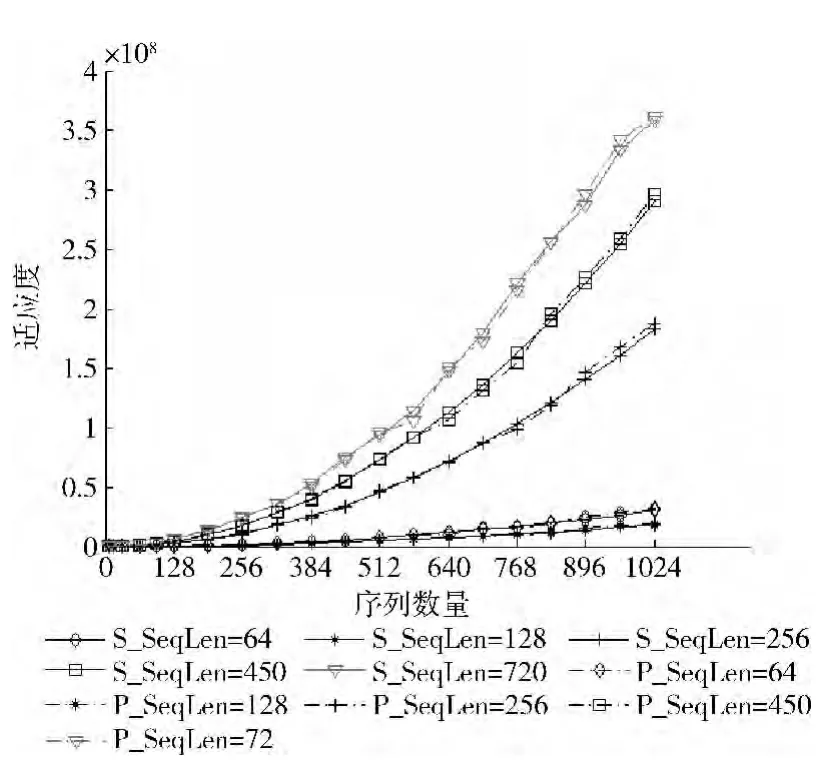
图4 串行算法与并行算法的适应度比较

图5是两种算法的总耗时的时间曲线图，执行时间以s为单位。两个算法的执行时间都是随着序列规模增大（序列数量和序列长度）而增大，显然串行算法的增长速度更快，例如序列长度为720时，它的平均输入序列长度412，则插入的平均空位数是308。可以观察到并行算法虽然在开始问题规模较小时耗时比串行的多，但是增加序列条数时耗时是平缓增加，串行耗时却增长很快，当增加到704条序列以后并行算法的耗时开始比串行的时间耗时小。

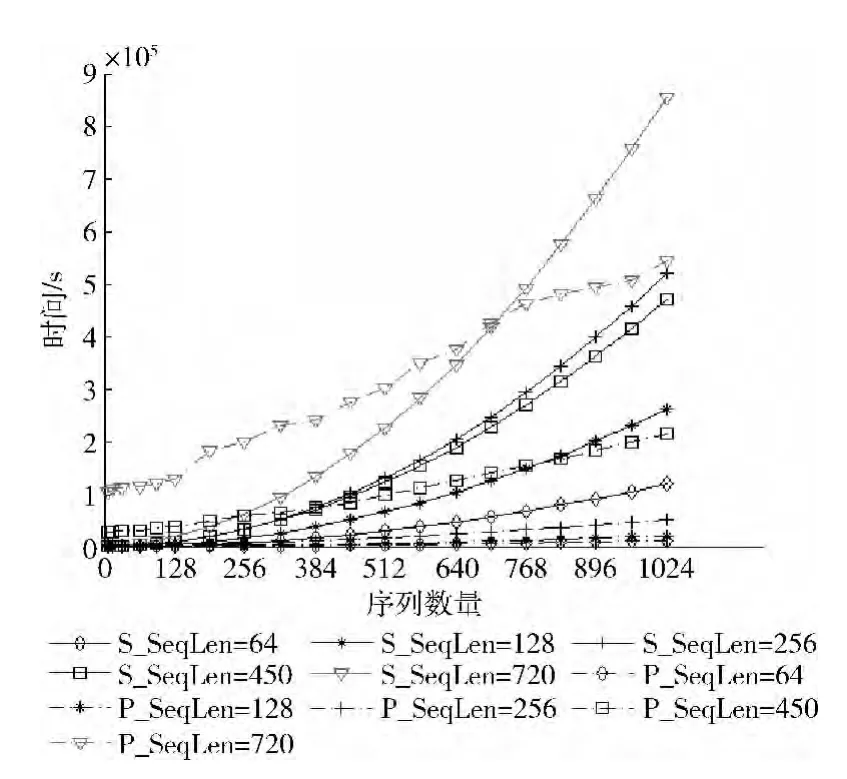
图5 串行算法与并行算法的总耗时比较

图6是两种算法耗时加速比曲线图，可以观察到不同序列规模有不同的加速比。比对结果长度如64、128、256的平均插入“－”空位数是15、29、53的加速效果明显，加速比提升较快，表明在输入序列数量不多的情况下也能有较好的加速效果，长度为128时的加速效果最明显，但是由于受限于显卡的性能，从序列数量为832后几乎是平缓增长的，并在序列数量为1024时加速比能达到12.53倍。另外对于长度为450和720插入平均空位数是223和308的加速效果不太明显，加速比只达到了2.19和1.57。影响它们的加速效果是由于输入序列的最大长度和最小长度之间的相差很大，并且有多数的长序列和短序列交杂输入，由3.1节的输入数据分析可知这样会造成在并行运算时不同的序列处理线程等待同步耗时太长。

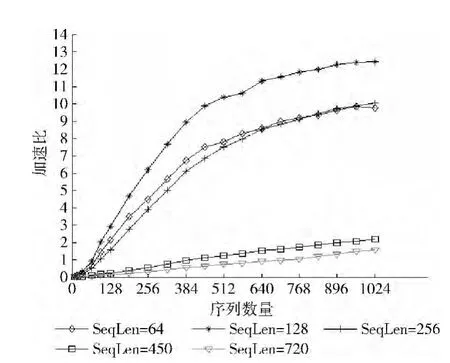
图6 串行算法与并行算法的加速比

最后，为了测试分析并行算法在增加种群数量和迭代次数对并行效率的影响，特别增加了第二、三组的参数测试，测试的加速比都与第一组的对比。在这两个测试中，发现在图7和图8的加速效果都有些许增加，图8比图7更为明显。并行算法在增加迭代次数和种群数量时都能保持良好的加速效果，且能更快达到加速极限值。如图8中，序列长度为128时加速比平均增加了0.06，并在序列数量为384时能达到最大增加值0.19，因此初始参数的设定对加速效果也有不同程度的影响。

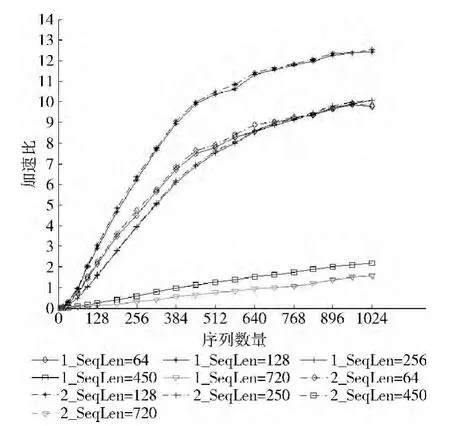
图7 增加迭代数和初始温度的加速比变化

图8 增加种群数量的加速比变化

5 结束语

本文从多个层面进行了SAGA－MSA并行化的合理性和高效性处理，采用了合理的并行粒度划分策略，并从线程同步、存储访问和负载均衡等方面对算法进行了优化，用CUDA的共享内存来缓解访存操作的竞争影响，在处理插入空位和比对空位时排除了大部分的冗余同步操作。通过在运算开始就进行数据块的初始化，减少了数据间交换引起的通信延迟问题。通过对序列插入空位位置进行排序，保证了良好的负载均衡。测试结果表明，实现的基于GPU的SAGA－MSA并行高效算法，相对于串行算法，计算速度有了明显的提升。虽然受限于测试GPU硬件性能，还是实现了12.53倍的加速比，充分发挥了GPU在并行运算中的性能优势。

下一步，将考虑引入基于消息传递的MPI和基于共享内存的OPENMP并行机制来实现多层次的混合并行模型，CPU多核和GPU众核分别负责粗、细粒度的并行计算任务。粗细粒度相结合的并行方式可以更好地利用计算资源，从而进一步提高加速比。

［1］ZHOU Hong.Research on parallel algorithm of multiple DNA sequence alignment based on de Bruijn graph［D］.Tianjin:Tianjin University，2011（in Chinese）.［周红.基于de Bruijn图的DNA多序列比对并行算法研究［D］.天津:天津大学，2011.］

［2］GenBank.Growth of GenBank and WGS［DB/OL］.http://www.ncbi.nlm.nih.gov/genbank/statistics，2013.

［3］KANG Xiaojun.Gene sequence alignment algorithm research and implement in SNP［D］.Wuhan:Huazhong Agricultural University，2011（in Chinese）.［康晓军.基因序列比对算法在SNP中的研究及应用［D］.武汉:华中农业大学，2011］.

［4］Ali Khajeh－Saeed，Stephen Poole，J Blair Perot.Acceleration of the Smith－Waterman algorithm using single and multiple graphics processors［J］.Journal of Computational Physics，2010，229（11）:4247－4258.

［5］Lars Wienbrandt，Stefan Baumgart，Jost Bissel，et al.Massively parallel FPGA－based implementation of BLASTp with the two－hit method［C］//Proceedings of the International Conference on Computational Science，2011:1967－1976.

［6］Cheng Ling，Khaled Benkrid.Design and implementation of a CUDA－compatible GPU－based core for gapped BLAST algorithm［C］//Proceedings of the International Conference on Computational Science，2010:495－504.

［7］Baomin Xu，Jin Gao，Chunyan Li.An efficient algorithm for DNA fragment assembly in MapReduce［J］.Biochemical and Biophysical Research Communications，2012，426（3）:395－398.

［8］ZHANG Yi.Based on genetic annealing bioinformatics multiple sequence alignment algorithm［D］.Chengdu:University of Electronic Science and Technology，2006（in Chinese）.［张忆.基于遗传退火的生物信息学多序列比对算法研究［D］.成都:电子科技大学，2006.］

［9］BIAN Xia，MI Liang.Development on genetic algorithm theory and its applications［J］.Application Research of Computers，2010，27（7）:2425－2429（in Chinese）.［边霞，米良.遗传算法理论及其应用研究进展［J］.计算机应用研究，2010，27（7）:2425－2429.］

［10］Chengpeng Bi.Deterministic local alignment methods improved by a simple genetic algorithm［J］.Neurocomputing，2010，73（13）:2394－2406.

［11］Jacek Blazewicz，Wojciech Frohmberg，Michal Kierzynka，et al.G－MSA－－A GPU－based，fast and accurate algorithm for multiple sequence alignment［J］.Journal of Parallel and Distributed Computing，2013，73（1）:32－41.

［12］BAI Hongtao.Research on high performance parallel algorithms based on GPU［D］.Jilin:Jilin University，2010（in Chinese）.［白洪涛.基于GPU的高性能并行算法研究［D］.吉林:吉林大学，2010.］

［13］TAN Caifeng，MA Anguo，Xing Zuocheng.Research on the parallel implementation of genetic algorithm on CUDA platform［J］.Computer Engineering and Science，2009，31（A1）:68－72（in Chinese）.［谭彩凤，马安国，邢座程.基于CUDA平台的遗传算法并行实现研究［J］.计算机工程与科学，2009，31（A1）:68－72.］

［14］YE Xiaochun，LIN Wei，FAN Dongrui，et al.Efficient parallelization and optimization of protein sequence comparison algorithm on many－core architecture［J］.Journal of Software，2010，21（12）:3094－3105（in Chinese）［叶笑春，林伟，范东睿，等.蛋白质序列比对算法在众核结构上的并行优化［J］.软件学报，2010，21（12）:3094－3105.］