化学实验室资源优化配置的探索与实践
田景芝, 荆 涛, 郑永杰, 田志茗, 杜晓昕
(齐齐哈尔大学 a.化学与化学工程学院; b.计算机与控制工程学院, 黑龙江 齐齐哈尔 161006)
0 引 言
高校中化学实验室无纸化资源管理的普及,电子化网络化的管理模式给高校带来了巨大的变革[1-2]。但随着学校化学实验教学体系的不断发展完善,实验资源(如化学药品、化学仪器和实验场地)迅速增长,如何根据教学计划对这些实验资源进行智能的优化配置成为当前亟待解决的难题[3-4]。在对资源进行合理优化配置的时候,需要考虑的制约条件会很多,人工优化配置显然不可行,因此需要找到智能优化算法来解决该问题[5-6]。粒子群算法[7]是一种较为新颖的智能仿生算法,成为了学者用来解决优化求解问题的研究热点。本文采用粒子群算法来设计化学实验室无纸化资源管理中的优化配置算法。
1 优化配置问题描述
1.1 问题模型
化学实验室无纸化资源配置问题是一个六维空间上的组合优化问题[8-9]。六维空间定义为PZ(U,L,D,I,T,P),其中,U为用户维度,L为课程维度,D为化学药品维度,I化学仪器维度、T为时间维度和P为实验室维度。每个维度包含的实体集合如下。
用户维度集合:U={U1,U2,…,Ux},Ui表示第i个用户。
课程维度集合:L={L1,L2,…,Ly},Li表示第i门课程。
化学药品维度集合:D={D1,D2,…,Dz},Di表示第i种化学药品申请数目,D*为D的子集即D*⊆D。
化学仪器维度集合:I={I1,I2,…,Ib},Ii表示第i种化学仪器申请数目,I*为I的子集即I*⊆I。
时间维度集合:T={T1,T2,…,Th},Ti表示第i个时间段。
实验室维度集合:P={P1,P2,…,Pv},Pi表示第i个实验室。
则将求解问题的六维空间的所有集合元素做笛卡尔积S=U×L×D*×I*×T×P,便可得到该问题的求解空间。求解空间中每一个解记为:
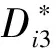
其中max=x*y*z*b*h。
1.2 目标函数的定义
在解空间中不是所有的解都是需要的,也不是所有的解都是最优的[10],因为这些解是要满足一些约束条件[11]。本文将其约束条件定义为过滤准则和优化规则。
(1) 过滤规则(CR)。用户在某一时间不能同时在多个实验室上课;实验室在某一时间不能同时承担多门课。
输入:
∅
规则:
CR=
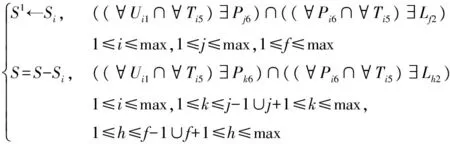
输出:S1。
(2) 优化规则(OR)。用户如果连续更换实验室,那么其距离不要过远;用户不宜连续进行多次试验;实验室、药品和仪器分布尽可能均匀;获得资源的等待时间要尽可能小。优化准则定义为
min(con(Pi,Pj)∩Mean(D,I,P)∩Wait(D,I,P))
定义1(代价距离) 代价距离采用二维特征矩阵表示,假定用户从Pi转移到Pj。
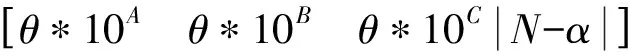
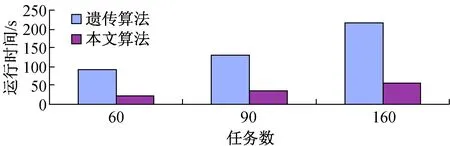
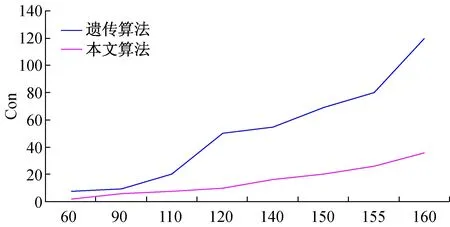
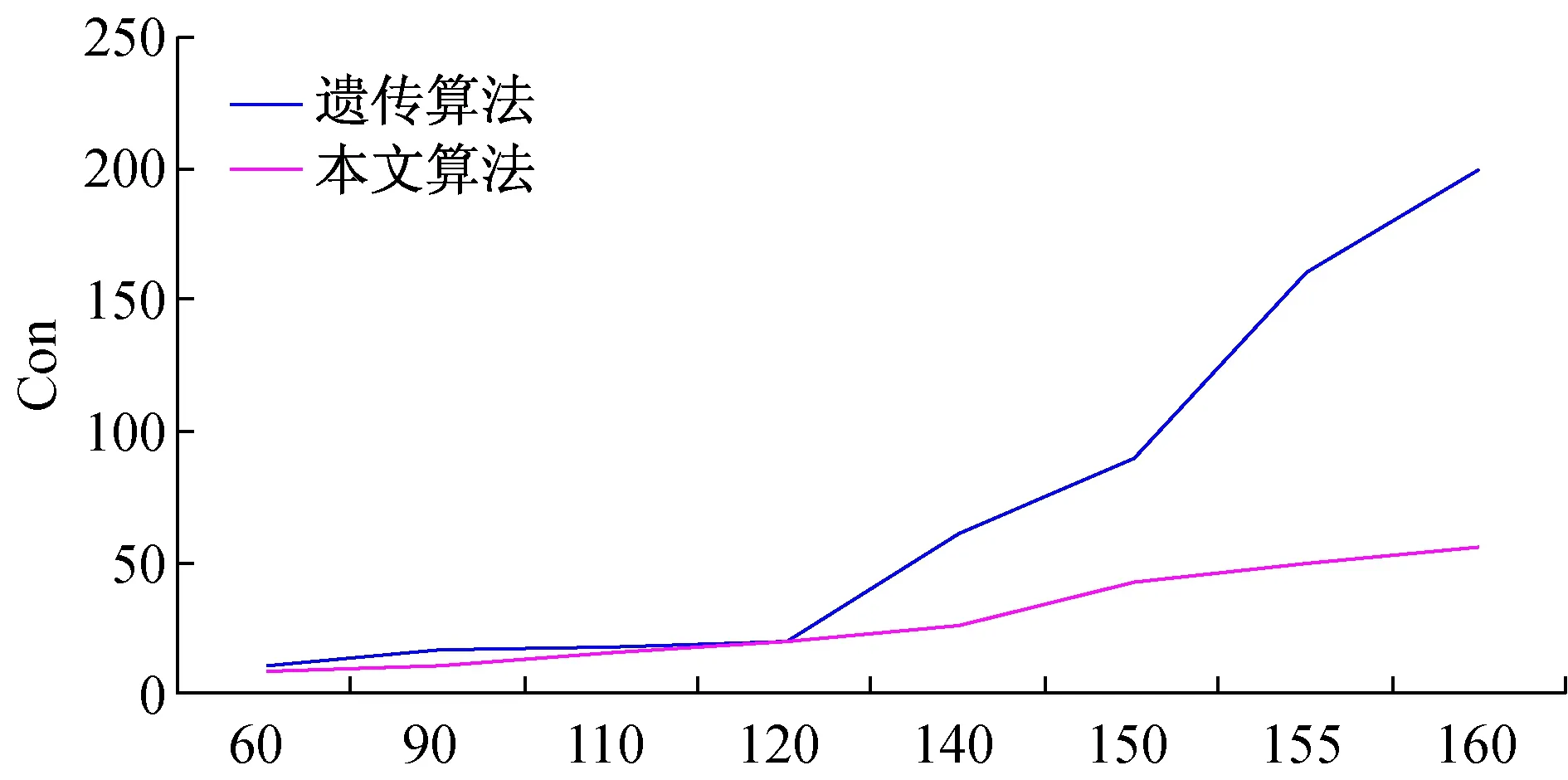
(θ∈(0,1),A 根据特征矩阵可以求出实验室间的距离为 其中:如果在同一个教学楼将其距离级别定义为A;在同一个校区的不同教学楼距离级别定义为B;在不同校区距离级别定义为C;N为Pi所在教学楼楼层最大数;α为Pi所在的楼层数;β为Pj所在楼层数;这里设置A=0,B=1,C=2。代价距离越大,表示连续更换的实验室间距离越远。 定义2(均衡度) 解空间的均衡度为化学药品均衡度、化学仪器均衡度和实验室均衡度之和即 Mean(D,I,P)=Mean(D)+Mean(I)+Mean(P) 均衡度越小说明资源的均匀分布程度越好。 化学药品均衡度定义为: Mean(D)=13(z/x-Num(Ui1)()2+ z/y-Num(Li2)()2+z/h-Num(Ti5)()2) 其中,Num()用于统计D在U,L,T三个维度的每个分量上的总数。 化学仪器均衡度定义为: Mean(I)=13(b/x-Num(Ui1)()2+ b/y-Num(Li2)()2+b/h-Num(Ti5)()2) 其中,Num()用于统计I在U,L,T三个维度的每个分量上的总数。 实验室均衡度定义为: Mean(P)=13(v/x-Num(Ui1)()2+ v/y-Num(Li2)()2+v/h-Num(Ti5)()2) 其中,Num()用于统计P在U,L,T三个维度的每个分量上的总数。 定义3(等待时间) 此处基于马尔可夫排队网络[12]定义等待时间: 每一种资源的等待时间求解如下(以资源的个数为6为例),求解方程为: 方程的解为: 其中,λ,a1,d1,a2,d2由抽样及并行皮尔逊检验法获得。 本文采用粒子群算法[13-15]来求解化学实验室无纸化资源优化配置问题,需将粒子群算法进行实例化。其中Si=(Ui1,Li2,D,i3,Ii4,Ti5,Pi6)表示粒子群算法的第i粒子,适应度函数的定义要参照过滤准则和优化准则,具体定义如下: MIN(Con(Pi,Pj)∩Mean(D,I,P)∩Wait(D,I,P)) s.t.S∈CR 由于粒子算法如不加以改进,容易陷入局部极值,求解性能恶劣。因此本文对粒子群算法进行了改进,改进的思想主要来自于遗传算法变异的思想,通过对那些陷入局部极值的粒子进行变异操作,可以使其跳出局部极值点,从而收敛于全局最优解。 高斯分布是概率论和数理统计中一类重要的分布,高斯变异就是在粒子个体的任意一个分量上加上一个服从高斯分布的随机扰动项。 本文对粒子Si=(Ui1,Li2,D,i3,Ii4,Ti5,Pi6)进行高斯变异,定义如下: (3) 步骤1:对每个粒子的位置、速度和公告板进行初始化。 步骤2:通过式(1)计算每个粒子的适应度值。 步骤3:设置公告板1,公告板1记录粒子经过的最好位置,如果粒子的适应度值优于公告板,则公告板1的值更新为当前粒子的适应度值。 步骤4:设置公告板2,公告板2记录粒子群中粒子经历过的最好位置,如果新的粒子群中存在这样的粒子,它的适应度值优于当前公告板2的值,则公告板2的值更新为当前粒子的适应度值。 步骤5:更新每一个粒子的速度和位置。 步骤6:如果公告板2连续2次迭代过程中没有改变或者变化很小(<β),则转向步骤7;否则转向步骤8。 步骤7:将当前粒子群中最差粒子用公告板2中的最优粒子取代得到了新的粒子群状态,对新粒子群中最优粒子按式(3)进行高斯变异,对变异后的最优粒子和公告板2上的最优粒子比较,取二者最优的替换公告板2。 步骤8:判断是否达到了是否已达到的最大迭代次数MaxIteration或最小准则,若不满足,转向步骤3;否则转向步骤 9。 步骤 9: 算法终止,输出公告板2中粒子和函数值。 这部分仿真实验主要对采用本文算法优化前后资源配置情况的对比分析,化学实验室无纸化资源配置任务数为60、70、80、90、100、110、120、130、140、150、160学时,从资源利用率、资源请求等待时间和资源均衡度三个方面对比如表1所示。 表1 优化前后资源配置对照表 由表1可知,通过本文的优化配置算法可以大大提高资源的利用率和减小申请资源的等待时间。 遗传算法是最成熟以及应用最广泛的寻优算法,这部分仿真实验主要是从优化配置的运行时间、适应度值、代价距离和均衡度这四个方面,和遗传算法[16]进行比较。仿真试验中对于遗传算法的控制参数设定为:种群规模为20,个体串长度为22,杂交概率为0.9,变异概率为0.01,最大遗传代数为100;对于改进的粒子群算法控制参数设定为:种群规模为20,最大迭代次数为50。 化学实验室无纸化资源配置任务数为60、90、160时,两种算法各测20组数据取平均值,得到了平均运行时间见图1,得到了平均适应度值见图2。 图1 运行时间对比 由图1可知,本文算法平均运行时间远远低于遗传算法,这说明了本文算法在对化学实验室无纸化资源优化配置中是快速的。 由图2可知,本文算法的平均适应度值要远远高于遗传算法,适应度函数可知,适应度函数值越低代表越接近最优解。这也说明了本文算法在对化学实验室无纸化资源优化配置中是高效的。 此外任务书数从60离散变化到160学时,针对优化准则中的代价距离和均衡度两参数的对比结果如图3和图4所示。 图3 代价距离对比 图4 均衡度对比 由图3可知,本文算法在进行资源配置时候,会使连续更换实验室的距离很小,优化配置性能远远高于遗传算法。 由图4可知,遗传算法随着任务书的逐渐增大,其均衡度会骤然变大,性能下降。而本文算法在人数很大的情况下,其均衡度依然变化缓慢,说明本文算法性能更优。 在高校化学实验室无纸化资源优化配置问题中,首先进行了数学建模,将该优化问题抽象为一个六维解空间内求最优解的问题,提出了过滤准则和优化准则及其相关定义,定义了适应度函数,采用粒子群算法进行最优解的求解,设计出了基于粒子群的化学实验室无纸化资源优化配置算法。经过仿真实验证明,该算法具有运行速度快,性能高效等优点。该算法具有很高的理论价值和实用价值,具有很高推广空间。 [1] 王 睿.优化实验室资源配置,提高实验室使用效能[J].实验室研究与探索,2011,30(10):400-402. WANG Rui. Optimizing the Configuration of Laboratory Resources and Improving the Efficiency of Laboratory Applications[J]. Research and Exploration in Laboratory, 2011, 30(10): 400-402. [2] 盛苏英,堵 俊,吴 晓.高校实验室信息化管理的研究与实践[J].实验室研究与探索,2012,31(12):184-187. SHENG Su-ying, DU Jun, WU Xiao. Laboratory Information Management in Colleges and Universities[J]. Research and Exploration in Laboratory, 2012, 31(12): 184-187. [3] 董振旗,陈桂明,白志成,等.加强仪器设备管理提高教学保障效能[J].实验室研究与探索,2007,26(1):128-130. DONG Zhen-qi, CHEN Gui-ming, BAI Zhi-cheng,etal. Strengthening the Management of Instrument and Equipment to Enhance the Efficiency of Teaching Support[J]. Research and Exploration in Laboratory, 2007, 26(1) : 128-130. [4] 蔡海燕,刘 昭.实验室信息化管理初探[J].实验室研究与探索,2010,29(9):168-170. CAI Hai-yan, LIU Zhao. Discussion on the Information Management of Laboratory[J]. Research and Exploration in Laboratory, 2010,29(9):168-170. [5] 刘婷婷,张孝良,曹 萍.医药院校实验室资源配置模式的探索[J].实验室研究与探索,2010,29(1):156-158. LIU Ting-ting, ZHANG Xiao-liang, CAO Ping. Exploration on Resources’ Configuration Pattern of Medical Universities[J]. Research and Exploration in Laboratory, 2010, 29(1): 156-158. [6] 马书刚,杨建华.虚拟组织服务资源的优化配置模型[J].计算机工程与应用,2012,48(23):224-229. MA Shu-gang, YANG Jian-hua. Optimal service resource allocation model for virtual organization. Computer Engineering and Applications[J]. Computer Engineering and Applications, 2012, 48(23): 224-229. [7] 尹 呈,郭观七,李文彬,等.基于自适应学习的多目标粒子群优化算法[J].计算机应用研究,2012,29(9):3232-3235. YIN Cheng,GUO Guan-qi,LI Wen-bin,etal. Multi-objective particle swarm optimization algorithm based on self-adaptive learning[J]. Application Research of Computers, 2012, 29(9):3232-3235. [8] 魏国强,景 琳.多应急点资源优化调度模型研究[J].统计与决策,2010(2):10-12. WEI Guo-qiang, JING Ling. Research the Optimization Scheduling Model of Multi-Emergency Resources [J]. Statistics and Decision, 2010(2): 10-12. [9] 胡飞虎,耿泽飞,陈慧敏,等.多资源组合多目标应急调度问题的研究[J].微计算机信息,2009,25(7):9-10. HU Fei-hu, GENG Ze-fei, CHEN Hui-min,etal. Research of Multi-Resource Combinatorial and Multi-Objective Scheduling Problem in Emergency Systems[J]. Microcomputer Information, 2009, 25(7): 9-10. [10] 孙 敏,潘 郁.多资源复杂网络的应急调度研究[J].运筹与管理,2009,18(6):165-169. SUN Min, PAN Yu. Multi-resource Emergency Scheduling Based on Complex-network[J]. Operations Research and Management Science, 2009, 18(6): 165-169. [11] 刘士新.项目优化调度理论与方法[M].北京:机械工业出版社,2006:26-58. [12] 张于贤,于 明,叶冰冰.基于开排队理论的生产线设备资源优化配置[J].系统科学学报,2012,20(3):75-78. ZHANG Yu-xian, YU Ming, YE Bing-bing. Optimum Distribution of Equipment Resources in Production Line Based on Open Queuing Network[J]. Journal of Systems Science, 2012, 20(3): 75-78. [13] 张 凯,赵国荣,姜 静.资源约束项目调度问题的粒子群优化算法求解[J].海军航空工程学院学报,2009,24 (5 ):578 -582. ZHANG Kai, ZHAO Guo-rong, JIANG Jing. Particle Swarm Optimization Algorithm for Resource-Constrained Project Scheduling Problem[J]. Journal of Naval Aeronautical and Astronautical University, 2009, 24 (5): 578-582. [14] 刘军民,高岳林.混沌粒子群优化算法[J].计算机应用,2008,28(2):322-325. LIU Jun-min, GAO Yue-lin. Chaos particle swarm optimization algorithm [J]. Computer Applications, 2008, 28(2): 322-325. [15] 王华秋,曹长修.并行混沌粒子群优化研究及应用[J].计算机仿真,2005,22(11): 98-101. WANG Hua-qiu, CAO Chang- xiu. Research and Application of Parallel Chaos Particle Swarm Optimization[J]. Computer Simulation, 2005, 22(11): 98-101. [16] 崔海波,曾 熠.基于改进遗传算法的资源优化配置研究[J].计算机仿真,2008,25(6):173-176. CUI Hai-bo, ZENG Yi. Scheduling Resources Based on Improved Genetic Algorithm[J]. Computer Simulation, 2008, 25(6): 173-176. 把改革创新作为教育发展的强大动力。教育要发展,根本靠改革。要以体制机制改革为重点,鼓励地方和学校大胆探索和试验,加快重要领域和关键环节改革步伐。创新人才培养体制、办学体制、教育管理体制,改革质量评价和考试招生制度,改革教学内容、方法、手段,建设现代学校制度。加快解决经济社会发展对高质量多样化人才需要与教育培养能力不足的矛盾、人民群众期盼良好教育与资源相对短缺的矛盾、增强教育活力与体制机制约束的矛盾,为教育事业持续健康发展提供强大动力。 ——摘自《国家中长期教育改革和发展规划纲要》
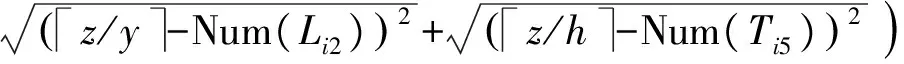

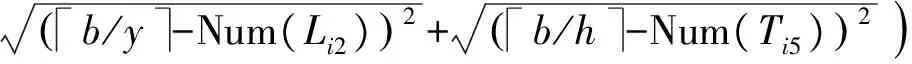
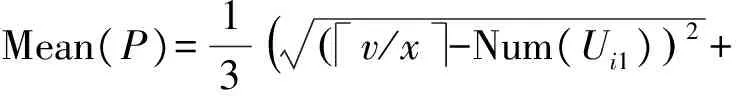

2 基于改进粒子群的问题求解算法
2.1 模型的实例化
2.2 粒子群的改进
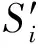
2.3 算法的实现
3 仿真实验分析
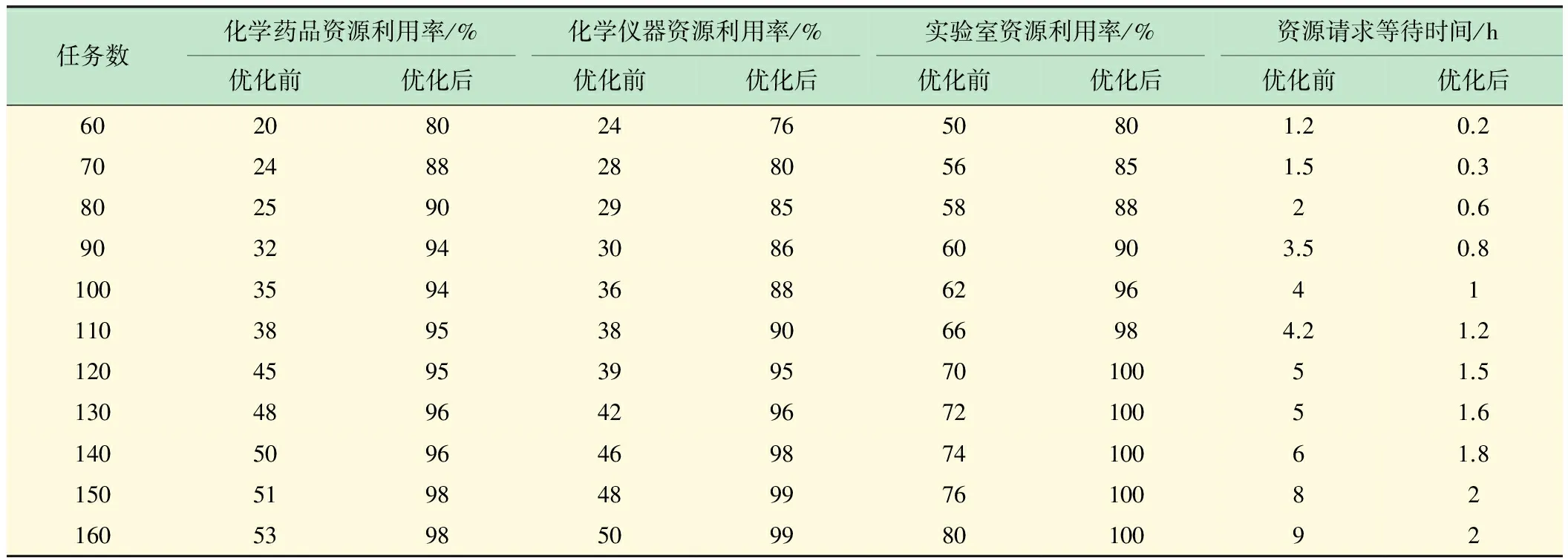
3.1 优化前后实验分析
3.2 性能对比分析
4 结 语

