2阶微分方程的解与小函数的关系

闵小花，张红霞，易才凤

(江西师范大学数学与信息科学学院，江西南昌330022)

0 引言与结果

本文使用Nevanlinna值分布理论的标准记号［1-2］，用 σ(f)表示亚纯函数 f(z)的增长级，λ(f)表示f(z)的零点收敛指数表示f(z)的不同零点收敛指数表示f(z)取小函数φ的不同点的收敛指数，σ2(f)表示亚纯函数f(z)的超级，表示f(z)取小函数φ的不同点的2级收敛指数.

关于微分方程的解与小函数的关系已被众多学者研究，得到了一些有趣的结果［3-6］.例如关于2阶线性微分方程

陈宗煊在文献［7］中证明了下面的结果.

定理A 假设Aj(z)≢0(j=0，1)是整函数，σ(Aj)＜ 1，a，b是复常数且满足ab≠0和a≠b，则方程(1)的每个解f(≢0)都具有无穷级.

之后，陈宗煊等在文献［3］中又研究了方程(1)的解及其导数与小函数之间的关系，证明了下面2个定理.

定理B 假设Aj(z)≢0(j=0，1)是整函数，σ(Aj)＜ 1，a，b是复常数且满足ab≠0和a≠b，如果φ(z)(≢0)是有限级整函数，则方程(1)的每个解f(≢0)满足

定理C 假设Aj(z)≢0(j=0，1)是整函数，σ(Aj)＜1，a，b是复常数且满足ab≠0和arg a≠arg b或a=cb(0＜c＜1)，如果φ(z)(≢0)是有限级整函数，则方程(1)的每个解f(≢0)满足

另外，关于2阶线性微分方程

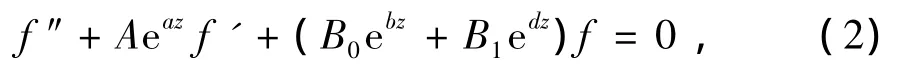
文献［8］证明了下面的结果.

定理D 假设A(z)(≢0)，Bi(z)(≢0)(i=0，1)是整函数，σ(A)＜1，σ(Bi)＜1，a，b，d 是复常数且(a-b)(ad)≠ 0，当 b=d时，B0(z)+B1(z)≢ 0，如果φ(z)(≢0)是级小于1的整函数，则方程(2)的每个解f(≢0)满足

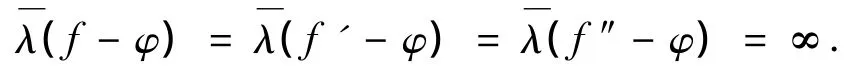
以上定理研究了方程(1)和(2)的解及其导数取小函数的不同点的收敛指数与解的增长级之间的关系，证明了方程(1)和(2)的解f(≢0)满足.本文是在前人研究的基础上，进一步研究了方程(1)和(2)以及相关的非齐次方程的解及其导数取小函数的不同点的2级收敛指数与解的超级之间的关系，得到了下面的结果.

定理1 假设Aj(z)≢0(j=0，1)是整函数，σ(Aj)＜1，a，b是复常数且满足ab≠0和a≠b，如果φ(z)(≢0)是有限级整函数，则方程(1)的每个解f(≢0)满足进一步，如果φ(z)(≢0)是级小于1的整函数，则方程(1)的每个解f(≢0)还满足且

定理2 假设Aj(z)≢0(j=0，1)是整函数，σ(Aj)＜ 1，a，b是复常数且满足ab≠0和a≠b，如果φ(z)(≢0)，F(z)(≢0)都是有限级整函数，则方程

定理3 假设Aj(z)≢0(j=0，1)是整函数，σ(Aj)＜1，a，b是复常数且满足ab≠0和arg a≠arg b或a=cb(0＜c＜1)，如果φ(z)(≢0)是有限级整函数，则方程(1)的每个解 f(≢0)满足

定理4 假设A(z)(≢0)，Bi(z)(≢0)(i=0，1)是整函数，σ(A)＜1，σ(Bi)＜1，a，b，d 是复常数且(a-b)(ad)≠ 0，当 b=d时，B0(z)+B1(z)≢ 0，如果φ(z)(≢0)是级小于1的整函数，则方程(2)的每个解f(≢0)满足

定理5 假设A(z)(≢0)，Bi(z)(≢0)(i=0，1)是整函数，σ(A)＜1，σ(Bi)＜1，a，b，d 是复常数且(a-b)(ad)≠ 0，当 b=d时，B0(z)+B1(z)≢ 0，如果φ(z)(≢0)和F(z)(≢0)都是级小于1的整函数，则方程

1 引理

引理1［9］假设aj(j=0，1，…，k-1)，F(≢0)是整函数，f满足微分方程

且max{σ(F)，σ(aj);j=0，1，…，k-1}＜ σ(f)=σ(0＜σ≤∞)，则

注1 由引理1的证明过程易知，当aj(j=0，1，…，k-1)和F是亚纯函数时，引理1的结论也成立.

引理2 在引理1的条件下，若σ(f)=∞，则在引理1的结论下，进一步还有

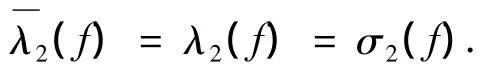
证将(4)式改写为

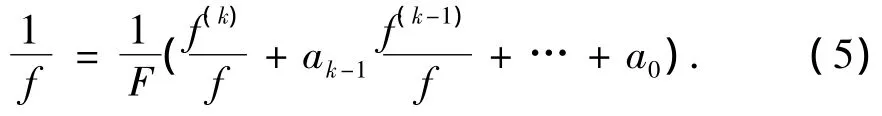
由(5)式，若z0为f的大于k的α阶零点，则z0必为F的α-k阶零点，从而有

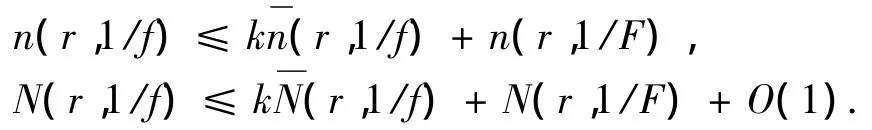
再由对数导数引理，至多除去1个线测度为有限的r值集E外，有

所以

因为max{σ(F)，σ(aj);j=0，1，…，k-1}＜σ(f)=∞，所以由上式可得).故有

引理3［10］假设f1(z)，f2(z)，…，fn(z)(n≥2)为亚纯函数，g1(z)，g2(z)，…，gn(z)为整函数，满足条件

(ii)gj(z)-gk(z)(1≤j＜k≤n)不为常数;

(iii)T(r，fj)=o［T(r，egh-gk)］(1≤j≤n，1≤h＜k≤n)(r→∞，r∉E)，其中E是对数测度为有限的集合，

则有 fj(z)≡0(j=1，2，…，n).

由定理A容易得到下面的引理4.

引理4 假设Aj(z)≢0(j=0，1)是整函数，σ(Aj)＜ 1，a，b是复常数且满足ab≠0和a≠b，如果F(≢0)是有限级整函数，则方程(3)的每个解f(≢0)的级为无穷，至多除去1个例外的非零解.

引理5［3］假设a，b是复常数满足ab≠0和arg a≠arg b或a=cb(0＜c＜1)，定义指标集:Λ1={0，a};Λ2={0，a，b，a+b，2a}.

(i)如果Hj(j∈Λ1)和Hb都是级小于1的亚纯函数，则

(ii)如果Hj(j∈Λ2)和H2b都是级小于1的亚纯函数，则ψ2(z)+H2be2bz≢0;

(iii)假设 ψ20(z)，ψ21(z)，ψ22(z)具有(ii)中ψ2(z)的形式，H2b(z)≢0，φ(z)是有限级亚纯函数，则

引理6［11］假设A(z)，Bi(z)(i=0，1)是整函数，σ(A)＜ 1，σ(Bi)＜ 1，且则方程(2)的每个解f(≢0)的级为无穷.

注2 从引理6的证明过程可以知道A(z)≢0，Bi(z)≢0(i=0，1)且 abd≠0.

2 定理的证明

定理1 的证明假设f(≢0)是方程(1)的解，则f是整函数，由定理A可知σ(f)=∞.令g0(z)=f(z)-φ(z)，则σ(g0)=σ(f)=∞，再由定理B知，进一步有.将f=g0+φ代入(1)式，得到

注意到(6)式可能存在有限级解，但这里可仅讨论满足g0=f-φ的无穷级解，所以只需对(6)式的无穷级整函数解g0证明成立.

由于方程(1)的所有非零解为无穷级而φ(z)是有限级整函数，可知

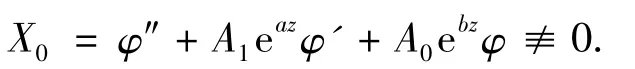
又因σ(X0)＜σ(g0)=∞，σ(A0eaz)=σ(A1ebz)=1＜σ(g0)=∞，对方程(6)应用引理2有λ2(g0)= σ2(g0)，即

令g1=f'-φ，则σ(g1)= σ(f')= σ(f)=∞，并且

对方程(1)两边进行微分，得到

由(1)式得到

将(8)式代入(7)式得

将f'=g1+ φ，f″=g'1+ φ'，f‴=g″1+ φ″代入(9)式，得到

其中h1=A1eaz-(A0ebz)'(A0ebz)，h0=(A1eaz)'+A0ebz-(A0ebz)'A1eaz(A0ebz)，-h= φ″+(A1eaz-(A0ebz)'(A0ebz))φ'+ ［(A1eaz)'+A0ebz-(A0ebz)'A1eaz(A0ebz)］φ= φ″-(A'0/A0+b)φ'+［A1φ'+A'1φ +A1aφ -(A'0/A0+b)A1φ］eaz+A0φebz.

现证明h≢0.事实上，如果h≡0，则

由引理3可知A0≡0，这与题设矛盾，所以h≢0.

将(8)式代入(11)式，并由(9)式得到

其中

显然 H3，H2，U1，U2都是亚纯函数，并且它们的级都小于或等于1.

将f″=g2+ φ，f‴=g'2+ φ'，f(4)=g″2+ φ″代入(12)式，得到

记X= φ″+H3φ'+H2φ，使用类似于上面的证明方法，可得X≢0.

定理2 的证明假设f(≢0)是方程(3)的解，则f是整函数，由引理4可知，至多除去1个例外的非零解，其他所有非零解满足σ(f)=∞.令g3(z)=f(z)-φ(z)，由σ(φ)＜∞ 知σ(g3)= σ(f)=∞，且有和.将f=g3+φ代入(3)式，得到

记 X1=F-{φ″+A1eazφ'+A0ebzφ}=F-X0，显然X1≢0.若不然，则φ是方程(3)的解，故由引理4可知，至多除去1个例外的非零解φ(z)，其它所有的φ是无穷级，这与φ的假设矛盾.

下证进一步的结论.

对方程(3)两边进行微分，得到

由方程(3)得到

将(16)式代入(15)式得

将f'=g4+ φ，f″=g'4+ φ'，f‴=g″4+ φ″代入(17)式，得到 g″4+h1g'4+h0g4=h2，其中

现证明h2≢0.事实上，如果h2≡0，则

将上式两边乘以A0ebz，得到

因为σ(Aj)＜ 1(j=0，1)，σ(F)＜ 1，σ(φ)＜1，由引理3有A20≡0，即A0≡0，与题设矛盾，故h2≢0.

微分(15)式的两边，得到

将(16)式代入(18)式，并由(17)式得到

其中

显然 H3，H2，H1，U1，U2都是亚纯函数，且它们的级都小于或等于1.

将f″=g5+ φ，f‴=g'5+ φ'，f(4)=g″5+ φ″代入(19)式，得到

g″5+H3g'5+H2g5=H1-(φ″+H3φ'+H2φ).

记 X2=H1-(φ″+H3φ'+H2φ)，使用类似于上面的证明方法，可得X2≢0.

定理3 的证明假设f(≢0)是方程(1)的解，则f是整函数，由定理A可知σ(f)=∞.又由定理C知，再由定理3的条件满足定理1的条件，所以有

现证明h≢0.事实上，如果h≡0，则

由引理5中(iii)，可得

这个矛盾表明h≢0.

记 X= φ″+H3φ'+H2φ，使用类似于上面的证明方法，可得X≢0.

定理4 的证明假设f(≢0)是方程(2)的解，则f是整函数，由引理6可知σ(f)=∞.令g0(z)=f(z)-φ(z)，则σ(g0)=σ(f)=∞，再由定理D可知，还有

将f=g0+φ代入(2)式，得到

注意到(20)式可能存在有限级解，但这里仅需讨论满足g0=f-φ的无穷级解，所以只需对(20)式的无穷级整函数解g0证明即可.

由于方程(2)的所有非零解具有无穷级而φ(z)(≢0)是有限级整函数，可知

X0= φ″+Aeazφ'+(B0ebz+B1edz)φ ≢0，从而，由引理2可得，即

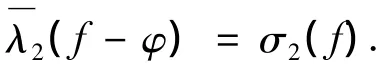
对方程(2)两边进行微分，得到

由方程(2)有

将(22)式代入(21)式得

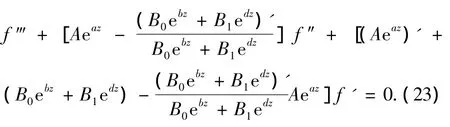
将f'=g1+ φ，f″=g'1+ φ'，f‴=g″1+ φ″代入(23)式，得到 g″1+h1g'1+h0g1=h，其中

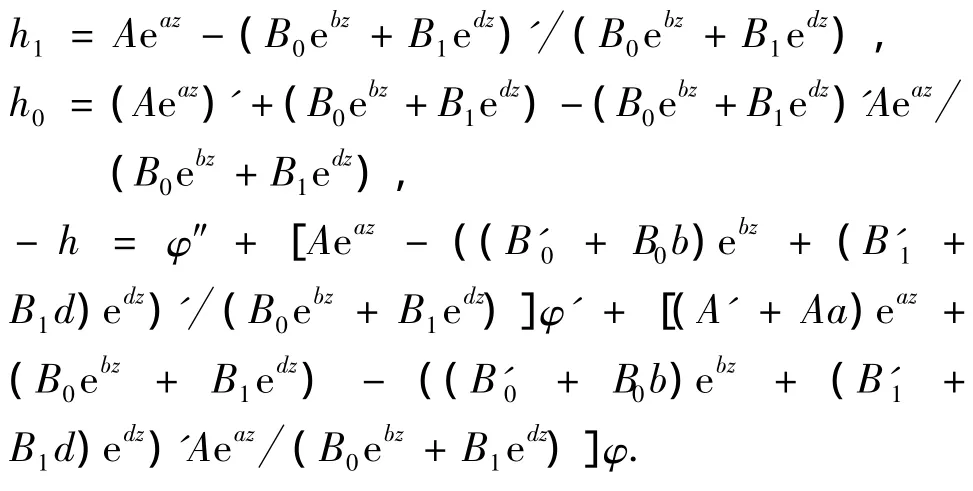
现证明h≢0.事实上，如果h≡0，则

下面分2种情形讨论:

由于A，B0，B1，φ的增长级都小于1，由引理3可知(B0+B1)2≡0，这与题设矛盾.

情形2 当b≠d时，由条件(a-b)(a-d)≠0知a≠b且a≠d，再对(24)式应用引理3得2B0B1≡0，这也与题设矛盾.

令 g2=f″- φ，则 σ(g2)= σ(f″)= σ(f)=∞和

微分(21)式，可得

将(22)式代入(25)式，并由(23)式得到

其中

显然 H3，H2，U1，U2都是亚纯函数，且它们的增长级都小于或等于1.

将f″=g2+ φ，f‴=g'2+ φ'，f(4)=g2″+ φ″代入(26)式，得到

使用类似于上面的证明方法，可得X1=φ″+因此，由引理 2可得σ2(g2)，即

定理5 的证明由引理6，用类似于定理2 ，定理3及定理4的证明方法可证得定理5也成立.

［1］Hayman W K.Meromorphic function［M］.Oxford:Clarendon Press，1964.

［2］杨乐.值分布论及其新研究［M］.北京:科学出版社，1982.

［3］陈宗煊，孙光镐.一类二阶微分方程的解和小函数的关系［J］.数学年刊:A 辑，2006，27(4):431-442.

［4］陈裕先，陈宗煊.微分方程的解与小函数的关系［J］.江西师范大学学报:自然科学版，2002，26(1):15-20.

［5］程涛，陈宗煊.非齐次线性微分方程解取小函数的点的收敛指数［J］.江西师范大学学报:自然科学版，2002，26(1):21-27.

［6］刘慧芳.齐次线性微分方程解取小函数的点的收敛指数［J］.江西师范大学学报:自然科学版，2003，27(2):118-121.

［7］陈宗煊.微分方程f″+e-zf'+Q(z)f=0解的增长性［J］.中国科学:A 辑，2001，31(9):775-785.

［8］安蕾，肖丽鹏.一类2阶微分方程的解和小函数的关系［J］.江西师范大学学报:自然科学版，2013，37(3):233-235.

［9］Chen Zongxuan.Zeros ofmeromorphic solutions of higher order linear differential equations［J］.Analysis，1994，14(4):425-438.

［10］Yang Congjun，Yi Hongxun.Uniqueness theory ofmeromorphic functions［M］.New York:KluwerAcademic Publishers，2003.

［11］Cheng Tao，Kang Yueming.The growth of the solutions of a certain linear differential equation［J］.Journal of FudanUniversity，2006，45(5):611-618.