伪补MS-代数的核理想与同余关系

赵秀兰，刘 洁

(黄河科技学院数理部，河南郑州450063)

0 引言

1个伪补代数(简称p-代数)指的是1个代数(L;∨，∧，*)，L具有1个最小元0及1个映射*:.p-代数的基本性质请参见文献［1-3］.文献［4］在德摩根代数和Stone代数的基础上抽象出MS-代数，MS-代数是指1个有界配格被赋予1个1元运算x→x°使得x≤x°°且有(x∧y)°=x°∨y°，1°=0.方捷［5］在p-代数与MS-代数的基础上引入1类新的代数，称为伪补 MS-代数(L;∨，∧，*，°，0，1)(简称 pMS-代数).pMS-代数指的是1个有界分配格，被赋予2个1元运算*和°，即(L;*)是1个p-代数，(L;°)是1个MS-代数，且运算*和°满足交换律.文献［5］从pMS-代数的运算属性，同余关系及其次直不可约代数的角度研究了代数的结构.

理想是研究代数结构的一个重要工具.目前，有些学者借助理想已经刻画了部分代数的结构.如文献［6］研究了伪补Ockham代数上的理想与滤子，构造出了具有核理想与余核滤子的最小同余关系和最大同余关系.2007年，方捷等［7］刻画了平衡拟补Ockham代数的理想格的性质，将理想格构造成了一个伪补代数.王雷波等［8］研究了双重伪补代数的假值理想和假值同余.文献［9］研究了双重伪补Ockham代数上的理想与滤子的性质，结论是双重伪补Ockham代数上的理想格与其滤子格同构.文献［10］对于BR0代数中的*理想及其诱导的商代数给出了特征刻画.在此研究工作的基础上，本文主要讨论pMS-代数的理想格及核理想的性质与特征，并刻画由pMS-代数的核理想生成的同余关系.

设I是格L的子格，如果x，y∈L，y≤x∈I总有y∈I，则称子格I是格L的理想.对于L的理想I，若存在L的1个同余关系φ使得I=Kerφ，其中Kerφ=，称理想I为L的核理想.假定L是pMS-代数，设θ是L的1个格同余，且∀a，b∈L，(a，b)∈ θ蕴涵(a*，b*)∈ θ及(a°，b°)∈θ，则称θ是L的1个同余.设a，b是L中的元素，又F是L的1个子集.将用符号θ(a，b)和θlat(a，b)分别表示由a，b所生成的主同余和格主同余;用θ(F)和θlat(F)分别表示由F所生成的主同余和格主同余;符号ConL表示L的所有同余所组成的同余格.

1 核理想的性质

核理想是1类特殊的理想［11］，理想若要转化为核理想，在pMS-代数中需有如下性质.

定理1 设(L;∨，∧，*，°，0，1)是1个 pMS-代数，I是L的理想，则I是L的核理想，当且仅当(a∈L)a∈I⇒{a＊＊，a*°}⊆I.

证充分性设I是L的核理想，则∃φ∈ConL 使得I=Kerφ.令 a ∈I，则有 a ≡0(φ)，从而a＊＊≡0(φ)，a*°≡0(φ)，于是由核理想的定义知{a＊＊，a*°}⊆I.

必要性设∀a∈L，a∈I蕴涵a＊＊，a*°∈I.在L上定义等价关系RI如下:

(x，y)∈ RI⇔(∃i∈I)x∨i=y∨i.易见，RI是1个格同余.

下证RI∈ConL.事实上，若(x，y)∈ RI，则∃i∈I使得x∨i=y∨i.从而有x*∧i*=y*∧i*，故(x*∧i*)∨i＊＊=(y*∧i*)∨i＊＊.即(x*∨i＊＊)∧(i*∨i＊＊)=(y*∨i＊＊)∧(i*∨i＊＊).

由文献［2］知i*∨i＊＊=1，因此，x*∨i＊＊=y*∨i＊＊.又由已知得i＊＊∈I，所以(x*，y*)∈RI.

另一方面，由x∨i=y∨i得x°∧i°=y°∧i°.故有(x°∧i°)∨i*°=(y°∧i°)∨i*°，从而得(x°∨i*°)∧(i°∨i*°)=(y°∨i*°)∧(i°∨i*°).

由文献［5］知 i°=i＊＊°，于是得 i°∨i*°=i＊＊°∨i*°=(i＊＊∧i*)°=0°=1，故x°∨i*°=y°∨i*°.又由已知得 i*°∈I，因此(x°，y°)∈ RI.所以RI∈ConL.

下证KerRI=I.若x∈KerRI，即(x，0)∈RI，则∃i∈I使得 x∨i=i.从而 x≤i∈I，故 x∈I，因此KerRI⊆I.

另一方面，设i∈I，由已知得i＊＊∈I.又由文献［2］知 i≤i＊＊，故 i∈ KerRI，从而有I⊆ KerRI.所以KerRI=I.

由定理1知，RI是具有核理想I的1个同余关系.同时，RI具有下面的性质.

推论1 RI是具有核理想I的最小同余关系.

证由定理1的证明过程知，RI是具有核理想I的同余关系.设φ∈ConL且具有核理想I，即I=Kerφ.∀i∈I有 i≡0(φ).若(x，y)∈ RI，则 ∃i∈I使得x∨i=y∨i.于是得x≡x∨i(φ)，y≡y∨i(φ)，从而有(x，y)∈ φ，所以 RI≤φ.

设(L;∨，∧，*，°，0，1)是 1 个 pMS-代数，记I(L)，KI(L)分别为L的所有理想与所有核理想构成的集合.

定理2 设(L;∨，∧，*，°，0，1)是1个 pMS-代数，则KI(L)是I(L)的子格.

证若I，J∈ KI(L)，易得I∧J∈ KI(L).

下证I∨J∈KI(L).令x∈I∨J，由文献［3］知，∃i∈I及j∈J使得x≤i∨j.从而由文献［5］知x＊＊≤i＊＊∨j＊＊，x*°≤i*°∨j*°.又因为I，J∈KI(L)，根据定理 1 知 i＊＊∈I，i*°∈I，j＊＊∈ J，j*°∈J.所以x＊＊，x*°∈I∨J.又由定理1得I∨J∈KI(L).因此KI(L)是I(L)的子格.

定理3 设(L;∨，∧，*，°，0，1)是1个 pMS-代数，令，其中RI如定理1中定义，则C*(KI(L))是ConL的子格.

证易得R{0}=ω(相等关系)及RL=ι(泛同余关系).

先证 ∀I，J ∈ KI(L)，有 RI∧RJ=RI∧J.

由定理2 知I∧J∈KI(L).设(x，y)∈RI∧RJ，由文献［3］知(x，y)∈RI且(x，y)∈RJ.因此∃i∈I，j∈ J使得 x∨i=y∨i，x∨j=y∨j，从而有x∨(i∧j)=y∨(i∧j).又因为i∧j∈I∧J，所以(x，y)∈ RI∧J.故 RI∧RJ≤RI∧J.

另一方面，设(x，y)∈ RI∧J，则 ∃i∈I∧J使得x∨i=y∨i，又因为i∈I且i∈J.于是得(x，y)∈RI，(x，y)∈ RJ，因此(x，y)∈ RI∧RJ，从而 RI∧J≤RI∧RJ.所以 RI∧RJ=RI∧J.

下证 ∀I，J ∈ KI(L)，有 RI∨RJ=RI∨J.

由定理2 知I∨J∈KI(L).设(x，y)∈RI∨J，则∃h∈I∨J有 x∨h=y∨h.由文献［3］知，∃i∈I，i∈J使得h≤i∨j.于是得x∨i∨j=y∨i∨j，所以有

因此(x，y)∈ RI∨RJ，从而有 RI∨J≤RI∨RJ.

另一方面，设(x，y)∈ RI∨RJ，则 ∃x=x0，x1，…，xn-1=y且(xi，xi+1)∈ RI或者(xi，xi+1)∈ RJ.不失一般性，假设 x=x0≡RIx1≡RJx2≡RIx3≡ … ≡ xn-1=y，则 ∃i1，i2，…，it∈I，j1，j2，…，js∈ J，使得

x∨i1=x1∨i1，x1∨j1=x2∨j1，x2∨i2=

x3∨i2，….

令i=i1∨i2∨…∨it∨j1∨j2∨…∨js，显然有i∈I∨J.因此x∨i=x1∨i= …=y∨i，即(x，y)∈ RI∨J.故 RI∨RJ≤RI∨J.

2 核理想的同余关系

定理4 设(L;∨，∧，*，°，0，1)是pMS-代数，I是L的核理想，则θ(I)=θlat(I)∨θlat(Io).

证设a，b∈L且a≤b，易得a*，b*∈Io.由定理1知a°*，b°*∈I.又由文献［5］知，a°=a°＊＊，b°=b°＊＊，从而有 a°，b°∈Io. 所以 θlat(a，b)≤θlat(I)，θlat(b°，a°)≤θlat(Io)，θlat(b*，a*)≤θlat(Io).由文献［5］知，若L∈pMS，a，b∈L且a≤b有θ(a，b)= θlat(a，b)∨θlat(b°，a°)∨θlat(b*，a*).所以 θ(a，b)≤θlat(I)∨θlat(Io).由文献［3］知，于是可得 θ(I)≤θlat(I)∨θlat(Io).

另一方面，设a，b∈Io，a≤b，由Io的定义知，∃c∈I使得b≥a≥c*.由于(0，c)∈θ(I)，因此(c*，1)∈ θ(I).又因为(a，a)，(b，b)∈ θ(I)，故(a∨c*，a∨1)∈θ(I)，(b∨c*，b∨1)∈θ(I)，即(a，1)∈ θ(I)，(b，1)∈ θ(I)，从而得(a，b)∈θ(I).结合，故有θ(Io)≤θ(I)，所以 θlat(I)∨θlat(Io)≤θ(I).

定理5 设(L;∨，∧，*，°，0，1)是pMS-代数，I是L的核理想，则

(x，y)∈ θ(I)⇔(∃a，b∈I)(x∨a)∧b*=

(y∨a)∧b*.

证在L上定义1个等价关系φ如下:

(x，y)∈ φ⇔(∃a，b∈I)(x∨a)∧b*=

(y∨a)∧b*.

易见，φ是1个格同余.

先证φ∈ConL.设(x，y)∈φ，则∃a，b∈I使得(x∨a)∧b*=(y∨a)∧b*.故

(x°∧a°)∨b*°=(y°∧a°)∨b*°，从而有(x°∨b*°)∧(a°∨b*°)=(y°∨b*°)∧(a°∨b*°).

又因为a°∨b*°≥a°，于是(x°∨b*°)∧a°=(y°∨b*°)∧a°.由文献［5］知 a°=a°＊＊=(a°*)*，故(x°∨b*°)∧(a°*)*=(y°∨b*°)∧(a°*)*.由定理1 知 b*°，a°*∈I，故(x°，y°)∈ φ.

另一方面，由(x∨a)∧b*=(y∨a)∧b*得(x*∧a*)∨b＊＊=(y*∧a*)∨b＊＊，即

(x*∨b＊＊)∧(a∧b*)*=(y*∨b＊＊)∧

(a∧b*)*.

又由定理1知b＊＊∈I且a∧b*≤a∈I，故由φ的定义得(x*，y*)∈φ.因此φ∈ConL.

下证φ= θ(I).设(x，y)∈φ，则∃a，b∈I使得(x∨a)∧b*=(y∨a)∧b*.因为(a，0)∈θlat(I)，(b*，1)∈ θlat(Io)，所以(x，x∨a)∈θlat(I)，((x∨a)∧b*，x∨a)∈ θlat(Io)，因此

(x，(x∨a)∧b*)∈ θlat(I)∨θlat(Io).

同理可得(y，(y∨a)∧b*)∈ θlat(I)∨θlat(Io).所以(x，y)∈ θlat(I)∨θlat(Io)，即 φ≤θlat(I)∨θlat(Io)，结合定理4知φ≤θ(I).

另一方面，设(x，y)∈ θ(I)= θlat(I)∨θlat(Io)，则 ∃x=x0，x1，…，xn-1=y 且(xi，xi+1)∈θlat(I)或者(xi，xi+1)∈ θlat(Io)(i=0，1，2，…，n-2).不失一般性，假设

则 ∃i1，i2，…，it∈I，j1，j2，…，js∈I，使得x∨i1=x1∨i1，x1∧j1*=x2∧j1*，x2∨i2=x3∨i2，x3∧j2*=x4∧j2*，….

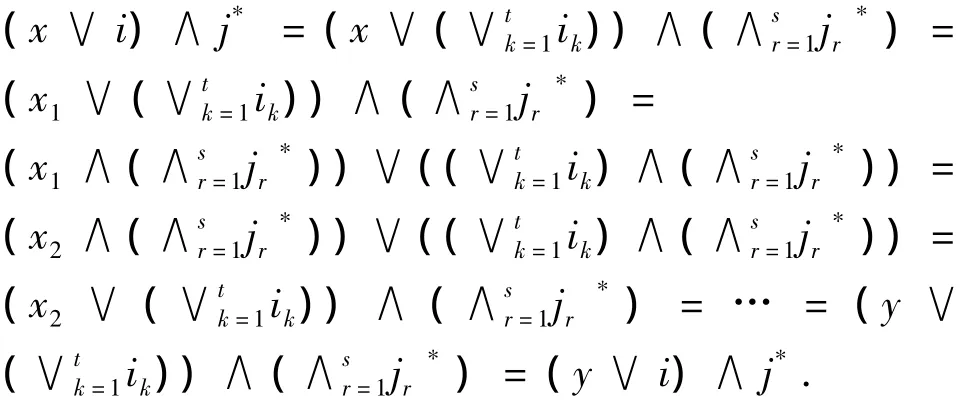
因此(x，y)∈ φ，故 θ(I)≤φ.

推论2 设(L;∨，∧，*，°，0，1)是pMS-代数，I是L的核理想，x，y∈L，则下列命题等价:

(i)(x，y)∈ θ(I);

(ii)(∃i∈I)x∨i=y∨i;

(iii)(∃i，j∈I)(x∨i)∧j*=(y∨i)∧j*.

证显然有(ii)⇒(iii).

由定理5知，(i)⇔(iii).

只需证(iii)⇒(ii).设∃i，j∈I使得(x∨i)∧j*=(y∨i)∧j*.因此((x∨i)∧j*)∨j＊＊=((y∨i)∧j*)∨j＊＊，即 x∨(i∨j＊＊)=y∨(i∨j＊＊).又由定理1知j＊＊∈I，i∈I，故i∨j＊＊∈I，于是(ii)得证.

3 结论

本文将核理想的概念引入到伪补MS-代数上，通过构造具有核理想的同余关系，利用伪补MS-代数主同余表示定理，获得了理想成为核理想的充要条件以及核理想所生成的同余关系的代数表达式.所得结果丰富了格序代数理论［12］.

［1］ Blyth T S，Varlet J C.Ockham algebras［M］.Oxford:OxfordUniversity Press，1994.

［2］ Blyth T S，Fang Jie，Varlet J C.Ockham algebras with pseudocomplementation ［J］.Communications inAlgebra，1997，25(11):3605-3615.

［3］Gratzer G.Lattice theory［M］.New York:W H Freeman Company，1971.

［4］Blyth T S，Varlet J C.On a common abstraction of de Morgan algebras and Stone algebras［J］.Proc Roy Soc Edinburgh，1983，94(3/4):301-308.

［5］Fang Jie.Pseudocomplemented MS-algebras［J］.Algebra Colloq，1996，3(1):59-65.

［6］方捷，吴丽云.拟补Ockham代数的理想与滤子［J］.数学学报，2004，47(4):647-652.

［7］赵秀兰，方捷.平衡拟补Ockham代数的理想格［J］.华南师范大学学报:自然科学版，2007(2):42-47.

［8］王雷波，方捷.双重伪补代数的假值理想的一点注记［J］.纯粹数学与应用数学，2012，28(1):119-122.

［9］赵秀兰，孙中举.双重伪补Ockham代数的理想与滤子［J］.模糊系统与数学，2012，26(3):70-76.

［10］牛超群，吴洪博.BR0代数中的*理想及其诱导的商代数［J］.江西师范大学学报:自然科学版，2013，37(3):221-224.

［11］罗永贵，徐波，高荣海.半群CPOn的每个星理想的秩和相关秩［J］.西南大学学报:自然科学版，2013，35(8):77-82.

［12］纪培胜，綦伟青.原子CSL代数中的Lie理想［J］.广西师范大学学报:自然科学版，2007，25(3):36-39.