一类非线性分数阶微分方程反周期边值问题解的存在性

谢志勇，谢显华，马 丽

(赣南师范学院数学与计算机科学学院，江西赣州341000)

0 引言

分数阶常微分方程是经典的整数阶常微分方程的推广，它是将整数阶的导数用分数阶导数来替换.而与整数阶微分方程相比，分数阶微分方程的优势在于它能更好地模拟自然界的物理过程和动态系统过程.近年来，分数阶微分方程已作为一个重要的研究领域，它将经典微分方程推广到任意阶的情形.现在分数阶微分方程在电子控制、多孔介质等许多领域上都有应用.关于分数阶微分方程解的存在唯一性问题、一些特殊分数阶微分方程解的性态问题、分数阶微分方程数值解的研究参见文献［1-16］.

反周期边值问题理论广泛应用于描述波动环境中物理现象的演化.许多学者关注于分数阶微分方程反周期边值问题解的存在性和唯一性问题.文献［6］考虑了分数阶微分方程反周期边值问题:

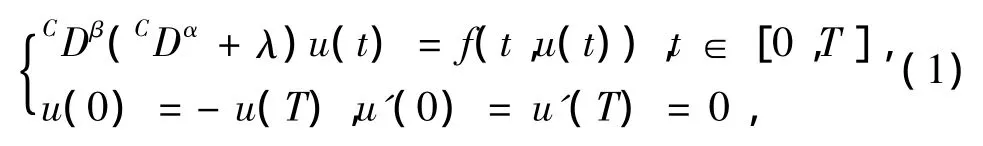
其中CDq表示q阶Caputo分数阶导数，f是给定的连续函数.研究结果主要是基于标准不动点原理得出的.除此之外，文献［7］研究了分数阶微分方程反周期边值问题:

其中CDα表示α阶Caputo分数阶导数，T是1个正的常数，1＜ α≤2，0＜ p，q＜ 1，α -q≥1和f是1个给定的连续函数.

方程(1)中，如果f不仅是t，u(t)的函数，而且也是CDqu(t)的函数，那么方程所描述的物理现象将更普遍.一个自然的问题就是其解的存在唯一性是否能够成立呢?本文将考虑如下分数阶微分方程反周期边值问题解的存在性和唯一性:

其中CDβ表示β阶Caputo分数阶导数，T是1个正的常数，1＜ α≤2，0＜ β≤1，0＜ q＜ 1，α -q≥1，f是1个给定的连续函数和λ是实数.

1 预备知识

本节将给出一些用到的基本概念、记号、定义和已有结果.

定义1 函数f:［0，∞)→R的α阶Caputo分数阶导数定义为

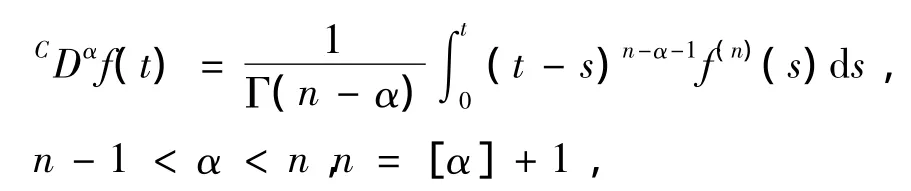
其中［α］表示α的整数部分.

定义2 函数f(t)，t＞0的Riemann-Liouville α阶(α＞0)分数阶积分定义为

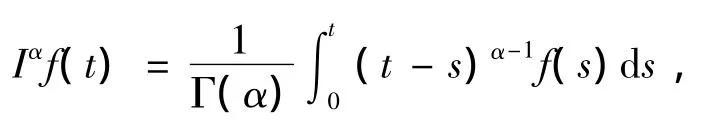
假定右端是在(0，∞)上逐点定义的.

定义3 函数f(t)，t＞0的Riemann-Liouville α(α＞0)阶分数次导数定义为

其中n=［α］+1，假定右端是在(0，∞)上逐点定义的.

引理1 设α＞0，则分数阶微分方程CDαu(t)=0有形如

u(t)=c0+c1t+c2t2+…+cn-1tn-1的解，其中ci∈R，i=0，1，2，…，n-1，n=［α］+1.

引理2 设α ＞0，则对于某些ci∈R，i=0，1，2，…，n-1，n= ［α］+1，有IαCDαu(t)=u(t)+c0+c1t+c2t2+… +cn-1tn-1.

引理3 设E是Banach空间X中闭的非空凸子集，F:E→E是连续映射且F(E)是X的相对紧致子集，则F在E中至少有1个不动点.

引理5 边值问题CDβ(CDα+λ)u(t)=f(t，u(t)，CDqu(t))，t∈［0，T］，1＜ α≤2，0＜ q＜ 1，α-q≥1，0＜β≤1的解为

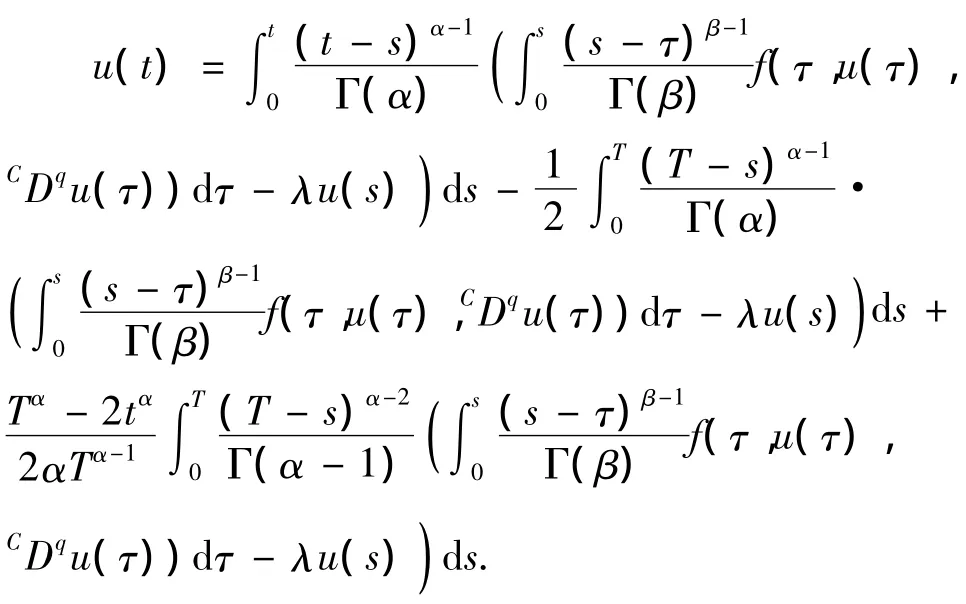
证 证明过程与文献［4］的(1.5)相类似，此处略.

2 主要结果

本节主要讨论问题(2)解的存在性.设J=［0，T］和C(J)是所有定义在J上连续实函数构成的空间.定义空间X={x(t)∈C(J)}且赋予范数‖x‖=(其中0＜q＜1).显然，(X，‖·‖)是 Banach空间.

定理1 设f:J×R×R→R是连续函数.假定存在1个常数l∈(0，β］和1个实值函数m(t)∈L1/l(［0，T］，(0，∞))(l ＞ 1)使得，其中 d1，d2≥ 0，0≤ρ1，ρ2＜1，则问题(2)在［0，T］至少有1个解.

证根据引理3，问题(2)等价于如下积分方程:

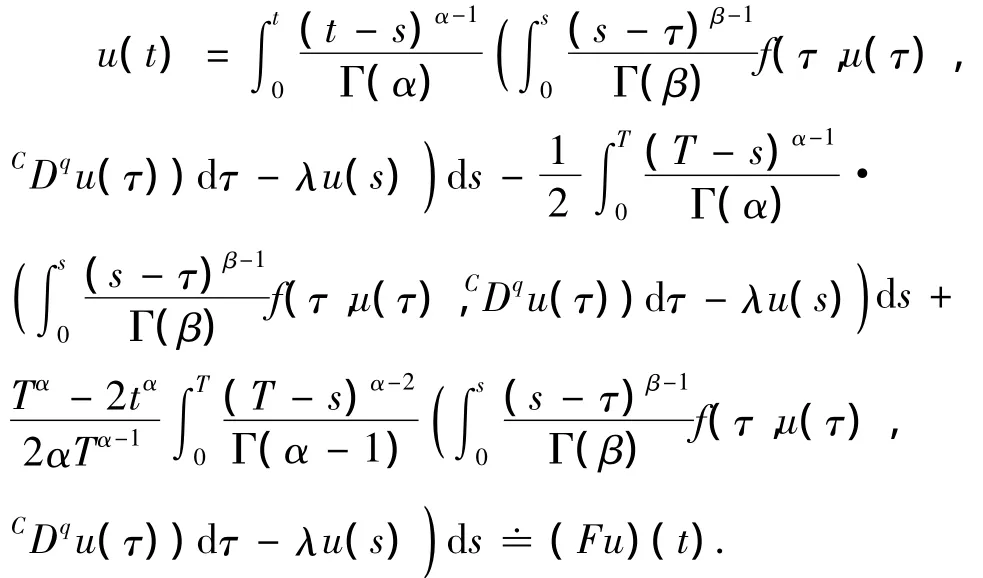
定义 Br={u(t)∈ X，‖u‖≤r，t∈ J}，则‖CDqu(t)‖≤r，其中

注意到Br是Banach空间X的1个有界闭凸子集.∀x∈Br，由引理4(Hölder不等式)得

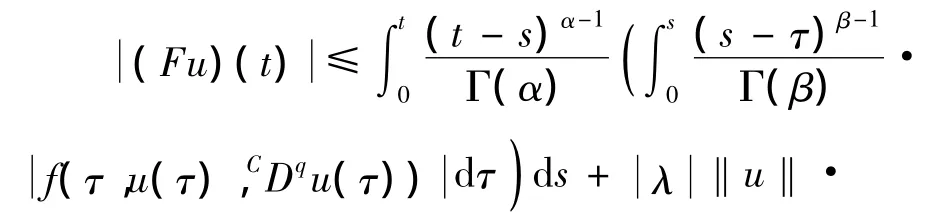
注意到Beta函数的性质:

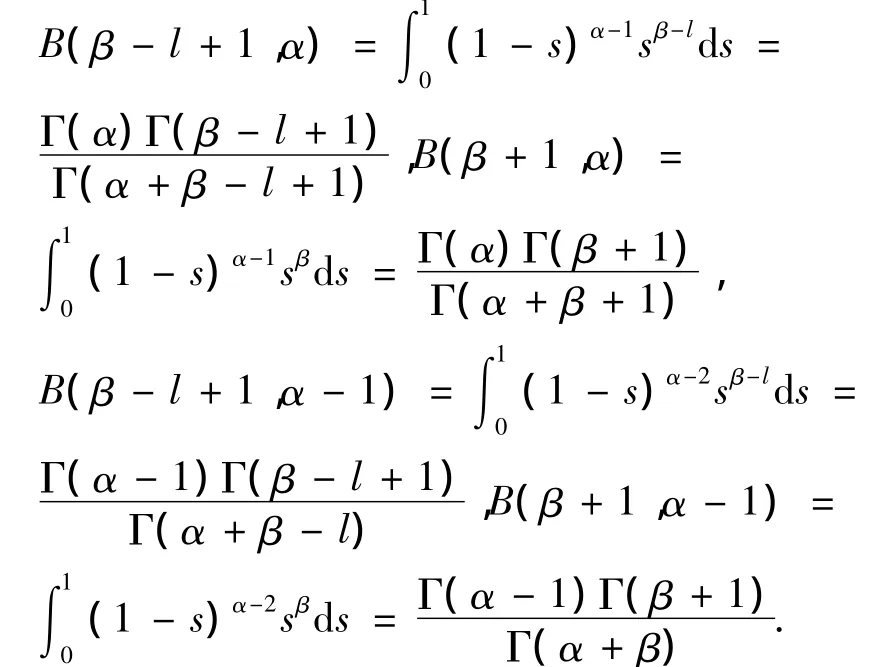
从而

对于每个x∈Br，将证明如果t1，t2∈J，且0＜t2-t1＜ δ，那么‖(Fu)(t2)-(Fu)(t1)‖＜ε.

事实上，

由平均值定理和(4)式得

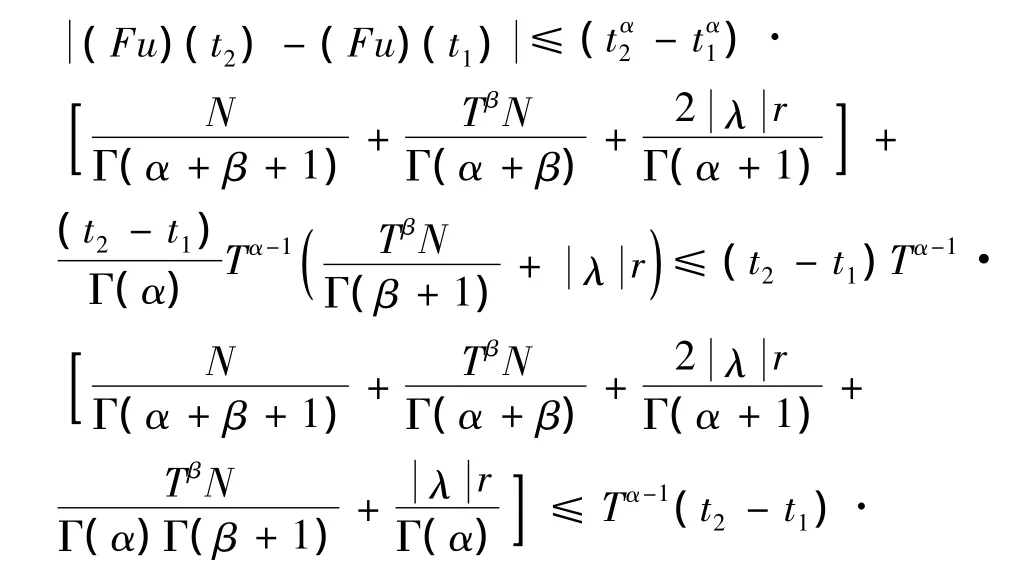
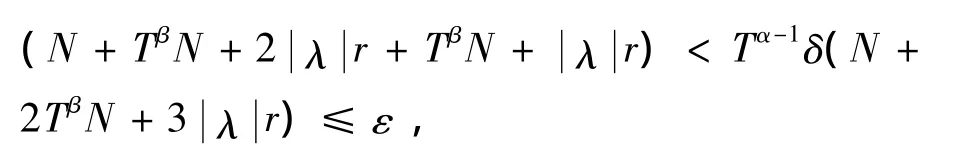
故有‖(Fu)(t2)-(Fu)(t1)‖＜ε.

因此，F是同等连续和一致有界的.由Arzela-Ascoli定理可知F在Br上是紧致的，故算子F是全连续的.于是算子F满足引理3的条件，由引理3知反周期边界值问题(2)在［0，T］上至少有1个解.

3 结论与展望

本文主要利用Schauder不动点定理、微积分中值定理和Hölder不等式等方法研究了一类非线性分数阶微分方程(2)有解的1个充分条件.在今后的研究中将讨论解的唯一性，从而为这类微分方程的数值解的计算奠定理论基础.

［1］ PodlubnyI.Fractional differential equations［M］.San Diego:Academic Press，1999.

［2］肖飞.一类分数次中立型发展方程的初值问题［J］.江西师范大学学报:自然科学版，2013，37(5):466-470.

［3］Cernea，A.On the existence of solutions for fractional differential inclusions with anti-periodic boundary conditions［J］.JAppl Math Comput，2012，38(1/2):133-143.

［4］KhuriAI.Advanced calculus with applications in statistics［M］.NewYork:Wiley，1993.

［5］ChenAnping，Chen Yi.Existence of solutions to anti-periodic boundary value problem for nonlinear fractional differential equations ［J］.Differ Equ Dyn Syst，2011，19(3):237-252.

［6］ChenAnping，Chen Yi.Existence of solutions to nonlinear Langevin equation involving two fractional orders with boundary value conditions［J］.BoundaryValue Problems，2011(1):1-17.

［7］Wang Fang，Liu Zhenhai.Anti-periodic fractional boundary value problems for nonlinear differential equations of fractional order［J］.Adv Diff Equ，2012，116:385-391.

［8］Bai Zhanbing，Lu Haishen.Positive solutions for boundary value problem of nonlinear fractional differential equation［J］.J MathAnalAppl，2005，311(2):495-505.

［9］Li Chengfu，Luo Xiannan，Zhou Yong.Existence of positive solutions of the boundary value problem for nonlinear fractional differential equations［J］.Computers＆ Mathematics withApplications，2010，59(3):1363-1375.

［10］周宗福，贾宝瑞.分数阶微分方程反周期边值问题解的存在性［J］.安徽大学学报:自然科学版，2011，35(1):1-4.

［11］ Zhang Shuqin.Positive solutions for boundary-value problems of nonlinear fractional differential equations［J］.Electronic Journal of Differential Equations，2006(36):1-12.

［12］周燕，张毅.基于Caputo导数的分数阶Pfaff-Birkhoff原理和Birkhoff方程［J］.江西师范大学学报:自然科学版，2014，38(2):153-157.

［13］LaksmikanthamV，Leela S.Nagumo-type uniqueness result for fractional differential equations ［J］.NonlinearAnal，2009，71(7/8):2886-2889.

［14］全晓静，韩惠丽，王健.Adomian分解法求解非线性分数阶Volterra积分方程［J］.江西师范大学学报;自然科学版，2014，38(5):517-520.

［15］刘青霞，刘发旺.二维分数阶变系数对流-扩散方程的数值解［J］.高等学校计算数学学报，2011，33(1):81-89.

［16］薛亚栋，冯春华.一类时滞脉冲微积分方程的正概周期解［J］.广西师范大学学报:自然科学版，2012，30(4):48-53.