The Toeplitz Operators on the Weighted Banach Space of theUnit Ball

YANG Xiang-dong

(Department of Mathematics，KunmingUniversity of Science and Technology，Kunming Yunnan 650093，China)

0 Introduction and Results

For any integer n≥1，let Cndenote the Cartesian product of n copies of C.For z=(z1，…，zn)and ζ=(ζ1，…，ζn)in Cn，the inner product is defined by，and throughout this paper，we denote.Moreover，Βnstands for the open unit ball which consists of all z in Cnwith

Let dv denote the normalized volumemeasure on Βn(i.e.，v(Βn)=1).It is well known that，for a real parameter α，

holds if and only if α＞-1.We denote

whereaαis some positive constant satisfying vα(Βn)=1 with some fixed α＞-1.

By Lpwe denote the space of p integrable functions on Βnwith respect to themeasure dvα.Here 1≤p≤∞.The Bergman spaceis the closed subspace ofLpwhich consists ofallanalytic functions.The normalized reproducing kernels forare of the form

The orthogonal projection P:L2→is defined by the following integral operator

The Toeplitz operator on L2awith symbol φ ∈ L1is defined by

The Berezin transform of a function φ ∈ L1is defined by

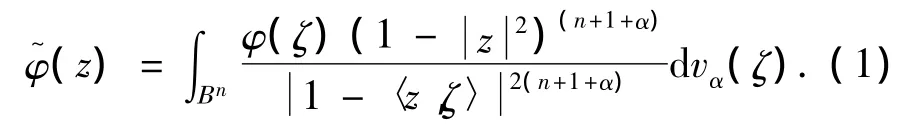
Since the Bergman projection can be extended to L1，the operator Tφis well defined on Η∞(Βn)，the space of bounded analytic functions on Βn，which is dense in.Hence，Tφis always densely defined on.

For the case of bounded symmetric domains，the boundedness and compactness of Toeplitz operators on Bergman spaces were characterized in terms of Berezin transform in［1］.The Berezin transform was employed tomake a study of Toeplitz operators onBergman spaces of the unit ball in［2］.

Recently，there arose an interest in studying operators on weighted Banach spaces of analytic functions.Motivated by ［1-2，3-8］in this paper，in terms of Berezin transform，we will characterize the continuity and compactness of the Toeplitz operators on the weighted Banach space HUofanalytic functions on the unit ball.Denote

From ［9-11］we know that the spaceis not only a(LB)-space，i.e.，countable inductive limit of Banach spaces，but also a complete space.More precisely，the topology could be defined bymeans of the family of weighted sup-seminorms

whereU is the set of all continuous，positive，radial functions u:Βn→ R such that for allm

The continuity and compactness of Toeplitz operators inare characterized in terms of the growth properties ofthe Berezin transform as follows.

Theorem 1Let φ be a nonnegative function defined on Βn.Then the Toeplitz operator Tφ:→is continuious if and only if there some k0andA＞0 such that the Berezin transformin(1)satisfies

where w(z)is defined in(2).

Theorem 2Let φ be a nonnegative function defined on Βn.Then the Toeplitz operator Tφ:→is compact if there exist some k0such that for every positivem，there existsAk＞ 0 with

Ak(w(z))k0，z∈ Βn，

where w(z)is defined in(2).

1 Preliminaries

For z∈ Βn，let ψzbe the analyticmap of Βnonto Βnsuch that ψz(0)=z and ψz◦ψz(w)=w.Thesemaps ψzare called involutions of Βn.For example，in the case of the unit disk，

is such amap.

The Bergmanmetric on the unit ball is given by

For any z∈Βnand r＞0 denote the Bergmanmetric ball by

And it is well-known that once r is fixed，then the volume vα(D(z，r))is comparable to(1-［11］for example.

An r-lattice in the Bergmanmetric is a sequence{ak}in Βnsatisfying the following conditions(see［2］for example)

(i)The unit ball is covered by the Bergmanmetric balls{D(ak，r)};

(ii)β(ai，aj)≥ r/2 for all i and j with i≠ j.

Throughout this paper，we will denote positive constants byA and itmay be different at each occurrence.

We shall use the following lemma(see ［11］and［2］for example)..

Lemma 1Suppose that b is an arbitrary real number and r＞0.Then there is a positive constantA such that

for all z，ξ andη in Βnwith β(ξ，η)≤r.

As a consequence，if r ＞0 andA is some positive constant，then the following inequality

holds for all z，ξ andη in Βnwith β(ξ，η)≤r.

Remark 1Let F and G be positive real valued functions.The symbol F ≅ G will be used，if there exist two absolute，positive constantsA1andA2such thatA1F≤G≤A2F holds on the whole domain of definition.From(5)，it is clear that

wherever z，ξ andη in Βnwith β(ξ，η)≤r.

We shall present some results on the spacefor later use.Let w(z)be defined in(2).And wedefine

Lemma 2(i)If u ∈U，then the pointwise product wkv also belongs toU;

(ii)Themapping P is a continuious projection fromto;

We also collect some results on linear operators from［8-9］in the following lemma for later use.

Lemma 3(i)A linear operator between two(LB)-spaces is continuous if and only if itmaps bounded sets into bounded sets.In the case of this paper thismeans that Tφ：→is continuous if and only if for everym∈N one can findAm＞0 and some exist some k0such that Tφ(Um)⊂AmUm+k0;

(ii)ThelinearoperatorTφ:→is compact if and only if there exists some k0such that for everym，one can findAm＞ 0 and such that Tφ(Um)⊂AmUk0.

2 Proof of Theorem

Proof of Theorem 1Our proof follows from a combination of themethods and constructions in［8］and ［2］.Let{ak}be a r-lattice which satisfiesand 1-2-(k-1)＜r≤1-2-k.since φ(ζ)is a positive symbol，combitination of the definition of Berezin transform in(1)and(4)yields.

By Lemma 1，we have

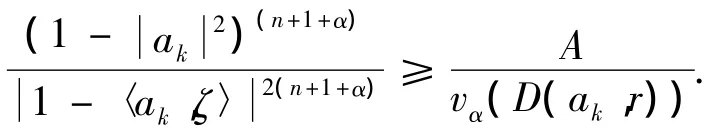
Since vα(D(ak，r))is comparable to，we have

From Lemma 3，it is clear that the continuity of Tφfollows if for an arbitrarym∈N we can find a constantAm，k0＞ 0 such that Tφ(Um)⊂Am，k0Um+k0+1.

To prove these facts，we fix the r-lattice{ak}in the Bergmanmetric as the beginning of the proof and estimate Tφas follows.Without loss of generality，wemay assume zN=1-2-N，then

For ζ∈ D(ak，r)，we have2-N)(1-2-k)≅ 2-N+2-k.Since f∈Um，we have the following estimate

By(8)and(9)，(7)can be bounded by a constant times

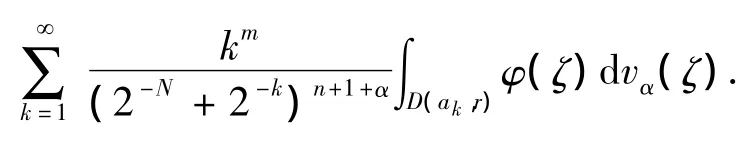
Combination of these estimates and(6)yield

Now we proceed with the estimate of the series

We write the series on the right side of(11)as

It is easy to derive the following inequality

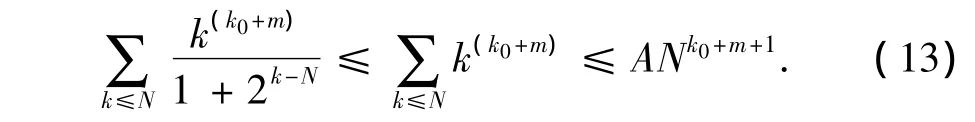
Integrating byparts theexpressionyields

By(10)～(14)，we get the estimate≤ANk0+m+1≤A'which shows that TφmapsUmintoUk0+m+1.Thus the continuity of Tφis proved.

Conversely，if Tφis bounded.we can find k0∈N such that TφmapsU1intoAUk0.For every z∈ Βn，we have

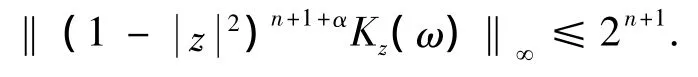
Thus，Tφ((1-)n+1+αKz(ω))∈ 2n+1+αAUk0forevery z and

holds for all ζ∈ Βn.Taking ω=z，we get

Proof of Theorem 2Since the proof is the same to the proof of Theorem 1，we just need to give a sketch of the proof here.

Let{ak}be a r-lattice which satisfies1-2-kand 1-2k-1＜r≤1-2-k.Applying the same reasoning of(6)，with≅k included，we have

From Lemma 3，it is clear that the compactness of Tφfollows if we can show that there existsm0∈N such that for everym∈N one can findAm＞0 and such that Tφ(Um)⊂AmUm0.

To prove these facts，we fix the r-lattice{ak}in the Bergmanmetric as the beginning of the proof and estimate Tφas follows.Without loss of generalization，wemay assume zN=1-2-N，replacing(6)by(15)，then applying the reasoning of(7)～(14)，we have the estimate which shows that TφmapsUmintoUk0+1.Thus the compactness of Tφis proved.

［1］ Zhu Kehe.Positive toeplitz operators on weighted bergman spaces of bounded symmetric domains［J］.J Operator Theory，1988，20(2):329-357.

［2］ Zhu Kehe.Schatten class toeplitz operators on weighted bergman spaces of the unit ball［J］.New York J Math，2007，13:299-316.

［3］Zhu Kehe.Operator theory in function spaces［M］.New York:Marcel Dekker，1990.

［4］Berger CA，Coburn LA.Toeplitz operators and quantummechanics［J］.J FunctAnal，1986，68(3):273-299.

［5］Berger CA，Coburn LA.Toeplitz operators on the Segal-Bargmann space ［J］.TransAmer Math Soc，1987，301(2):813-829.

［6］Berger CA，Coburn LA.Heat flow and Berezin-Toeplitz estimates［J］.Amer J Math，1994，116(3):563-590.

［7］Berger CA，Coburn LA，Zhu Kehe.Toeplitz operators and function theory in n-dimensions［J］.Lecture Notes in Math，1987，1256:28-35.

［8］Bonet J，Taskinen J.Toeplitz operators on the space of analytic functions withlogarithmic growth ［J］.J MathAnalAppl，2009，353(1):428-435.

［9］Kothe G.Topological vector spacesI andII［M］.Berlin:Springer-Verlag，1979.

［10］Rudin W.Function theory in the unit ball of Cn［M］.New York:Springer-Verlag，1980.

［11］Zhu Kehe.Spaces of holomorphic functions in the unit ball［M］.New York:Springer-Verlag，2005.