信息区间删失数据的参数估计及敏感性分析

李文静，邓文丽，章婷婷

(江西师范大学数学与信息科学学院，江西南昌330022)

0 引言

在临床实验或医学研究中，由于客观因素的限制，失效时间常常不能直接观测到，而只能知道它在某一个区间内，这类数据在统计学上被称为区间删失数据(interval-censored data).如在一些传染性疾病感染时间的研究中，实验对象被放入传染源后，只能知道在某个观察点实验对象是否已染上疾病，染上疾病的具体时间却无法观测到，所以只能推测出从接触传染源到染上传染病所经历的时间落在某个区间内.

区间删失数据存在于许多应用领域中，因此，这引发了一些统计学者对相关问题的研究.Huang Jian等［1］对区间删失数据的分类及对应的统计方法进行了较为详细地描述.Sun Jian-guo［2］较为全面和系统地概括了区间删失数据分析中涉及到的基本概念和方法.吕秋萍等［3］运用无偏转换思想构造了区间删失数据函数的均值估计，并在此基础上对所构造的估计量方差进行了研究.在区间删失数据的研究中，许多学者都是基于失效时间变量T和删失时间变量C相互独立的假定进行研究的，称这种删失情况为独立删失或非信息删失(Independent Censoring，Noninformative Censoring).然而，在实际问题中，这个假定常常会遭到质疑.如在对某种疾病的治疗中，由于病情恶化或者是已接受的治疗方案不奏效，从而导致病人退出治疗，这种情况通常预示着该病人的存活时间会比较短，即删失的个体对应的生存时间更短.相反地，有些病人的退出可能因为病情好转，不需要进一步治疗，这种情况的删失个体的生存时间可能会较长.和独立删失相反的是非独立删失(Dependent Censoring)，或称为信息删失(Informative Censoring).如果对信息删失数据仍采用独立删失下的统计分析方法，则可能会得到有偏或者无效的结论.

在信息删失数据的研究中，对失效时间和删失时间相依性的假定是至关重要的.正确的假定可以提高估计的效率，得到更好的统计结论;不合适的假定可能会导致错误的结论.在实际应用中，由于造成信息删失的应用背景和原因的不同，失效时间和删失时间相依的形式和程度也变得非常复杂，很难准确估计.敏感性分析可以评价相依关系的假定对统计分析结果造成的影响.王纯杰［4］基于Copula函数的一些性质，给出了非参数模型下的信息区间删失数据分布函数的相合估计.F.Siannis等［5］对失效时间和删失时间的相依关系进行了假定，引入了标示相关程度的参数和偏度函数，且对参数估计受相依程序的影响进行了敏感性分析.Y.Park等［6］在单个总体和2个总体的情形下，分别对独立删失和信息右删失混合数据下的相关估计问题进行了敏感性分析.Zhang Zhi-gang等［7］在正态脆弱模型假定下对I型信息区间删失数据的比例风险模型进行了敏感性分析.Huang Xue-lin等［8］基于连接函数(Copula)对信息右删失数据下的比例风险模型的估计问题进行了敏感性分析.

本文拟基于连接函数对信息区间删失数据下失效时间的生存函数进行估计，并在3种不同连接函数的情形下关于相依关系对参数估计所造成的影响进行敏感性分析.

1 方法

记Ti为第i个个体的失效时间，Ci为第i个个体的删失时间.试验中得到的独立同分布观测值为{(ci，δi)，i=1，2，…，n}，其中

假设Ti和Ci的边际分布函数分别为F(·)和G(·)，g(·)是Ci的边际密度函数，这里i=1，2，…，n.

基于观测样本，可以构造似然函数:

当Ti和Ci相互独立时，基于观测样本的似然函数为

当Ti和Ci不相互独立时，给定1个有参数α的连接函数H(u，v，α)，假设 Ti和 Ci的联合分布函数为J(t，c)=P(Ti≤t，Ci≤c)=H(F(t)，G(c)，α)，联合生存函数为

S(t，c)=P(Ti＞ t，Ci＞ c)=1-F(t)-

G(c)H(F(t)，G(c))，

则第i个个体被删失的概率为

同理可得，第i个个体失效的概率为

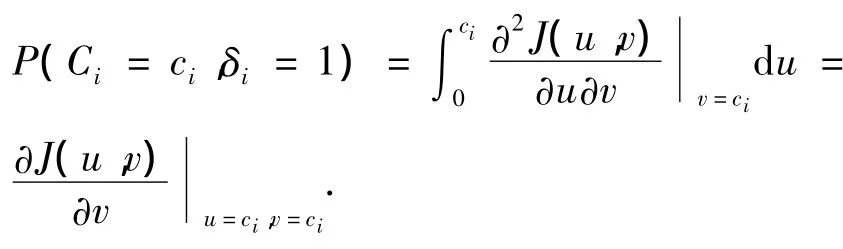
由此可知，

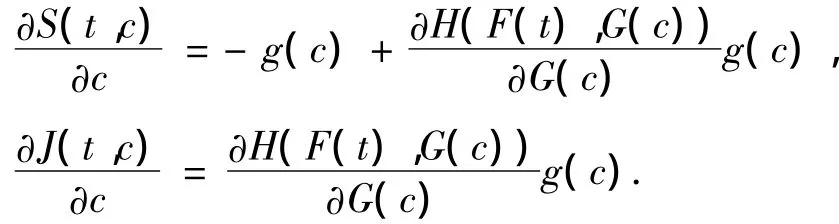
综上所述，当失效时间和删失时间不相互独立时，样本的观测似然函数可以表示为

在信息区间删失数据中，删失时间能够完全观测到，所以G(·)可以直接用它的经验分布函数代替，其中

似然函数(1)可以转化为

如果对失效时间的分布形式掌握的信息不多，则通常会考虑用非参数模型直接估计失效时间的分布函数.类似于文献［2］给出的独立区间删失数据非参数极大似然估计的方法，可以在(2)式中利用邓文丽等［9］提出的一类保序最优化问题的迭代算法得到分布函数F的估计.当已知一些影响失效时间的协变量时，比例风险模型和加速失效模型是广泛接受的2类半参数模型.如果假定协变量的影响满足比例风险模型，则在似然函数的表达式中，边际分布函数F(·)可以用含回归系数和基准风险函数的分布函数表达式代替，然后在似然函数(2)中，通过迭代的方法得到相关的估计;如果假定协变量的影响满足加速失效模型，则在似然函数的表达式中，边际分布函数F(·)可以用含回归系数和随机误差项的分布函数表达式代替，然后在似然函数(2)中，通过迭代的方法得到相关的估计.张连增等［10］基于极大似然法研究了Copula的参数和半参数方法的估计效果.如果失效时间的分布函数形式已知，而只待估其中包含的参数，则利用似然函数(2)就可以得出参数的极大似然估计.

2 数值模拟

在实际应用中由于失效时间和删失时间相依的形式和程度非常复杂，很难准确估计，所以通过敏感性分析来评价相依关系的假定对统计分析结果造成的影响.

模拟计算中失效时间T采用威布尔分布随机生成，因为它的危险率不是常数，所以，与指数分布相比，它有较广阔的应用，将其用于调查深槽轮滚珠轴承的疲劳寿命，或将其用于描写电子管的失效.威布尔的分布函数为 F(t)=1-e-(λt)γ，其中，γ 是分布曲线的形状参数，λ是尺度参数.模拟计算中选取了γ=2，λ=0.5.删失时间C的边际分布选取的是(0，A)上的均匀分布，调整A的大小可以改变删失的比例.

失效时间和删失时间的相关性选用阿基米德连接函数来描述.这里选取了 Clayton、Gumbe-Hougard和Frank 3种连接函数.

D.G.Clayton［11］给出在 τ=1/(1+2α)下的Copula函数:

E.J.Gumbel等［12］给出 τ=1-1/α 下的Copula函数:

H(u，v，α)=exp{- ［(-log u)α+

(-log v)α］1/α}(α ≥ 1).

2.1.1 30 g/L甲基二磺隆对麦田禾本科杂草的防效经过药前杂草基数调查可知，试验药剂处理区、对照药剂处理区及空白处理区野燕麦发生基数为：17.92，18.83，20.42，20.83，20.25，19.83 株；雀麦的发生基数为：18.92，19.08，16.92，20.00，20.08，20.08 株。

M.J.Frank［13］给出的 Copula 函数:

H(u，v，α)=log{1+(αu-1)(αv-1)

(α -1)}(α ＞ 0，α ≠1)，其中τ=1+4γ-1［D1(γ)-1］，γ=-log α，D1(γ)=

R.B.Nelsen［14］对于连接函数的相关性质和特殊的连接函数进行了详细介绍.

下面主要是通过数值计算分析连接函数的选取对参数γ和λ的估计产生的影响.这里的稳健性分析包括参数敏感性分析和连接函数敏感性分析.

2.1 参数的敏感性分析

分别取 τ=0.8、τ=0.5、τ=0.2的 Frank Copula作为连接函数，T服从γ=2，λ=0.5的威布尔分布，C服从(0，37)上的均匀分布，生成容量为200的样本，删失比例P(T＜C)为0.5.在本文方法中，选取 Frank连接函数，τ=0.8.模拟次数为1000，得到上述情况下λ～和γ～的均值、标准差和偏差的估计值(见表1).

表1 总体的参数τ变化下参数γ和λ的估计

由表1可以看出:如果生成样本的Frank连接函数的参数τ为0.2、0.5、0.8，采用独立删失的估计方法，得到的γ和λ估计量的偏差都较大，特别是γ估计值的偏差很大.而采用本文方法(选取Frank连接函数，参数τ=0.8)得到的估计量都比较理想，其估计值的偏差远远小于独立删失下估计值的偏差.由此可见，在失效时间和删失时间不相互独立的情况下，采用独立删失方法进行估计会得到不理想的估计结果，因此，应该采用带相关性假定的模型进行分析.

2.2 改变连接函数下参数估计的敏感性分析

分别取Clayton Copula和Gumbel Copula作为连接函数，τ=0.8，T服从γ=2，λ=0.5的威布尔分布，C服从(0，37)上的均匀分布，生成容量为200的样本，删失比例P(T＜C)为0.5.在估计方法中采用Frank连接函数，τ=0.8.2种数据集下λ～和γ～的均值、标准差如表2所示.

表2 总体的连接函数形式变化时参数γ和λ的估计

由表2可以看出:当τ=0.8时，如果生成样本的连接函数分别选取Clayton和Gumbel连接函数，采用独立删失的估计方法，得到的γ和λ估计量的偏差都很大.而采用本文方法(选取Frank连接函数，参数τ=0.8)得到的估计量都比较理想，估计量的偏差比较小.由此可见，在失效时间和删失时间不相互独立的情况下，采用独立删失方法进行估计可能会得到不理想的估计，所以应该采用带相关性假定的模型进行分析.

其次，在连接函数的选取对估计量的影响方面，当连接函数的假定和总体不一致时本文方法能够得到较稳健的估计量.

2.3 不同删失比例下参数估计的敏感性分析

选取C服从均匀U(0，3.3)和U(0，4.0)，删失比例P(T＜C)分别为0.3、0.7.T服从γ=2，λ=0.5的威布尔分布，连接函数为Frank，τ=0.8，生成容量为200的数据集，估计不同数据集下λ～和γ～的均值、标准差，估计结果如表3所示.

表3 不同删失比例下参数γ和λ的估计

由表3可以看出:如果连接函数及其参数τ的假定都是正确的，则在不同的删失比例下，本文方法都能够得到较好的估计，但采用独立删失方法得到的估计却不理想.

综合上述模拟计算的结果，可以得出:1)本文方法的参数估计效果比独立删失方法的参数估计效果更好;2)由连接函数不能准确识别或者参数τ不能正确识别所导致的偏差小于由独立删失错误假设所引起的偏差;3)当连接函数或参数τ的假定发生偏差时，本文方法依然能够较稳健.

3 讨论

通过上面的敏感性分析，可以看出在带信息的删失数据下估计参数的标准差小于在独立情况下估计参数的标准差.且对于不同连接函数、相关系数以及删失比例，效果都较稳健.另外，除了假设分布函数为威布尔分布外，还关于对数正态、指数分布等分布函数作了估计，效果也较好.因此，文本提供的方法具有一定的实用价值.

本文的工作还有许多地方可以进一步深入地研究，如在本文方法的框架下，继续解决半参数模型的分布函数估计［15］;考虑有协变量影响下基于连接函数的带信息删失的非参数估计等.

［1］ Huang Jian，Wellner JA.Interval censored survival data:a review of recent progress［M］.New York:Springer-Verlag，1997:123-169.

［2］Sun Jianguo.The statistical analysis of interval-censored failure time data［M］.New York:Springer-Verlag，2006.

［3］吕秋萍，邓文丽.区间删失数据函数的均值估计［J］.江西师范大学学报:自然科学版，2011，35(1):96-100.

［4］王纯杰.基于Copula函数的相依删失数据的非参数统计推断［D］.长春:吉林大学，2012.

［5］Siannis F，Copas J，Lu Baobing.Sensitivity analysis for informative censoring in parametric survivalmodels［J］.Biostatistics，2005，6(1):77-91.

［6］ Park Y，Lee Jenwei.One-and two-sample nonparametric inference procedures in the presence of amixture of independent and dependent censoring［J］.Biostatistics，2006，7(2):252-267.

［7］Zhang Zhigang，Sun Liuquan，Sun Jianguo，et al.Regression analysis of failure time data with informative interval censoring［J］.Statistics in Medicine，2007，26(12):2533-2546.

［8］ Huang Xuelin，Zhang Nan.Regression survival analysis with an assumed copula for dependent censoring:a sensitivity analysis approach ［J］.Biometrics，2008，64(4):1090-1099.

［9］邓文丽，朱莹莹.一类保序最优化问题的迭代算法［J］.统计与决策，2011(14):10-11.

［10］张连增，胡祥.Copula的参数与半参数估计方法的比较［J］.统计研究，2012，31(2):91-95.

［11］Clayton D G.Amodel for association in bivariate life tables and its application in epidemiological studies of familial tendency in chronic disease incidence ［J］.Biometrika，1978，65(1):141-151.

［12］ Hougaard P.A class ofmultivariate failure time distributions［J］.Biometrika，1986，73(3):671-678.

［13］Frank M J.On the sumultaneous association of F(x，y)and x+y-F(X，Y)［J］.Aequationes Mathematicae，1979，21(41):37-38.

［14］Nelsen R B.An introduction to copulas［M］.2nd ed.New York:Springer-Verlag，2006.

［15］杨金英，赵培信.缺失数据下ρ～混合误差线性模型的参数估计［J］.西南大学学报:自然科学版，2012，34(9):35-37.